Curve fitting
Curve fitting is het construeren van een wiskundige functie die het best past bij een reeks gegevenspunten.
Curve fitting kan zowel interpolatie als afvlakking inhouden. Interpolatie vereist een exacte fit met de gegevens. Bij afvlakking wordt een "gladde" functie geconstrueerd, die bij benadering bij de gegevens past. Een verwant onderwerp is regressieanalyse, die meer gericht is op statistische gevolgtrekkingen, zoals hoeveel onzekerheid er is in een kromme die past bij gegevens die zijn waargenomen met willekeurige fouten.
Geëxtrapoleerde krommen kunnen worden gebruikt om gegevens te visualiseren, om waarden van een functie te raden wanneer geen gegevens beschikbaar zijn, en om de relaties tussen twee of meer variabelen samen te vatten. Extrapolatie verwijst naar het gebruik van een passende curve buiten het bereik van de waargenomen gegevens. Dit is onderhevig aan een zekere mate van onzekerheid, aangezien het zowel de methode voor het construeren van de curve als de waargenomen gegevens kan weerspiegelen.
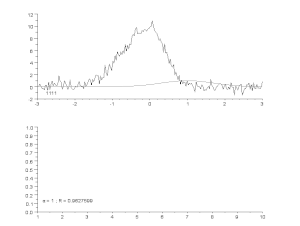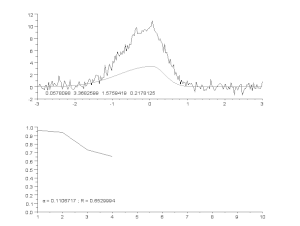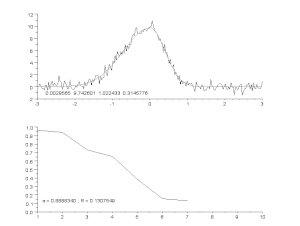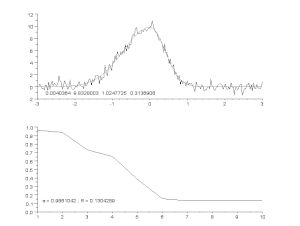
Fitting van een ruiscurve door een asymmetrisch piekmodel, met een iteratief proces (Gauss-Newton algoritme met variabele dempingsfactor α). Boven: ruwe gegevens en model. Onder: evolutie van de genormaliseerde som van de kwadraten van de fouten.
Vragen en antwoorden
V: Wat is curve fitting?
A: Curve fitting is het proces van het creëren van een wiskundige functie die het beste past bij een reeks gegevenspunten.
V: Wat zijn de twee soorten curve fitting?
A: De twee soorten curve fitting zijn interpolatie en afvlakking.
V: Wat is interpolatie?
A: Interpolatie is een type van curveaanpassing waarbij een exacte aanpassing aan de gegevens nodig is.
V: Wat is afvlakken?
A: Afvlakken is een vorm van curveaanpassing waarbij een "gladde" functie wordt geconstrueerd die ongeveer bij de gegevens past.
V: Wat is regressieanalyse?
A: Regressieanalyse is een verwant onderwerp dat zich richt op vraagstukken van statistische inferentie, zoals hoeveel onzekerheid er aanwezig is in een curve die past bij gegevens die met willekeurige fouten zijn waargenomen.
V: Wat zijn enkele toepassingen van gepaste krommen?
A: Gepaste krommen kunnen worden gebruikt om gegevens te visualiseren, waarden van een functie te raden wanneer er geen gegevens beschikbaar zijn, en relaties tussen twee of meer variabelen samen te vatten.
V: Wat is extrapolatie?
A: Extrapolatie is het gebruik van een gepaste curve buiten het bereik van de waargenomen gegevens. Dit is echter met een zekere mate van onzekerheid omgeven, aangezien het evenzeer de methode kan weerspiegelen die wordt gebruikt om de curve te construeren als de waargenomen gegevens.
Zoek in de encyclopedie