Functie (wiskunde)

In de wiskunde is een functie een wiskundig object dat een uitvoer produceert wanneer het een invoer krijgt (dat kan een getal zijn, een vector, of iets anders dat kan bestaan binnen een verzameling dingen).

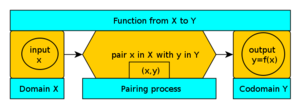
Een functie is dus als een machine, die een waarde van x neemt en een output y teruggeeft. De verzameling van alle waarden die x kan hebben heet het domein, en de verzameling die elke waarde bevat die y kan hebben heet het codomein. Een functie wordt vaak aangeduid met cursieve letters, zoals f {{displaystyle f} , g {displaystyle g} , h {displaystyle h} $h$ .

Als dit gebeurt, dan zeggen we dat y een functie van x is, en schrijven we y = f ( x ) $y=f(x)$ . Hier is f {f} de naam van de functie, en men schrijft f : X → Y {f:X naar Y} (functie van X naar Y) om de drie delen van de functie weer te geven: het domein (X), het codomain (Y), en het koppelingsproces (de pijl).

Een voorbeeld van een functie is f ( x ) = x + 1 {f(x)=x+1} $f(x)=x+1$ . Men geeft een natuurlijk getal x als invoer, en krijgt een natuurlijk getal y {displaystyle y} , wat x + 1 {displaystyle x+1} $x+1$ is. Bijvoorbeeld, als u 3 als invoer geeft aan f {displaystyle f} krijgt u 4 als resultaat.

Een functie hoeft geen vergelijking te zijn. Het belangrijkste idee is dat inputs en outputs op de een of andere manier aan elkaar worden gekoppeld - ook al is het proces misschien heel ingewikkeld.

Metaforen

Tabellen

De inputs en outputs kunnen in een tabel worden gezet zoals in de afbeelding; dit is gemakkelijk als er niet te veel gegevens zijn.

Grafieken

In de afbeelding kan men zien dat zowel 2 als 3 zijn gekoppeld aan c; dit is niet toegestaan in de andere richting, aangezien 2 niet tegelijkertijd c en d kan uitvoeren (elke invoer kan slechts één uitvoer hebben). Alle f ( x ) {\displaystyle f(x)} f(x) (c en d in de afbeelding) worden gewoonlijk de beeldverzameling van f {\displaystyle f} genoemd, en de beeldverzameling kan het gehele codomain zijn of een deelverzameling ervan. Men kan zeggen dat de beeldverzameling van een deelverzameling A van het domein f(A) is. Als de inputs en outputs een volgorde hebben, is het eenvoudig om ze in een grafiek uit te zetten:

Zo komt het beeld op het beeld van de verzameling A.

Geschiedenis

In de jaren 1690 gebruikten Gottfried Leibniz en Johann Bernoulli het woord "functie" in tussenletters, zodat het moderne begrip tegelijk met de calculus begon.

In 1748 gaf Leonhard Euler de volgende definitie van een functie:

"Een functie van een variabele grootheid is een analytische uitdrukking die op enigerlei wijze is samengesteld uit de variabele grootheid en getallen of constante grootheden."

en vervolgens in 1755:

"Als sommige grootheden zo afhankelijk zijn van andere grootheden dat als deze laatste worden veranderd, de eerste grootheden een verandering ondergaan, dan worden de eerste grootheden functies van de laatste genoemd. Deze definitie is tamelijk ruim van toepassing en omvat alle manieren waarop de ene grootheid door de andere kan worden bepaald. Als x dus staat voor een variabele grootheid, dan worden alle grootheden die op enigerlei wijze van x afhangen of daardoor worden bepaald, functies van x genoemd."

De eerste moderne definitie van een functie (geformuleerd in 1837) komt meestal van Peter Dirichlet. Hij wordt vaak gebruikt in scholen tot de tweede helft van de 20e eeuw:

"y is een functie van een variabele x, gedefinieerd op het interval a < x < b, indien met elke waarde van de variabele x in dit interval een welbepaalde waarde van de variabele y correspondeert. Ook is het niet relevant op welke wijze deze correspondentie tot stand komt."

In 1939 generaliseerde Bourbaki de definitie van Dirichlet, en gaf een set-theoretische versie van de definitie als een correspondentie tussen inputs en outputs; deze werd vanaf ongeveer 1960 op scholen gebruikt.

Uiteindelijk gaf Bourbaki in 1970 de moderne definitie als een drievoud f = ( X , Y , F ) {displaystyle f=(X,Y,F)} , met F ⊂ X × Y , ( x , f ( x )) ∈ $F\subset X\times Y,(x,f(x))\in F$ (d.w.z. f : X → Y {displaystyle f:X tot Y} en F = { ( x , f ( x )) ∣ x ∈ X , f ( x ) ∈ $F=\{(x,f(x))\mid x\in X,f(x)\in Y\}$ ). $X wordt$ het domein van $f$ genoemd, $Y$ het codomain, en $F$ de grafiek. De verzameling van alle elementen van de vorm $f (x)$ , waarbij $x$ reikt over de elementen van het domein $X$ , wordt het beeld van $f genoemd$ . Het beeld van een functie is een deelverzameling van zijn codomain en kan daarmee niet samenvallen.

Soorten functies

Elementaire functies - De functies die gewoonlijk op school worden bestudeerd: breuken, vierkantswortels, de sinus-, cosinus- en tangensfuncties en enkele andere functies.
Niet-elementaire functies - De meeste gebruiken bewerkingen die we niet op school leren (zoals + of -, of machten). Veel integralen, bijvoorbeeld, zijn niet-elementair.
Inverse functies - Functies die een andere functie ongedaan maken. Bijvoorbeeld: als F(x) de inverse is van f(x)=y, dan is F(y)=x. Niet alle functies hebben inverse functies.
Speciale functies: Functies die namen hebben. Hieronder vallen goniometrische functies zoals sinus, cosinus en tangens. Functies als f(x)=3x (driemaal x) worden geen speciale functies genoemd. Speciale functies kunnen elementair, niet-elementair of invers zijn.

Gerelateerde pagina's

Constante functie
Continue functie
Functie samenstelling
Speciale functies

Gamma-functie
Matrixfunctie

Lineaire functie
Lucy Joan Slater - Britse wiskundige die onderzoek deed naar wiskundige functies
MATLAB, Wolfram Mathematica - software om wiskundige functies te berekenen
Relatie (wiskunde)

Vragen en antwoorden

V: Wat is een functie in de wiskunde?

A: Een functie in de wiskunde is een object dat een uitgang produceert wanneer het een ingang krijgt, wat een getal, vector of iets anders kan zijn dat binnen een verzameling kan bestaan.

V: Wat zijn de twee verzamelingen die bij functies horen?

A: De verzameling van alle waarden die x kan hebben heet het domein en de verzameling die elke waarde bevat die y kan hebben heet het codomein.

V: Hoe worden functies vaak aangeduid?

A: Functies worden vaak aangeduid met cursieve letters zoals f, g, h.

V: Hoe stellen wij een functie voor?

A: Wij stellen een functie voor door y = f(x) te schrijven, waarbij f de naam van de functie is en men f : X → Y (functie van X naar Y) schrijft om de drie delen van de functie weer te geven - domein (X), codomain (Y) en koppelingsproces (de pijl).

V: Kunt u een voorbeeld geven van een functie?

A: Een voorbeeld van een functie is f(x) = x + 1. Men geeft een natuurlijk getal x als invoer en krijgt een natuurlijk getal y dat x + 1 is. Als men bijvoorbeeld 3 als input geeft aan f, krijgt men als output 4.

V: Moet elke functie een vergelijking zijn?

A: Nee, niet elke functie hoeft een vergelijking te zijn. Het belangrijkste idee achter functies is dat invoer en uitvoer op de een of andere manier aan elkaar worden gekoppeld - ook al is dat misschien heel ingewikkeld.