Balkvergelijking van Euler-Bernoulli
De Euler-Bernoulli straaltheorie (ook wel ingenieurstraaltheorie of klassieke straaltheorie genoemd) is een eenvoudige methode om de buiging van balken te berekenen wanneer een belasting wordt uitgeoefend. Zij is van toepassing op kleine doorbuigingen (hoe ver iets beweegt) van een balk zonder rekening te houden met effecten van afschuivingsvervormingen. Daarom kan zij worden beschouwd als een speciaal geval van de Timoshenko-balkenleer. De theorie werd voor het eerst rond 1750 geïntroduceerd. Zij won aan populariteit tijdens de ontwikkeling van de Eiffeltoren en het reuzenrad aan het eind van de 19e eeuw. Daarna werd zij gebruikt op vele gebieden van de techniek, waaronder de werktuigbouwkunde en de weg- en waterbouw. Hoewel er andere geavanceerde methoden zijn ontwikkeld, wordt de Euler-Bernoulli straaltheorie nog steeds veel gebruikt vanwege haar eenvoud.
Een trillende glazen balk toont de buiging van balken die kan worden geschat met behulp van de balkentheorie van Euler-Bernoulli.
Geschiedenis
Leonhard Euler en Daniel Bernoulli waren de eersten die de theorie in 1750 samenstelden. In die tijd werden wetenschap en techniek anders bekeken dan tegenwoordig. Wiskundige theorieën zoals de Euler-Bernoulli Beam theorie werden niet vertrouwd voor praktisch ingenieursgebruik. Bruggen en gebouwen werden nog steeds volgens dezelfde methoden ontworpen tot het einde van de 19e eeuw. Toen toonden de Eiffeltoren en het reuzenrad de geldigheid van de theorie op grotere schaal aan.
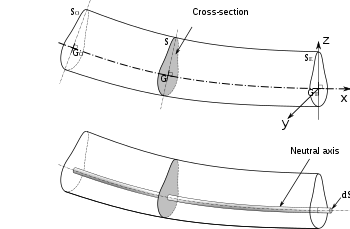
Tekening van een dwarsdoorsnede van een gebogen balk met aanduiding van de neutrale as
Statische straalvergelijking
De vergelijking van Euler-Bernoulli beschrijft het verband tussen de doorbuiging van de balk en de uitgeoefende belasting, zoals hieronder is aangegeven:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d}} ^{2}}{\mathrm {d} x^{2}}} links(EI{\frac {\mathrm {d}} ^{2}w}{\mathrm {d} x^{2}}} rechts)=q,} 
Hierin beschrijft w ( x ) {(x)}
de doorbuiging van de balk in de 
z-richting op een bepaalde plaats x {(x)} 
. q {(q)} 
is een verdeelde belasting, met andere woorden een kracht per lengte-eenheid (analoog aan druk als een kracht per oppervlakte); deze kan een functie zijn van x {(x)} , w {(x)} , of andere variabelen. 
of andere variabelen.
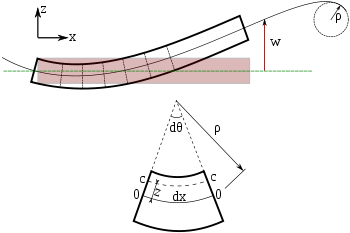
Doorbuiging van een Euler-Bernoulli balk. Elke doorsnede van de balk staat in een hoek van 90 graden ten opzichte van de neutrale as.
Vragen en antwoorden
V: Wat is de Euler-Bernoulli straaltheorie?
A: De Euler-Bernoulli balkentheorie is een eenvoudige methode om de buiging van balken bij belasting te berekenen, zonder rekening te houden met de effecten van dwarsvervormingen.
V: Wanneer werd de Euler-Bernoulli balkentheorie voor het eerst geïntroduceerd?
A: De Euler-Bernoulli balkentheorie werd rond 1750 geïntroduceerd.
V: Werd de Euler-Bernoulli balkentheorie gebruikt bij de ontwikkeling van de Eiffeltoren en het reuzenrad?
A: Ja, de Euler-Bernoulli balkentheorie werd populair bij de ontwikkeling van de Eiffeltoren en het reuzenrad aan het eind van de 19e eeuw.
V: Wat zijn enkele technische gebieden waarin de Euler-Bernoulli balkentheorie is gebruikt?
A: De Euler-Bernoulli balkentheorie is gebruikt in vele technische gebieden, waaronder werktuigbouwkunde en civiele techniek.
V: Wordt de Euler-Bernoulli balkentheorie vandaag de dag nog steeds veel gebruikt?
A: Ja, de Euler-Bernoulli balkentheorie wordt nog steeds veel gebruikt vanwege zijn eenvoud, ook al zijn er andere geavanceerde methoden ontwikkeld.
V: Op welke soorten doorbuigingen van een balk is de Euler-Bernoulli balkentheorie van toepassing?
A: De Euler-Bernoulli balkentheorie is van toepassing op kleine doorbuigingen van een balk.
V: Houdt de Euler-Bernoulli balkentheorie rekening met de effecten van dwarsvervormingen?
A: Nee, de Euler-Bernoulli balkentheorie houdt geen rekening met de effecten van dwarsvervormingen.
