Grafiek kleuren
Grafiekkleuring is de naam voor een aantal problemen uit de grafentheorie. Deze problemen betreffen het kleuren (of labelen) van de hoekpunten van een grafiek, gegeven bepaalde voorwaarden. Een eenvoudig probleem in deze context zou kunnen zoeken naar het minimale aantal kleuren dat nodig is om de hoekpunten te kleuren, wanneer twee verbonden hoekpunten niet dezelfde kleur kunnen hebben. In de afgebeelde grafiek worden de cirkels hoekpunten genoemd en de lijnen die ze verbinden randen. Het minimumaantal kleuren dat nodig is om een grafiek te kleuren wordt het chromatisch getal genoemd.
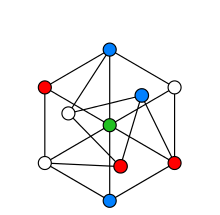
Een geldige oplossing voor het kleuren van een grafiek, wanneer twee verbonden hoekpunten niet dezelfde kleur mogen krijgen.
Vragen en antwoorden
V: Wat is grafiekkleuring?
A: Grafiekkleuring is een probleem uit de grafentheorie waarbij de hoekpunten van een grafiek worden gekleurd of gelabeld volgens bepaalde voorwaarden.
V: Wat is een eenvoudig probleem in de context van grafiekkleuring?
Antwoord: Een eenvoudig probleem kan zijn om het minimumaantal kleuren te vinden dat nodig is om de hoekpunten van een grafiek te kleuren, terwijl je ervoor zorgt dat twee verbonden hoekpunten niet dezelfde kleur hebben.
V: Hoe worden de cirkels in een grafiek genoemd?
Antwoord: De cirkels in een grafiek worden hoekpunten genoemd.
Vraag: Hoe worden de verbindingslijnen tussen de cirkels in een grafiek genoemd?
A: De lijnen die de cirkels in een grafiek verbinden worden randen genoemd.
V: Hoe heet het minimum aantal kleuren dat nodig is om een grafiek te kleuren?
A: Het minimum aantal kleuren dat nodig is om een grafiek te kleuren heet het chromatisch getal.
V: Wat is het doel van grafiekkleuring?
A: Het doel van grafiekkleuring is om oplossingen te vinden voor problemen in de grafiektheorie waarbij de hoekpunten van een grafiek gekleurd of gelabeld moeten worden volgens bepaalde voorwaarden.
V: Waarom is grafiekkleuring belangrijk?
A: Grafiekkleuring is belangrijk op verschillende gebieden, waaronder informatica, natuurkunde en sociale wetenschappen, en kan worden gebruikt om echte problemen te modelleren, zoals planning, toewijzing van middelen en netwerkoptimalisatie.
Zoek in de encyclopedie