Grafiektheorie
Grafiektheorie is een gebied van de wiskunde over grafieken. Een grafiek is een abstracte voorstelling van: een aantal punten die verbonden zijn door lijnen. Elk punt wordt gewoonlijk een hoekpunt genoemd (meerdere worden hoekpunten genoemd), en de lijnen worden randen genoemd. Grafieken zijn een hulpmiddel om relaties te modelleren. Ze worden gebruikt om antwoorden te vinden op een aantal problemen.
Enkele van deze vragen zijn:
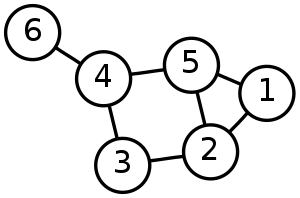
Een ongerichte grafiek.
Verschillende soorten grafieken
- Grafiektheorie heeft vele aspecten. Grafieken kunnen gericht of ongericht zijn. Een voorbeeld van een gerichte grafiek is het wegennet van een stad. Sommige straten in de stad zijn eenrichtingsstraten. Dit betekent, dat er op die stukken maar één richting te volgen is.
- Grafieken kunnen worden gewogen. Een voorbeeld is een wegennet, met afstanden, of met tol (voor wegen).
- De knooppunten (de cirkels in het schema) van een grafiek worden hoekpunten genoemd. De lijnen die de knooppunten verbinden worden randen genoemd. Er kan geen lijn zijn tussen twee knooppunten, er kan één lijn zijn, of er kunnen meerdere lijnen zijn.
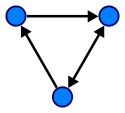
Een gerichte grafiek.
Geschiedenis
 →
→ →
→ 
Een visualisatie van de Zeven Bruggen van Königberg. Leonhard Euler loste dit probleem op in 1736, wat leidde tot de ontwikkeling van de topologie en de moderne grafentheorie.
Een grafiek is een abstracte gegevensstructuur. Het bevat knooppunten die gewoonlijk aan elkaar gerelateerd zijn. Een knooppunt is een dataset, meestal in de vorm van geordende paren. Knooppunten zijn al dan niet verbonden met een ander knooppunt. De relatie tussen knooppunten wordt meestal gedefinieerd als een Edge. Grafieken zijn nuttig omdat ze knooppunten kunnen verbinden met andere knooppunten. Er zijn een paar weergaven van Graphs in de praktijk.
Leonhard Euler woonde in de stad Königsberg. (De naam veranderde in 1946 in Kaliningrad). De stad ligt aan de rivier de Pregel. Er is een eiland in de rivier. Er zijn enkele bruggen over de rivier. Euler wilde rondlopen en elk van de bruggen een keer gebruiken. Hij vroeg of hij dit mocht doen. In 1736 publiceerde hij een wetenschappelijk artikel waarin hij aantoonde dat dit niet mogelijk was. Tegenwoordig staat dit probleem bekend als de Zeven Bruggen van Königsberg. Het artikel wordt gezien als het eerste artikel in de geschiedenis van de grafentheorie.
Dit artikel, evenals dat van Vandermonde over het ridderprobleem, zette de door Leibniz begonnen analyse situs voort. De formule van Euler over het aantal ribben, hoekpunten en vlakken van een convex veelvlak werd bestudeerd en veralgemeend door Cauchy en L'Huillier, en ligt aan de oorsprong van de topologie.
De fusie van de ideeën uit de wiskunde met die uit de chemie ligt aan de oorsprong van een deel van de standaardterminologie van de grafentheorie. Met name de term "grafiek" werd geïntroduceerd door Sylvester in een artikel dat in 1878 in Nature werd gepubliceerd.
Een van de beroemdste en productiefste problemen van de grafiektheorie is het vierkleurenprobleem: "Is het waar dat voor elke kaart die in het vlak wordt getekend, de gebieden met vier kleuren kunnen worden gekleurd, zodanig dat twee gebieden die een gemeenschappelijke grens hebben, verschillende kleuren hebben?".
.png)
Het probleem van de Königsbergbrug, op een stadsplattegrond
.png)
Hetzelfde probleem, maar dan met een grafiek
Grafiektheorie in perspectief
Grafiektheorie is een belangrijk onderdeel van de wiskunde en de informatica. Voor veel van deze problemen bestaan exacte oplossingen. Vaak zijn ze echter zeer moeilijk te berekenen. Daarom worden vaak benaderingen gebruikt. Er zijn twee soorten benaderingen: Monte-Carlo-algoritmen en Las-Vegas-algoritmen.
Vragen en antwoorden
V: Wat is grafiektheorie?
A: Grafentheorie is een tak van de wiskunde die grafieken bestudeert. Grafieken zijn abstracte voorstellingen van punten die door lijnen met elkaar verbonden zijn.
V: Hoe worden de punten in een grafiek genoemd?
A: De punten in een grafiek worden gewoonlijk hoekpunten genoemd.
V: Wat stellen de lijnen tussen de hoekpunten voor?
A: De lijnen tussen de hoekpunten stellen onderlinge relaties of verbindingen voor.
V: Hoe kunnen grafieken worden gebruikt?
A: Grafieken kunnen worden gebruikt om relaties te modelleren en antwoorden te vinden op verschillende problemen.
V: Wat voor soort vragen kunnen grafieken helpen beantwoorden?
A: Grafieken kunnen helpen bij het beantwoorden van vragen over netwerkanalyse, optimalisatie en planning.
V: Zijn er verschillende soorten grafieken?
A: Ja, er zijn verschillende soorten grafieken, zoals gerichte en ongerichte grafieken, gewogen en ongewogen grafieken, volledige en onvolledige grafieken, enz.
V: Is er software beschikbaar voor het werken met grafentheorie?
A: Ja, er is software beschikbaar voor het werken met grafentheorie, zoals Gephi en NetworkX.
Zoek in de encyclopedie