Ongelijkheid (wiskunde)

Werken met ongelijkheden

Ongelijkheid in de wiskunde is wanneer twee oplossingen of antwoorden met meer of minder worden vergeleken. Het is wanneer de twee of nog veel oplossingen worden vergeleken is niet van gelijke hoeveelheid. Het oplossen van een ongelijkheid betekent het vinden van oplossingen. Als je een getal vervangt door een variabele en de uitspraak is waar, dan is het een oplossing. Wanneer je een getal vervangt door een variabele en het statement is dan niet waar, dan is het getal geen oplossing voor het statement.

Ongelijkheid is het vinden van een oplossing voor een bepaalde variabele. Het is het vinden van een relatieve volgorde van een set. Ongelijkheid heeft veel oplossingen, maar je moet de echte oplossingen vinden. Ongelijkheid is het oplossen van echte getallen. De juiste manier om ongelijkheid af te lezen is van links naar rechts, net als de andere vergelijkingen, maar het enige verschil is dat ze verschillende regels hebben voor elke vergelijking.

Bijvoorbeeld, x+4>12, waarbij x een reëel getal is. Eerst moet een persoon de x vinden en hij/zij moet weten of het een oplossing is. Het antwoord zal x>8 zijn en het is een echte verklaring. Deze uitdrukking gaat over de plaats van x binnen de set van reële getallen. Een getallenlijn is een manier om de locatie ten opzichte van alle andere reële getallen te tonen (zie figuur Ongelijkheid 1).

Ongelijkheid 1 Dit is de oplossing voor de vergelijking x+4>12

Verschillende soorten ongelijkheden

Er zijn vijf verschillende soorten ongelijkheden:

1. De eerste is de lineaire ongelijkheid die een ongelijkheid is die de uitdrukkingen onderscheidt met minder of gelijk aan, minder of groter dan of gelijk aan, groter dan. Het is er een dat als we de ongelijkheid voor de gelijkenrelatie vervangen, dan zal de uitkomst een lineaire vergelijking zijn.
2. De tweede is de combinaties van de ongelijkheden die moeten voldoen aan de ongelijkheden, moet je een getal in de oplossing sets, zodat de getallen voldoen aan de ongelijkheden gaan de waarden in de kruising van de twee oplossingen sets zijn.
3. De derde is de ongelijkheid met betrekking tot absolute waarden, wat betekent dat de waarden kunnen worden geherformuleerd als combinaties van ongelijkheden die betrekking hebben op absolute waarden.
4. De vierde wordt polynomiale ongelijkheden genoemd, wat betekent dat ze continu zijn, het betekent dat hun grafieken geen sprongen of breuken hebben.
5. Last but not the least, is de rationele ongelijkheid, wat betekent dat het de vorm is van een van de polynomiale gedeeld door een polynomiale. Met andere woorden, de rationele functiegrafieken hebben geen breuken en staan ook niet voor de nullen van de noemer.

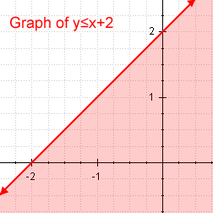
Lineaire ongelijkheid Voorbeeld van lineaire ongelijkheid


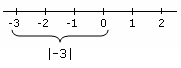
absolute waarde Voorbeeld dat een absolute waarde laat zien

Vier manieren om ongelijkheden op te lossen

Er zijn vier manieren om vierkantsvergelijkingen op te lossen:

1. Regel nummer één is dat je hetzelfde nummer aan beide zijden moet optellen of aftrekken.
2. Regel nummer twee is dat je de zijkanten moet verschuiven en de positie van het teken van de ongelijkheid moet veranderen.
3. Regel nummer drie is dat je moet vermenigvuldigen.
4. Regel nummer vier is om hetzelfde positieve of negatieve getal in beide zijden te verdelen. Maar, je kunt deze alleen gebruiken bij gemakkelijke ongelijkheidsproblemen.

Bovendien zal zij twee stappen ondernemen om een ongelijkheid op te lossen. De eerste stap is het vereenvoudigen van het gebruik van de wederkerige optelling of aftrekking. De tweede is om het gebruik van de reciproke van vermenigvuldiging of deling te vereenvoudigen. Wanneer je een ongelijkheid vermenigvuldigt of deelt met een negatief getal, vergeet dan niet het ongelijkheidssymbool te draaien.

Een voorbeeld van het toevoegen van ongelijkheden.


voorbeeld van vermenigvuldiging van de ongelijkheid

Voorbeelden van het oplossen van ongelijkheden

Ongelijkheid is een wiskundige uitspraak die verklaart dat de twee waarden niet gelijk en verschillend zijn. De vergelijking ab betekent dat a niet gelijk is aan b. Ongelijkheid is bij elke vergelijking gelijk, maar het enige verschil is dat de ongelijkheid geen gelijkteken gebruikt, maar dat er symbolen worden gebruikt. De ongelijkheid b>a betekent dat b groter is dan a. Snelheidslimieten,-markering, en andere gebruiken ongelijkheid om ze uit te drukken.

Bij het oplossen van een ongelijkheid moet een persoon een echte verklaring hebben. Wanneer je een ongelijkheid deelt of vermenigvuldigt met een negatief getal aan beide zijden is de uitspraak vals. Om de uitspraak correct te maken met een negatief getal moet je het symbool omkeren om die uitspraak correct te maken. Wanneer een getal een positief getal is, hoeft u het symbool niet om te keren. Ongelijkheid gaat over het maken van een echte uitspraak.

Begin bijvoorbeeld met een echte verklaring -6y<-12. Wanneer beide zijden gedeeld worden door -6 wordt het resultaat y< 2. In deze uitspraak moet het symbool omgedraaid worden om een ware uitspraak te hebben, y>2 is het juiste antwoord. In de getallenlijn (zie figuur Ongelijkheid 2) wijst een gesloten gearceerde cirkel erop dat deze is opgenomen in de oplossingenset. Een open cirkel geeft aan dat deze niet in de oplossingenset is opgenomen.

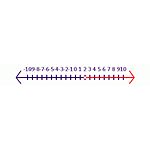
Ongelijkheid 2 Oplossing voor de vergelijking -6y<-12

Gerelateerde pagina's

• Gelijkheid (wiskunde)
• Vergelijking