Minkowski-ruimte | een vierdimensionale manifold, gecreëerd door Hermann Minkowski
In de speciale relativiteit is de Minkowski-ruimtetijd een vierdimensionale manifold, gecreëerd door Hermann Minkowski. Hij heeft vier dimensies: drie dimensies ruimte (x, y, z) en één dimensie tijd. De Minkowski-ruimtetijd heeft een metrische signatuur van (-++), en beschrijft een plat vlak wanneer er geen massa aanwezig is. De conventie in dit artikel is om Minkowski-ruimtetijd gewoon ruimtetijd te noemen.
De Minkowski-ruimtetijd is echter alleen van toepassing in de speciale relativiteit. De algemene relativiteit gebruikte het begrip gekromde ruimtetijd om de effecten van zwaartekracht en versnelde beweging te beschrijven.
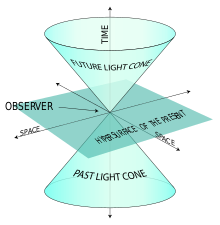
Voorbeeld van een lichtkegel.
Definitie(s)
Wiskundig
Ruimtetijd kan worden beschouwd als een vierdimensionaal coördinatenstelsel waarin de assen worden gegeven door
Ze kunnen ook worden aangeduid met
Waarbij 

Dit impliceert dat ruimtetijd een metrische tensor heeft gegeven door
Zoals eerder gezegd, is ruimtetijd overal vlak; tot op zekere hoogte kan hij worden beschouwd als een vlak.
Eenvoudig
Ruimtetijd kan worden beschouwd als de "arena" waarin alle gebeurtenissen in het universum plaatsvinden. Alles wat men nodig heeft om een punt in de ruimtetijd te specificeren is een bepaalde tijd en een typische ruimtelijke oriëntatie. Het is moeilijk (vrijwel onmogelijk) om vier dimensies te visualiseren, maar met onderstaande methode kan enige analogie worden gemaakt.
Ruimtetijd diagrammen
Hermann Minkowski introduceerde een bepaalde methode voor de grafiek van coördinatenstelsels in de Minkowski-ruimtetijd. Zoals u hiernaast kunt zien, zullen verschillende coördinatensystemen het oneens zijn over de ruimtelijke oriëntatie en/of de positie van een object in de tijd. Zoals u in het diagram kunt zien, is er slechts één ruimtelijke as (de x-as) en één tijdas (de ct-as). Indien nodig kan men een extra ruimtelijke dimensie invoeren (de y-as); helaas is dit de limiet van het aantal dimensies: grafieken in vier dimensies zijn onmogelijk. De regel voor grafieken in Minkowski-ruimtetijd gaat als volgt:
1) De hoek tussen de x-as en de x'-as wordt gegeven door 
2) De lichtsnelheid door ruimtetijd maakt altijd een hoek van 45 graden met een van beide assen.
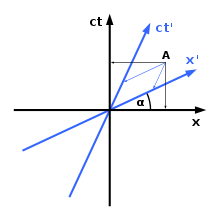
In de relativiteitstheorie wijzen beide waarnemers de gebeurtenis bij A toe aan verschillende tijden.
Ruimtetijd in algemene relativiteit
In de algemene relativiteitstheorie gebruikte Einstein de vergelijking
Om de ruimtetijd daadwerkelijk te laten krommen; de resulterende effecten zijn die van de zwaartekracht.
Gerelateerde pagina's
- Ruimtetijd
- Speciale relativiteit
- Algemene relativiteit
| Autoriteitcontrole: Nationale bibliotheken |
|
Vragen en antwoorden
V: Wat is de Minkowski-ruimtetijd?
A: De Minkowski-ruimtetijd is een vierdimensionale vorm gecreëerd door Hermann Minkowski. Het heeft drie dimensies van ruimte (x, y, z) en één dimensie van tijd.
V: Wat is de metrische handtekening van de Minkowski-ruimtetijd?
A: De metrische handtekening van de Minkowski-ruimtetijd is (-++).
V: Hoe beschrijft de Minkowski-ruimtetijd een plat oppervlak?
A: Zonder massa beschrijft de Minkowski-ruimtetijd een plat oppervlak.
V: Is de Minkowski ruimtetijd van toepassing op algemene relativiteit?
A: Nee, Minkowski ruimtetijd is alleen van toepassing in de speciale relativiteit. De algemene relativiteit gebruikt het begrip gekromde ruimtetijd om de effecten van zwaartekracht en versnelde beweging te beschrijven.
V: Hoeveel dimensies heeft de Minkowsi ruimtetijd?
A: Minkowsi Ruimtetijd heeft vier dimensies - drie dimensies van ruimte (x, y, z) en één dimensie van tijd.
V: Wie heeft het concept van de Minkowsi Ruimtetijd bedacht?
A: Hermann Minkowksi creëerde het concept van de Minkowski-ruimtetijd.
Zoek in de encyclopedie




