Oud Chinees toonsysteem: wiskundige stemming, fretten en pentatonische schalen

Ontdek het oude Chinese toonsysteem: wiskundige stemming, fretten en pentatonische schalen — hoe 144 unieke frequenties ontstaan en traditionele klanken gevormd worden.

Het oude Chinese muzieksysteem berust op een eenvoudige maar vernuftige toepassing van wiskunde: men bouwt toonhoogtes op uit hele verhoudingen, met name de verhouding 3:2 (de reine kwint). Het meest herkenbare resultaat hiervan is het systeem met twaalf tonen per octaaf, vaak aangeduid als de shi'er lü (twaalf lǜ). Een concreet voorbeeld maakt het principe het duidelijkst.

Een praktisch voorbeeld: fretten en lengteverhoudingen

Stel dat je een snaarinstrument wilt maken waarop je alle tonen van het oude Chinese systeem kunt produceren. Volgens het voorbeeld maak je een houten kist met 105 cm lengte en plaatst je de snaarbruggen zo dat de snaarlengte tussen de bruggen 99 cm is. Vervolgens markeer je fretten op specifieke posities langs die 99 cm door telkens met de factoren 2/3 of 4/3 te vermenigvuldigen.

Let op de relatie tussen snaarlengte en toonhoogte: de frequentie van een snaar is omgekeerd evenredig met de lengte. Als je de snaarlengte met 2/3 vermenigvuldigt (korter maakt), wordt de frequentie 3/2 keer zo hoog — dat is precies een reine kwint. Omgekeerd komt een factor 4/3 overeen met een reine kwart (of met een kwint in de andere richting), en ook met octaafverschuivingen moet je rekening houden. We passen daarom soms een factor 2 toe (verdubbelen of halveren) om de berekende positie binnen de speelbare snaarlengte te houden (octaafreduktie of -verhoging).

Het beschreven stappenplan (zoals in het oorspronkelijke voorbeeld) gaat als volgt:

• Begin met de snaarlengte 99 cm.
• Vermenigvuldig 99 cm met 2/3 → 66 cm: plaats daar een fret (dit geeft een toon een reine kwint boven de open snaar).
• Vermenigvuldig 66 cm met 4/3 → 88 cm: plaats daar een fret.
• Vermenigvuldig 88 cm met 2/3 → ≈58,667 cm: plaats daar een fret.
• Vermenigvuldig 58,667 cm met 4/3 → ≈78,222 cm: plaats daar een fret.
• Vermenigvuldig 78,222 cm met 2/3 → ≈52,148 cm: plaats daar een fret.
• Vermenigvuldig ≈52,148 cm met 4/3 → ≈69,531 cm: plaats daar een fret.
• Vermenigvuldig ≈69,531 cm met 2/3 → ≈46,354 cm. Omdat dit te kort is om praktisch op de kast te markeren (en om het binnen dezelfde octaafzone te houden), verdubbel je die lengte naar ≈92,708 cm en markeer je daar een fret.
• Ga zo verder (vermenigvuldig afwisselend met 4/3 en 2/3 en breng de uitkomsten zonodig in de speelbare lengte door octaafverplaatsing) tot je elf fretten hebt neergelegd.

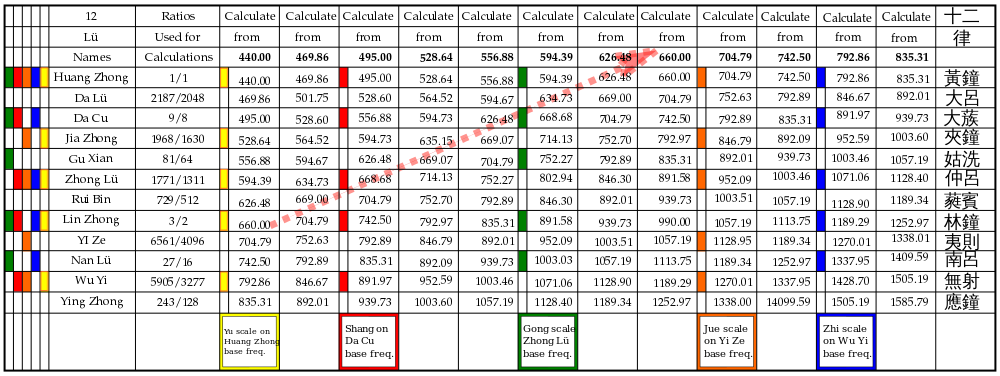
Door de frequenties (of, in de praktische benadering, de afstanden langs de snaar) van de open snaar en van de fretten te tellen, ontstaan er per snaar twaalf verschillende tonen binnen het octaaf. In het voorbeeld hierboven kun je vervolgens een reeks snaren stemmen: stem de onderste snaar op een gekozen basisfrequentie, de volgende snaar op de toon die de eerste fret van de onderste snaar produceert, de derde snaar op de toon die de tweede fret van de onderste snaar geeft, enzovoort — zo heb je uiteindelijk twaalf afzonderlijke snaren met elk een kolom van tonen. Als je alle fretten en open posities plukt krijg je zo 144 frequenties in totaal (waarbij veel tonen octaafgelijken of echte duplicaten kunnen zijn).

Wiskundige basis: de kwintencyclus en het Pythagoreïsche principe

De kern van dit systeem is de herhaalde toepassing van de verhouding 3:2 (de reine kwint). Als je een kwint telkens opnieuw opstapelt en de resulterende tonen terugbrengt naar hetzelfde octaaf (door delen of vermenigvuldigen met 2), ontstaat een cyclus van twaalf verschillende toonplaatsen binnen het octaaf. Dit is hetzelfde principe als in de Pythagoreïsche stemming of de traditionele Chinese shi'er lü. Belangrijk is dat deze tonen niet gelijk verdeeld zijn zoals in de moderne gelijkzwevende stemming; de intervallen verschillen iets van de gelijke-tolentoonsverdeling (equal temperament).

Door twaalf maal een kwint op te stapelen krijg je niet precies zeven octaven (er ontstaat een klein verschil dat bekendstaat als de Pythagorische komma). Daardoor kon men in het oude systeem prima zuivere kwinten krijgen, maar ontstaan er problemen wanneer je zeer veel modulaties of alle toonsoorten even zuiver wilt gebruiken — reden waarom veel moderne instrumenten naar gelijkzweving zijn overgegaan.

Pentatonische en andere toonladders

Uit elke verzameling van twaalf frequenties op één snaar kun je vele subsetten kiezen. Traditioneel heeft Chinese muziek een sterke voorkeur voor pentatonische toonladders: toonladders van vijf tonen. Vanuit de twaalfgrondtoonverdeling kies je vijf tonen die samen een aangename, karakteristieke pentatonische reeks vormen. In de Chinese traditie zijn vijf basismodaliteiten bekend, vaak genoemd met de karakters Gong (宮), Shang (商), Jiao (角), Zhi (徵) en Yu (羽). Elke mode komt overeen met een andere keuze van vijf tonen binnen de twaalf.

Een praktische regel bij het kiezen van pentatonische subsetten is dat de gekozen tonen niet te dicht bij elkaar mogen liggen en dat je meestal niet meer dan twee stappen van elkaar overslaat binnen de cyclische ordening van de twaalf tonen — op die manier voorkom je kleine secundes en krijg je de ruime, open karakteristiek die pentatonische muziek vaak heeft.

De oorspronkelijke tekst illustreerde ook grafisch hoe een basisfrequentie (bijvoorbeeld 440 hertz) via meerdere verhoudingen tot een kolom van twaalf frequenties leidt. Vanuit elke van die twaalf frequenties kun je weer een nieuwe kolom opbouwen; uit elke kolom kun je vervolgens pentatonische combinaties kiezen (zie ook de link over de pentatonische toonladder).

Verschil met moderne westerse stemming

In westerse muziekonderwijs is de bekende zeven-toonsreeks “do, re, mi, fa, sol, la, ti” de basis van de grote (majore) en kleine (minore) toonladders. Westerse muziekinstrumenten gebruiken tegenwoordig meestal de gelijkzwevende stemming, waarin de octaaf in twaalf gelijke halve tonen (factor 2^(1/12) per stap) is verdeeld. Het oude Chinese systeem daarentegen bouwt zuivere kwinten en kwartes met eenvoudige rationale verhoudingen, wat resulteert in andere intervalgroottes en een ander klankkarakter dan de gelijkzwevende stemming.

Historische en muzikale context

De methode met kwinten en het systeem van twaalf tonen heeft een lange geschiedenis in China (en heeft parallellen in de Griekse/Pythagoreïsche traditie). Instrumenten als de guqin, guzheng en andere traditionele snaarinstrumenten werden gestemd en bespeeld binnen deze verhoudingen, en de pentatonische modes zijn diep verankerd in de Chinese melodische praktijk. In de moderne tijd wordt in veel contexten echter ook de gelijkzwevende stemming gebruikt, vooral als westerse en Chinese instrumenten samen spelen.

Samenvattend: het oude Chinese toonsysteem gebruikt eenvoudige rationale verhoudingen (vooral 3:2) en octaafbrenging om een cyclus van twaalf niet-gelijkverdeelde tonen te verkrijgen. Uit die twaalf tonen worden vooral pentatonische toonladders gekozen, die het karakteristieke geluid van veel traditionele Chinese muziek bepalen.

Vragen en antwoorden

V: Waarop is het oude Chinese muzieksysteem gebaseerd?

V: Hoe maak je een muziekinstrument dat elk lied in het oude Chinese systeem kan spelen?

V: Wat is een voorbeeld van een heptatonische toonladder?

V: Hoeveel verschillende toonladders gebruikt de traditionele Chinese muziek?

V: Worden in dit artikel pentatonische toonladders besproken?

V: Welke frequentie is als voorbeeld gekozen?

V: Hoeveel frequenties worden geproduceerd wanneer alle twaalf snaren getokkeld worden op zowel gefrette als niet-gefrette posities?

Zoek op letter