Correlatie
In de statistiek en de waarschijnlijkheidsrekening betekent correlatie hoe nauw twee reeksen van gegevens met elkaar verbonden zijn.
Correlatie betekent niet altijd dat het een het ander veroorzaakt. Het is heel goed mogelijk dat er een derde factor in het spel is.
Correlatie heeft gewoonlijk één van twee richtingen. Deze zijn positief of negatief. Als de correlatie positief is, gaan de twee reeksen samen omhoog. Is ze negatief, dan gaat de ene omhoog terwijl de andere omlaag gaat.
Er worden veel verschillende metingen van correlatie gebruikt voor verschillende situaties. In een spreidingsgrafiek bijvoorbeeld, tekent men een best passende lijn om de richting van de correlatie aan te geven.
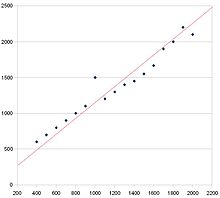
Deze spreidingsgrafiek heeft een positieve correlatie. Dat is te zien aan de stijgende en rechtse trend. De rode lijn is de best passende lijn.
Correlatie verklaren
Sterk en zwak zijn woorden die worden gebruikt om correlatie te beschrijven. Als er een sterke correlatie is, dan liggen de punten dicht bij elkaar. Als er een zwakke correlatie is, liggen de punten ver uit elkaar. Er zijn manieren om getallen te laten aangeven hoe sterk de correlatie is. Deze metingen worden correlatiecoëfficiënten genoemd. De bekendste is de Pearson product-moment correlatiecoëfficiënt. Je stopt gegevens in een formule en die geeft je een getal. Als het getal 1 of -1 is, dan is er een sterke correlatie. Als het antwoord 0 is, dan is er geen correlatie. Een ander soort correlatiecoëfficiënt is de rangcorrelatiecoëfficiënt van Spearman.
Correlatie vs oorzakelijk verband
Correlatie betekent niet altijd dat het ene het andere veroorzaakt (oorzakelijk verband), omdat iets anders beide veroorzaakt kan hebben. Bijvoorbeeld, op warme dagen kopen mensen ijs, en mensen gaan ook naar het strand waar sommigen worden opgegeten door haaien. Er bestaat een correlatie tussen de ijsverkoop en de haaienaanvallen (in dit geval stijgen ze allebei als de temperatuur stijgt). Maar het feit dat de ijsverkoop stijgt, betekent niet dat de ijsverkoop de oorzaak is van (causaal verband) meer haaienaanvallen of vice versa.
Omdat correlatie geen oorzakelijk verband impliceert zullen wetenschappers, economen, enz. hun theorieën testen door geïsoleerde omgevingen te creëren waarin slechts één factor wordt veranderd (voor zover dit mogelijk is). Politici, verkopers, nieuwszenders en anderen suggereren echter vaak dat een bepaalde correlatie een oorzakelijk verband impliceert. Dit kan het gevolg zijn van onwetendheid of van een wens om te overtuigen. Zo kan een nieuwsbericht de aandacht trekken door te zeggen dat mensen die een bepaald product vaker consumeren een bepaald gezondheidsprobleem hebben, waarbij een oorzakelijk verband wordt gesuggereerd dat in feite aan iets anders te wijten zou kunnen zijn.
Verwante pagina's
- Cohen, J., Cohen P., West, S.G., & Aiken, L.S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (Toegepaste meervoudige regressie/correlatieanalyse voor de gedragswetenschappen). (3rd ed.) Hillsdale, NJ: Lawrence Erlbaum Associates.
Vragen en antwoorden
V: Wat is correlatie?
A: Correlatie is een manier om aan te geven hoe nauw twee reeksen gegevens met elkaar verbonden zijn.
V: Betekent correlatie dat de ene reeks gegevens de andere veroorzaakt?
A: Nee, correlatie betekent niet altijd dat de ene set gegevens de andere veroorzaakt. In feite is er vaak een derde factor in het spel.
V: Wat zijn de twee richtingen van correlatie?
A: De twee richtingen van correlatie zijn positief en negatief.
V: Wat betekent een positieve correlatie?
A: Een positieve correlatie betekent dat de twee reeksen gegevens samen stijgen.
V: Wat betekent een negatieve correlatie?
A: Een negatieve correlatie betekent dat de ene reeks gegevens stijgt terwijl de andere daalt.
V: Zijn er verschillende metingen van correlatie?
A: Ja, er worden veel verschillende metingen van correlatie gebruikt voor verschillende situaties.
V: Hoe geven mensen vaak de richting van correlatie aan op een scatter grafiek?
A: Mensen tekenen vaak een best passende lijn om de richting van de correlatie op een spreidingsgrafiek weer te geven.
Zoek in de encyclopedie