Verzameling (wiskunde) | een idee uit de wiskunde

Een verzameling is een idee uit de wiskunde. Een verzameling heeft leden (ook wel elementen genoemd). Een verzameling wordt gedefinieerd door haar leden, dus twee verzamelingen met dezelfde leden zijn hetzelfde (bijv. als de verzameling X {\displaystyle {\mathit {X}}} ${\mathit {X}}$ en de verzameling Y {\mathit {Y}}} ${\mathit {Y}}$ dezelfde leden hebben, dan is X = Y {\mathit {X}}={\mathit {Y}}} ${\mathit {X}}={\mathit {Y}}$ ).

Een verzameling kan niet meer dan één keer hetzelfde lid hebben. Het lidmaatschap is het enige dat telt. Zo is er geen volgorde of ander verschil tussen de leden. Alles kan lid zijn van een verzameling, ook verzamelingen zelf (hoewel als een verzameling lid is van zichzelf, er paradoxen kunnen ontstaan zoals de paradox van Russell).

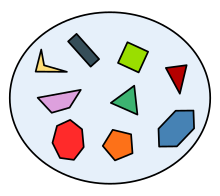
Voorbeeld van een verzameling veelhoeken

Georg Cantor, in 1894. Cantor was de eerste wiskundige die sprak over verzamelingen

Cantors oorspronkelijke definitie van een verzameling

Wat te doen met sets

Stel u voor dat de set een tas is.

Element van

Verschillende dingen kunnen in een zak worden gestopt. Later zou een goede vraag zijn of een bepaald ding in de zak zit. Wiskundigen noemen dit element van. Iets is een element van een verzameling, als dat ding in de betreffende zak zit. Het symbool hiervoor is ∈ $\in$ :

a ∈ A {{emathit {A}}}. $a\in {\mathit {A}}$ ,

wat betekent dat een {\displaystyle a} in de zak A {\displaystyle {\mathit {A}}} ${\mathit {A}}$ zit of een {\displaystyle a} een element is van A {\mathit {A}} ${\mathit {A}}$ .

In tegenstelling tot een zak kan een verzameling maximaal één voorwerp van een bepaald type bevatten. Voor een verzameling vruchten maakt het dus niet uit of er één sinaasappel is, of dat er 10 sinaasappels zijn.

Lege set

Net als een zak kan een verzameling ook leeg zijn. De lege verzameling is als een lege zak: er zit niets in. De "lege verzameling" wordt ook wel de nietige verzameling genoemd en wordt weergegeven door het symbool ∅ {{{}playstyle} $\varnothing$ .

Universum

Als wij bijvoorbeeld enkele reeksen Amerikaanse auto's beschouwen, bijvoorbeeld een reeks van alle Fords en een reeks van alle Dodges, kan het zijn dat wij ook de hele reeks Amerikaanse auto's willen beschouwen. In dat geval wordt de verzameling van alle Amerikaanse auto's een universum genoemd.

Met andere woorden, een universum is een verzameling van alle elementen die men in een bepaald probleem wil beschouwen. Het universum wordt gewoonlijk U genoemd: $U$ .

Sets vergelijken

Twee sets kunnen worden vergeleken. Dit is alsof u in twee verschillende zakken kijkt. Als ze dezelfde dingen bevatten, zijn ze gelijk. Het maakt niet uit in welke volgorde deze dingen staan.

Bijvoorbeeld, als A = { S t a n f o r d , S t a n l e y} { ${\mathit {A}}=\{Stanford,Stanley\}$ en B = {Stanford, Stanley, Stanley}} en B = { S t a n l e y , S t a n f o r d }. {Stanley,Stanford}}. ${\mathit {B}}=\{Stanley,Stanford\}$ zijn de verzamelingen hetzelfde.

Kardinaliteit van een verzameling

Wanneer wiskundigen over een verzameling spreken, willen zij soms weten hoe groot een verzameling is (of wat de kardinaliteit van de verzameling is). Zij doen dit door te tellen hoeveel elementen de verzameling bevat (hoeveel items er in de zak zitten). Voor eindige verzamelingen is de kardinaliteit een eenvoudig getal. De lege verzameling heeft een kardinaliteit van 0. De verzameling { a p p l e , o r a n g e } { $\{apple,orange\}$ heeft een kardinaliteit van 2.

Twee verzamelingen hebben dezelfde kardinaliteit als we hun elementen kunnen koppelen - als we twee elementen kunnen samenvoegen, één uit elke verzameling. De verzameling { a p p l e , o r a n g e } { $\{apple,orange\}$ en de verzameling {s u n , m o o n }. { $\{sun,moon\}$ hebben dezelfde kardinaliteit. We kunnen bijvoorbeeld appel koppelen aan zon, en sinaasappel aan maan. De volgorde maakt niet uit. Het is mogelijk om alle elementen te koppelen, en geen enkel element wordt weggelaten. Maar de verzameling { d o g , c a t , b i r d } { $\{dog,cat,bird\}$ en de set {5 , 6 } {kat,vogel}. { $\{5,6\}$ hebben een verschillende kardinaliteit. Als we ze proberen te koppelen, laten we altijd één dier weg.

Oneindige kardinaliteit

Soms is kardinaliteit geen getal. Soms heeft een verzameling oneindige kardinaliteit. De verzameling van alle gehele getallen is een verzameling met oneindige kardinaliteit. Sommige verzamelingen met oneindige kardinaliteit zijn groter (hebben een grotere kardinaliteit) dan andere. Er zijn bijvoorbeeld meer reële getallen dan natuurlijke getallen, wat betekent dat we de verzameling gehele getallen en de verzameling reële getallen niet kunnen koppelen, zelfs als we eeuwig zouden werken.

Telbaarheid

Als u de elementen van een verzameling kunt tellen, wordt deze een telbare verzameling genoemd. Tot de telbare verzamelingen behoren alle verzamelingen met een eindig aantal leden. Tot de telbare verzamelingen behoren ook enkele oneindige verzamelingen, zoals de natuurlijke getallen. U kunt de natuurlijke getallen tellen met 1 , 2 , 3... { ${1,2,3...}$ . De natuurlijke getallen hebben de bijnaam "de telgetallen", omdat we ze gewoonlijk gebruiken om dingen mee te tellen.

Een niet-telbare verzameling is een oneindige verzameling die onmogelijk te tellen is. Als we proberen de elementen te tellen, zullen we er altijd een paar overslaan. Het maakt niet uit welke stap we nemen. De verzameling reële getallen is een niet-telbare verzameling. Er zijn vele andere ontelbare verzamelingen, zelfs zo'n klein interval als [ 0 , 1 ] {\displaystyle [0,1]} $[0,1]$ .[3]

Subsets

Als u kijkt naar de verzameling A = {a , b } { $A=\{a,b\}$ en de verzameling B = {a , b , c , d } }. {displaystyle B={a,b,c,d}}. $B=\{a,b,c,d\}$ ziet u dat alle elementen van de eerste verzameling ook in de tweede verzameling voorkomen.
We zeggen: { a , b } { $\{a,b\}$ is een deelverzameling van { a , b , c , d }. {{a,b,c,d}}. $\{a,b,c,d\}$
Als formule ziet het er als volgt uit:
{ a , b } ⊆ { a , b , c , d } {{a,b}}{a,b,c,d}}. $\{a,b\}\subseteq \{a,b,c,d\}$

Wanneer alle elementen van de verzameling A {\displaystyle A} $A$ ook elementen zijn van de verzameling B {\displaystyle B} $B$ , noemen we A {\displaystyle A} $A$ een deelverzameling van B {\displaystyle B} $B$ :
A ⊆ B {\displaystyle A {\subseteq B} $A\subseteq B$ .
Meestal wordt gelezen " A {displaystyle A} $A$ is vervat in B {displaystyle B} $B$ ."

Voorbeeld: Elke Chevrolet is een Amerikaanse auto. Dus de verzameling van alle Chevrolets is vervat in de verzameling van alle Amerikaanse auto's.

Ingestelde operaties

Er zijn verschillende manieren om sets te combineren.

Kruispunten

De doorsnede A ∩ B {{displaystyle A} $A\cap B$ van twee verzamelingen A {displaystyle A} $A$ en B {displaystyle B} $B$ is een verzameling die alle elementen bevat die tegelijkertijd in de verzameling A {displaystyle A} $A$ en in de verzameling B {displaystyle B} $B$ zitten.

Voorbeeld: Wanneer A {{displaystyle A} $A$ de verzameling is van alle goedkope auto's, en B {{displaystyle B} $B$ de verzameling is van alle Amerikaanse auto's, dan is A ∩ B {{displaystyle A} $A\cap B$ de verzameling van alle goedkope Amerikaanse auto's.

Vakbonden

De unie A ∪ B {\displaystyle B} $A\cup B$ van twee verzamelingen A {\displaystyle A} $A$ en B {\displaystyle B} $B$ is een verzameling die alle elementen bevat die in de verzameling A {\displaystyle A} $A$ of in de verzameling B {\displaystyle B} $B$ zitten. Deze "of" is de inclusieve scheiding, dus de unie bevat ook de elementen uit de verzameling A {displaystyle A} $A$ en uit de verzameling B {displaystyle B} $B$ . Dit betekent overigens, dat de intersectie een deelverzameling is van de unie: ( A ∩ B ) ⊆ ( A ∪ $(A\cap B)\subseteq (A\cup B)$ .

Voorbeeld: Wanneer A {{displaystyle A} $A$ de verzameling is van alle goedkope auto's, en B {{displaystyle B} $B$ de verzameling is van alle Amerikaanse auto's, dan is A ∪ B {{displaystyle A} $A\cup B$ de verzameling van alle auto's, zonder alle dure auto's die niet uit Amerika komen.

Aanvullingen

Complement kan twee verschillende dingen betekenen:

Het complement van A {displaystyle A} $A$ is het universum U {displaystyle U} $U$ zonder alle elementen van A {displaystyle A} $A$ :

A C = U ∖ A {{\displaystyle A}=Usetminus A}. $A^{\rm {C}}=U\setminus A$
Het universum U {\displaystyle U} $U$ is de verzameling van alle dingen waarover je spreekt.
Voorbeeld: Wanneer U {\displaystyle U} $U$ de verzameling is van alle auto's, en A {\displaystyle A} $A$ de verzameling is van alle goedkope auto's,
dan is A {\displaystyle A} $A$ ^C de verzameling van alle dure auto's.

De verzameling verschil van A {displaystyle A} $A$ en B {displaystyle B} $B$ is de verzameling B {displaystyle B} $B$ zonder alle elementen van A {displaystyle A} $A$ :

B ∖ A {een min A}. $B\setminus A$
Dit wordt ook wel het relatieve complement van A {displaystyle A} $A$ in B {displaystyle B} $B$ genoemd.
Voorbeeld: Wanneer A {\displaystyle A} $A$ de verzameling is van alle goedkope auto's, en B {\displaystyle B} $B$ de verzameling is van alle Amerikaanse auto's, dan is B ∖ A {\displaystyle B} $B\setminus A$ de verzameling van alle dure Amerikaanse auto's.

Als u de sets in de set verschil omwisselt, is het resultaat anders:
In het voorbeeld met de auto's is het verschil A ∖ B {het verschil met B} $A\setminus B$ de set van alle goedkope auto's, die niet in Amerika zijn gemaakt.

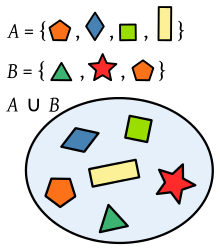
Unie van twee reeksen veelhoeken

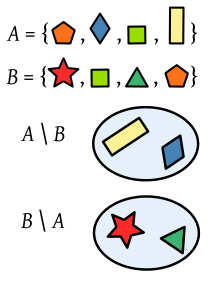
Verschillen van twee reeksen veelhoeken

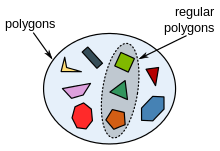
Een deelverzameling van regelmatige veelhoeken

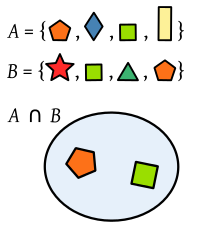
Snijpunt van twee reeksen veelhoeken

Notatie

De meeste wiskundigen gebruiken hoofdletters om over verzamelingen te schrijven (zoals A {{displaystyle A} $A$ , B {{displaystyle B} $B$ , C {{displaystyle C} $C$ ). De dingen die gezien worden als elementen van verzamelingen worden meestal geschreven met Romeinse kleine letters.

Een manier om een verzameling weer te geven is door een lijst van de leden, gescheiden door komma's, tussen accolades. Bijvoorbeeld,

X = { 1 , 2 , 3 } { $X=\{1,2,3\}$ is een verzameling waarvan de leden 1, 2 en 3 zijn.

Een andere manier, genaamd de verzameling-notatie, is door een verklaring van wat waar is voor de leden van de verzameling, zoals deze:

{x | x is een natuurlijk getal & x < 4}.

In gesproken Engels luidt dit: "de verzameling van alle x zodanig dat x een natuurlijk getal is en x kleiner is dan vier". Het symbool [ipe "|" betekent "zodanig dat" of "zodat".

De lege verzameling wordt op een speciale manier geschreven: ∅ {{{empty}}. $\emptyset$ , ∅ {\displaystyle \varnothing } $\varnothing$ of {\displaystyle \{}}. $\{\}$ .

Wanneer object a lid is van de verzameling A {A} $A$ wordt het geschreven als:

$a$ $\in$ $A$ .

In gesproken Engels luidt dit: "a is een lid van A {\displaystyle A} $A$ ".

Venn-diagrammen

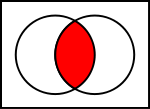
Om bewerkingen op verzamelingen te illustreren gebruiken wiskundigen Venn-diagrammen. Venn-diagrammen gebruiken cirkels om individuele verzamelingen weer te geven. Het universum wordt weergegeven met een rechthoek. Resultaten van bewerkingen worden weergegeven als gekleurde gebieden. In de illustratie van de snijbewerking toont de linkercirkel de verzameling A {displaystyle A} $A$ en de rechtercirkel de verzameling B {displaystyle B} $B$ .

Snijpunt A ∩ B $A\cap B$

Speciale sets

Sommige verzamelingen zijn zeer belangrijk voor de wiskunde. Ze worden heel vaak gebruikt. Een daarvan is de lege verzameling. Veel van deze speciale verzamelingen worden geschreven in een vetgedrukt schoolbordlettertype, zoals:

P {\displaystyle \mathbb {P} } $\mathbb {P}$ , zijnde de verzameling van alle priemgetallen.
N {\displaystyle \mathbb {N} } $\mathbb {N}$ de verzameling van alle natuurlijke getallen. Dat wil zeggen, N {\mathbb {N} } $\mathbb {N}$ = {1, 2, 3, ...}, of soms N {displaystyle \mathbb {N}} } $\mathbb {N}$ = {0, 1, 2, 3, ...}.
Z {\displaystyle \mathbb {Z} } $\mathbb {Z}$ , de verzameling van alle gehele getallen (positief, negatief of nul). Dus Z {\mathbb {Z} } $\mathbb {Z}$ = {..., -2, -1, 0, 1, 2, ...}.
Q {{"displaystyle" \mathbb {Q}} } $\mathbb {Q}$ , de verzameling van alle rationale getallen (dat wil zeggen de verzameling van alle eigenlijke en oneigenlijke breuken). Dus Q = { a b | a , b ∈ Z , b ≠ 0 }. {Q = {begin{matrix}{frac {a}{b}}}eind{matrix}}|a,b in \mathbb {Z}, b ≠ 0}. b, bneq 0, rechtdoor}}. $\mathbb {Q} =\left\{{\begin{matrix}{\frac {a}{b}}\end{matrix}}|a,b\in \mathbb {Z} ,b\neq 0\right\}$ Dat wil zeggen alle fracties a b ${\begin{matrix}{\frac {a}{b}}\end{matrix}}$ waarbij a en b behoren tot de verzameling van alle gehele getallen en b niet gelijk is aan 0. Bijvoorbeeld, 1 4 ∈ Q {displaystyle {begin{matrix}{frac {1}{4}}}{end{matrix}}} in \mathbb {Q}}. } ${\begin{matrix}{\frac {1}{4}}\end{matrix}}\in \mathbb {Q}$ en 11 6 ∈ Q {\begin{matrix}{frac {11}{6}}}}end{matrix}} in \mathbb {Q}}. } ${\begin{matrix}{\frac {11}{6}}\end{matrix}}\in \mathbb {Q}$ . Alle gehele getallen zitten in deze verzameling omdat elk geheel getal a kan worden uitgedrukt als de breuk a 1 {displaystyle {begin{matrix}{frac {a}{1}}}} ${\begin{matrix}{\frac {a}{1}}\end{matrix}}$ .
R {\mathbb {R} }. $\mathbb {R}$ de verzameling van alle reële getallen. Deze verzameling omvat alle rationale getallen, samen met alle irrationele getallen (dat wil zeggen getallen die niet als breuken kunnen worden herschreven, zoals π , {\displaystyle \pi,} $\pi ,$ e , {\displaystyle e,} $e,$ en √2).
C {displaystyle \mathbb {C} } $\mathbb {C}$ , de verzameling van alle complexe getallen.

Elk van deze getallenreeksen heeft een oneindig aantal elementen, en P ⊂ N ⊂ Z ⊂ Q ⊂ R ⊂ $\mathbb {P} \subset \mathbb {N} \subset \mathbb {Z} \subset \mathbb {Q} \subset \mathbb {R} \subset \mathbb {C}$ .

Paradoxen over verzamelingen

De wiskundige Bertrand Russell vond dat er problemen zijn met de informele definitie van verzamelingen. Hij formuleerde dit in een paradox die Russells paradox wordt genoemd. Een gemakkelijker te begrijpen versie, die dichter bij het echte leven staat, heet de Barber-paradox.

De kappersparadox

Er is ergens een kleine stad. In dat stadje is er een barbier. Alle mannen in het stadje houden niet van baarden, dus ofwel scheren ze zichzelf, ofwel gaan ze naar de barbier om zich door de barbier te laten scheren.

We kunnen dus een uitspraak doen over de barbier zelf: De barbier scheert alle mannen die zichzelf niet scheren. Hij scheert alleen die mannen (aangezien de anderen zichzelf scheren en geen barbier nodig hebben om hen te scheren).

Dit roept natuurlijk de vraag op: Wat doet de kapper elke ochtend om er gladgeschoren uit te zien? Dit is de paradox.

Als de barbier zichzelf scheert, kan hij geen barbier zijn, want een barbier scheert zichzelf niet. Als hij zich niet scheert, valt hij in de categorie van degenen die zich niet scheren, en kan hij dus geen barbier zijn.

Gerelateerde pagina's

Cantorreeks
Groepentheorie
Open set
Relatie
Set theorie

Vragen en antwoorden

V: Wat is een set?

A: Een verzameling is een idee uit de wiskunde. Het bestaat uit leden (ook wel elementen genoemd) die gedefinieerd worden door hun leden, dus twee verzamelingen met dezelfde leden zijn hetzelfde.

V: Kan een verzameling meer dan eens hetzelfde lid hebben?

A: Nee, een verzameling kan niet meer dan één keer hetzelfde lid hebben.

V: Is de volgorde van belang in een verzameling?

A: Nee, de volgorde is niet van belang in een verzameling. Alles kan lid zijn van een verzameling, ook de verzamelingen zelf.

V: Wat gebeurt er als een verzameling lid is van zichzelf?

A: Als een verzameling lid is van zichzelf, kunnen paradoxen zoals de paradox van Russell zich voordoen.

V: Is lidmaatschap het enige dat telt voor verzamelingen?

A: Ja, lidmaatschap is het enige dat telt voor verzamelingen.

V: Hoe weet u of twee verzamelingen gelijk zijn?

Antwoord: Twee verzamelingen zijn gelijk als ze dezelfde leden hebben.