Statistiek | tak van toegepaste wiskunde die zich bezighoudt met het verzamelen, organiseren, analyseren, lezen en presenteren van gegevens
Statistiek is een tak van de toegepaste wiskunde die zich bezighoudt met het verzamelen, ordenen, analyseren, aflezen en presenteren van gegevens. Beschrijvende statistieken maken samenvattingen van gegevens. Inferentiële statistieken maken voorspellingen. Statistiek helpt bij de studie van vele andere gebieden, zoals wetenschap, geneeskunde, economie, psychologie, politiek en marketing. Iemand die zich bezighoudt met statistiek wordt een statisticus genoemd. Het woord "statistiek" is niet alleen de naam van een studiegebied, maar kan ook cijfers betekenen die worden gebruikt om gegevens of relaties te beschrijven.
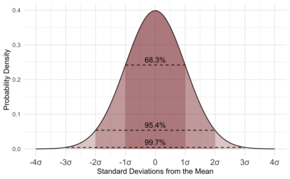
De normale verdeling in de statistiek
Geschiedenis
De eerste bekende statistieken zijn volkstellingsgegevens. De Babyloniërs hielden een volkstelling rond 3500 voor Christus, de Egyptenaren rond 2500 voor Christus, en de oude Chinezen rond 1000 voor Christus.
Vanaf de 16e eeuw ontwikkelden wiskundigen zoals Gerolamo Cardano de waarschijnlijkheidstheorie, waardoor statistiek een wetenschap werd. Sindsdien hebben mensen statistieken over vele dingen verzameld en bestudeerd. Bomen, zeesterren, sterren, rotsen, woorden, bijna alles wat geteld kan worden is onderwerp geweest van statistiek.
Gegevens verzamelen
Voordat we de wereld kunnen beschrijven met statistieken, moeten we gegevens verzamelen. De gegevens die wij in de statistiek verzamelen, worden metingen genoemd. Nadat we gegevens hebben verzameld, gebruiken we een of meer getallen om elke waarneming of meting te beschrijven. Stel bijvoorbeeld dat wij willen weten hoe populair een bepaald tv-programma is. We kunnen een groep mensen (een steekproef genoemd) kiezen uit de totale populatie kijkers. Vervolgens vragen wij elke kijker in de steekproef hoe vaak zij naar de show kijken. De steekproef zijn gegevens die men kan zien, en de populatie zijn gegevens die men niet kan zien (ervan uitgaande dat niet elke kijker in de populatie wordt gevraagd). Een ander voorbeeld: als we willen weten of een bepaald medicijn kan helpen de bloeddruk te verlagen, kunnen we het medicijn enige tijd aan mensen geven en hun bloeddruk voor en na meten.
Beschrijvende en inferentiële statistieken
Getallen die de gegevens beschrijven die men kan zien, worden beschrijvende statistieken genoemd. Getallen die voorspellingen doen over gegevens die men niet kan zien, worden inferentiële statistieken genoemd.
Bij beschrijvende statistiek worden getallen gebruikt om kenmerken van gegevens te beschrijven. De gemiddelde lengte van vrouwen in de Verenigde Staten is bijvoorbeeld een beschrijvende statistiek: het beschrijft een kenmerk (gemiddelde lengte) van een populatie (vrouwen in de Verenigde Staten).
Zodra de resultaten zijn samengevat en beschreven, kunnen ze worden gebruikt voor voorspellingen. Dit wordt inferentiële statistiek genoemd. Een voorbeeld: de grootte van een dier is afhankelijk van vele factoren. Sommige van deze factoren worden bepaald door het milieu, maar andere door overerving. Een bioloog zou daarom een model kunnen maken dat zegt dat er een grote kans is dat de nakomelingen klein van formaat zullen zijn - als de ouders klein van formaat waren. Met dit model kan de grootte waarschijnlijk beter worden voorspeld dan met een willekeurige gok. Testen of een bepaald geneesmiddel een bepaalde aandoening of ziekte kan genezen, gebeurt meestal door de resultaten van mensen die het geneesmiddel krijgen te vergelijken met mensen die een placebo krijgen.
Methoden
Meestal verzamelen wij statistische gegevens door middel van enquêtes of experimenten. Een enquête is bijvoorbeeld een opiniepeiling. Wij kiezen een klein aantal mensen en stellen hen vragen. Vervolgens gebruiken wij hun antwoorden als gegevens.
De keuze van de personen die worden genomen voor een enquête of gegevensverzameling is belangrijk, omdat dit rechtstreeks van invloed is op de statistieken. Als de statistieken klaar zijn, kan niet meer worden bepaald welke individuen worden genomen. Stel dat we de waterkwaliteit van een groot meer willen meten. Als we monsters nemen naast de afvoer, krijgen we andere resultaten dan wanneer de monsters worden genomen op een verafgelegen en moeilijk bereikbare plek van het meer.
Er zijn twee soorten problemen die vaak voorkomen bij het nemen van monsters:
- Als er veel steekproeven zijn, zullen de steekproeven waarschijnlijk heel dicht bij de werkelijke populatie liggen. Als er echter heel weinig steekproeven zijn, kunnen ze heel anders zijn dan in de echte populatie. Deze fout wordt een toevalsfout genoemd (zie ook Fouten en residuen in de statistiek).
- De personen voor de steekproeven moeten zorgvuldig worden gekozen. Meestal worden ze willekeurig gekozen. Als dit niet het geval is, kunnen de steekproeven sterk afwijken van wat ze werkelijk zijn in de totale populatie. Dit geldt zelfs als er een groot aantal steekproeven wordt genomen. Dit soort fout wordt bias genoemd.
Fouten
We kunnen toevallige fouten verminderen door een grotere steekproef te nemen, en we kunnen enige vertekening vermijden door willekeurig te kiezen. Soms is het echter moeilijk om grote aselecte steekproeven te nemen. En vertekening kan optreden als verschillende mensen niet gevraagd worden, of weigeren onze vragen te beantwoorden, of als ze weten dat ze een nepbehandeling krijgen. Deze problemen kunnen moeilijk te verhelpen zijn. Zie Standaardfout voor meer informatie.
Beschrijvende statistieken
Het midden van de gegevens vinden
Het midden van de gegevens wordt een gemiddelde genoemd. Het gemiddelde zegt iets over een typisch individu in de populatie. Er zijn drie soorten gemiddelden die vaak worden gebruikt: het gemiddelde, de mediaan en de modus.
De onderstaande voorbeelden maken gebruik van deze voorbeeldgegevens:
| Naam | A | B | C | D | E | F | G | H | I | J |
| Score | 23 | 26 | 49 | 49 | 57 | 64 | 66 | 78 | 82 | 92 |
Gemiddelde
De formule voor het gemiddelde is
Waarbij 

Dit betekent dat men het gemiddelde berekent door alle waarden op te tellen en vervolgens te delen door het aantal waarden. Voor het bovenstaande voorbeeld is het gemiddelde:
Het probleem met het gemiddelde is dat het niets zegt over hoe de waarden verdeeld zijn. Waarden die heel groot of heel klein zijn, veranderen het gemiddelde sterk. In de statistiek kunnen deze extreme waarden meetfouten zijn, maar soms bevat de populatie echt deze waarden. Bijvoorbeeld, als er 10 mensen in een kamer zijn die $10 per dag verdienen en 1 die $1.000.000 per dag verdient. Het gemiddelde van de gegevens is $90.918 per dag. Hoewel dit het gemiddelde is, is het gemiddelde in dit geval niet het bedrag dat een individuele persoon verdient, en dus niet erg nuttig voor sommige doeleinden.
Het hierboven beschreven gemiddelde is het "rekenkundig gemiddelde". Andere soorten zijn nuttig voor bepaalde doeleinden.
Mediaan
De mediaan is het middelste item van de gegevens. Voor een gegeven gegeven 

Als ander voorbeeld, zoals het inkomensvoorbeeld voor het gemiddelde, neem een kamer met 10 mensen met inkomens van $10, $20, $20, $40, $50, $60, $90, $90, $100, en $1.000.000. Hier is de mediaan $55, omdat $55 het gemiddelde is van de twee middelste getallen, $50 en $60. Als de extreme waarde van $1.000.000 wordt genegeerd, is het gemiddelde $53. In dit geval ligt de mediaan dicht bij de waarde die wordt verkregen als de extreme waarde wordt weggegooid. De mediaan lost het probleem van extreme waarden op, zoals beschreven in de definitie van het gemiddelde hierboven.
Modus
De modus is het meest voorkomende gegeven. De meest voorkomende letter in het Engels is bijvoorbeeld de letter "e". Wij zouden zeggen dat "e" de modus is van de verdeling van de letters.
Een ander voorbeeld: als er 10 mensen in een kamer zijn met inkomens van $10, $20, $20, $40, $50, $60, $90, $90, $100 en $1.000.000, dan is de modus $90, omdat $90 drie keer voorkomt en alle andere waarden minder dan drie keer.
Er kan meer dan één modus zijn. Als er bijvoorbeeld 10 mensen in een kamer zijn met inkomens van $10, $20, $20, $50, $60, $90, $90, $100, en $1.000.000, dan zijn de modi $20 en $90. Dit is bi-modaal, oftewel heeft twee modi. Bi-modaliteit komt veel voor, en geeft vaak aan dat de gegevens een combinatie zijn van twee verschillende groepen. Zo heeft de gemiddelde lengte van alle volwassenen in de VS een bi-modale verdeling. Dit komt doordat mannen en vrouwen een afzonderlijke gemiddelde lengte hebben van 1,763 m voor mannen en 1,622 m voor vrouwen. Deze pieken worden duidelijk wanneer beide groepen worden gecombineerd.
De modus is de enige vorm van gemiddelde die kan worden gebruikt voor gegevens die niet op volgorde kunnen worden gezet.
De spreiding van de gegevens vinden
Iets anders wat we kunnen zeggen over een reeks gegevens is de spreiding ervan. Een gebruikelijke manier om de spreiding van een gegevensreeks te beschrijven is de standaardafwijking. Als de standaardafwijking van een gegevensreeks klein is, dan liggen de meeste gegevens heel dicht bij het gemiddelde. Is de standaardafwijking echter groot, dan wijken veel gegevens sterk af van het gemiddelde.
De standaardafwijking van een steekproef verschilt doorgaans van de standaardafwijking van de oorspronkelijke populatie. Daarom schrijven we 

Als de gegevens het algemene patroon volgen dat de normale verdeling wordt genoemd, dan is het zeer nuttig om de standaardafwijking te kennen. Als de gegevens dit patroon volgen (we zouden zeggen dat de gegevens normaal verdeeld zijn), zullen ongeveer 68 van elke 100 gegevens minder dan de standaardafwijking van het gemiddelde afwijken. Niet alleen dat, maar ongeveer 95 van elke 100 metingen zullen minder dan twee keer de standaarddeviatie van het gemiddelde afwijken, en ongeveer 997 op de 1000 zullen minder dan drie standaarddeviaties dichter bij het gemiddelde liggen.
Andere beschrijvende statistieken
Wij kunnen statistieken ook gebruiken om vast te stellen dat een bepaald percentage, percentiel, aantal of fractie van mensen of dingen in een groep iets doen of in een bepaalde categorie passen.
Sociale wetenschappers gebruikten bijvoorbeeld statistieken om vast te stellen dat 49% van de mensen in de wereld mannen zijn.
Verwante software
Ter ondersteuning van statistici is veel statistische software ontwikkeld:
- MATLAB
- R
- SAS Instituut
- SPSS (gemaakt door IBM)
Vragen en antwoorden
V: Wat is statistiek?
A: Statistiek is een tak van de toegepaste wiskunde die zich bezighoudt met het verzamelen, organiseren, analyseren, lezen en presenteren van gegevens.
V: Wat zijn de twee soorten statistiek?
A: De twee soorten statistieken zijn beschrijvende en inferentiële statistieken. Beschrijvende statistieken maken samenvattingen van gegevens, terwijl inferentiële statistieken voorspellingen doen.
V: Hoe helpt statistiek op andere gebieden?
A: Statistiek helpt bij de studie van vele andere gebieden zoals wetenschap, geneeskunde, economie, psychologie, politiek en marketing.
V: Wie werkt er in de statistiek?
A: Iemand die werkzaam is op het gebied van de statistiek wordt een statisticus genoemd.
V: Wat betekent het woord "statistiek"?
A: Het woord "statistiek" is niet alleen de naam van een studiegebied, maar kan ook cijfers betekenen die worden gebruikt om gegevens of relaties te beschrijven.
V: Welke activiteiten ontplooien statistici?
A: Statistici houden zich bezig met activiteiten zoals het verzamelen, organiseren, analyseren, lezen en presenteren van gegevens.
Zoek in de encyclopedie

