Vierkleurenstelling | stelling uit de wiskunde
De stelling van de vier kleuren is een stelling uit de wiskunde. Het zegt dat in elk vlak oppervlak met gebieden erin (men denkt aan kaarten), de gebieden met niet meer dan vier kleuren kunnen worden gekleurd. Twee gebieden die een gemeenschappelijke grens hebben, mogen niet dezelfde kleur krijgen. Zij worden aangrenzend (naast elkaar) genoemd als zij een segment van de grens delen, niet alleen een punt.
Dit was de eerste stelling die werd bewezen door een computer, in een bewijs door uitputting. Bij een bewijs door uitputting wordt de conclusie vastgesteld door deze op te delen in gevallen, en elk geval apart te bewijzen. Er kunnen veel gevallen zijn. Zo was het eerste bewijs van het vierkleurentheorema een uitputtingsbewijs met 1.936 gevallen. Dit bewijs was controversieel omdat de meeste gevallen werden gecontroleerd door een computerprogramma, niet met de hand. Het kortst bekende bewijs van het vierkleurentheorema heeft vandaag de dag nog steeds meer dan 600 gevallen.
Hoewel het probleem eerst werd voorgesteld als een probleem om politieke landkaarten in te kleuren, zijn kaartenmakers er niet erg in geïnteresseerd. Volgens een artikel van de wiskundehistoricus Kenneth May (Wilson 2002, 2), "zijn kaarten die slechts vier kleuren gebruiken zeldzaam, en de kaarten die dat wel doen hebben er meestal maar drie nodig. Boeken over cartografie en de geschiedenis van het maken van kaarten maken geen melding van de vierkleuren-eigenschap."
Veel eenvoudigere kaarten kunnen worden ingekleurd met drie kleuren. De vierde kleur is nodig voor sommige kaarten, zoals een kaart waarin een gebied wordt omgeven door een oneven aantal andere, die elkaar in een cyclus raken. Een dergelijk voorbeeld wordt gegeven in de afbeelding. De stelling van vijf kleuren stelt dat vijf kleuren voldoende zijn om een kaart te kleuren. Het heeft een kort, elementair bewijs en werd eind 19e eeuw bewezen. (Heawood 1890) Het bewijzen dat vier kleuren voldoende zijn, bleek veel moeilijker. Sinds de eerste verklaring van het vierkleurentheorema in 1852 zijn er veel valse bewijzen en valse tegenvoorbeelden verschenen.

Voorbeeld van een kaart met vier kleuren

Drie kleuren zijn niet genoeg om deze kaart in te kleuren.
Exacte formulering van het probleem
Intuïtief kan de stelling van de vier kleuren worden geformuleerd als "gegeven een verdeling van een vlak in aaneengesloten gebieden, een kaart genoemd, kunnen de gebieden worden gekleurd met maximaal vier kleuren zodat geen twee aangrenzende gebieden dezelfde kleur hebben". Om het probleem correct te kunnen oplossen, moeten enkele aspecten worden verduidelijkt: Ten eerste moeten alle punten die tot drie of meer landen behoren, worden genegeerd. Ten tweede kunnen bizarre kaarten met regio's van eindige oppervlakte en oneindige omtrek meer dan vier kleuren vereisen.
Voor het doel van de stelling moet elk "land" een eenvoudig verbonden regio zijn, of aaneengesloten. In de echte wereld is dit niet waar: Alaska als deel van de Verenigde Staten, Nachchivan als deel van Azerbeidzjan, en Kaliningrad als deel van Rusland zijn niet aaneengesloten. Omdat het grondgebied van een bepaald land dezelfde kleur moet hebben, kunnen vier kleuren niet genoeg zijn. Neem bijvoorbeeld een vereenvoudigde kaart, zoals die hiernaast: Op deze kaart behoren de twee gebieden met het label A tot hetzelfde land, en moeten ze dezelfde kleur hebben. Deze kaart vereist dan vijf kleuren, aangezien de twee regio's van A samen grenzen aan vier andere regio's, die elk grenzen aan alle andere. Als A slechts drie regio's had, zouden zes of meer kleuren nodig zijn. Op deze manier is het mogelijk kaarten te maken die een willekeurig hoog aantal kleuren nodig hebben. Een soortgelijke constructie geldt ook als één kleur wordt gebruikt voor alle waterlichamen, zoals gebruikelijk is op echte kaarten.
Een eenvoudiger te formuleren versie van de stelling maakt gebruik van de grafiektheorie. De verzameling regio's van een kaart kan abstracter worden voorgesteld als een ongerichte grafiek met een vertex voor elke regio en een rand voor elk paar regio's die een grenssegment delen. Deze grafiek is vlak: hij kan zonder kruisingen in het vlak worden getekend door elk hoekpunt op een willekeurig gekozen plaats te zetten binnen de regio waarmee hij overeenkomt, en door de randen te tekenen als krommen die zonder kruisingen binnen elke regio leiden van de plaats van het hoekpunt naar elk gedeeld grenspunt van de regio. Omgekeerd kan elke vlakke grafiek op deze manier uit een kaart worden gevormd. In grafiektheoretische terminologie stelt de vierkleurentheorie dat de hoekpunten van elke vlakke grafiek kunnen worden gekleurd met ten hoogste vier kleuren, zodat geen twee aangrenzende hoekpunten dezelfde kleur hebben, of kortweg: "elke vlakke grafiek is vierkleurbaar" (Thomas 1998, blz. 849; Wilson 2002).

Voorbeeld van een kaart van Azerbeidzjan met niet-aaneengesloten gebieden

Deze kaart kan niet met vier kleuren worden ingekleurd
Geschiedenis
De eerste persoon die het probleem benoemde was Francis Guthrie, in 1852. Hij studeerde toen rechten in Engeland. Hij ontdekte dat hij minstens vier kleuren nodig had om een kaart van de graafschappen van Engeland in te kleuren. Augustus de Morgan besprak het probleem voor het eerst in een brief die hij in augustus 1852 aan Rowan Hamliton schreef. In de brief vraagt de Morgan of vier kleuren echt genoeg zijn om een kaart in te kleuren, zodat landen die naast elkaar liggen verschillende kleuren krijgen.
De Engelse wiskundige Arthur Cayley presenteerde het probleem in 1878 aan het wiskundig genootschap in Londen. Binnen een jaar vond Alfred Kempe wat leek op een bewijs van het probleem. Elf jaar later, in 1890, toonde Percy Heawood aan dat Alfreds bewijs fout was. Peter Guthrie Tait presenteerde in 1880 een andere poging tot een bewijs. Het duurde elf jaar om aan te tonen dat ook Tait's bewijs niet werkte. In 1891 kon Julius Petersen dit aantonen. Toen hij Cayley's bewijs falsificeerde, toonde Kempe ook een bewijs voor een probleem dat hij Vijfkleurtheorema noemde. De stelling zegt dat een dergelijke kaart met niet meer dan vijf kleuren kan worden ingekleurd. Er zijn twee beperkingen: Ten eerste is elk land aaneengesloten, er zijn geen exclaves. De tweede beperking is dat landen een gemeenschappelijke grens moeten hebben; als ze elkaar alleen in een punt raken, kunnen ze met dezelfde kleur worden gekleurd. Hoewel Kempe's bewijs fout was, gebruikte hij enkele ideeën die later een correct bewijs mogelijk zouden maken.
In de jaren 1960 en 1970 ontwikkelde Heinrich Heesch een eerste schets van een computerbewijs. Kenneth Appel en Wolfgang Haken verbeterden deze schets in 1976 (Robertson et al. 1996). Zij konden het aantal gevallen dat moest worden getest terugbrengen tot 1936; een latere versie ging uit van het testen van slechts 1476 gevallen. Elk geval moest door een computer worden getest (Appel & Haken 1977) harv fout: meerdere doelen (2×): CITEREFAppelHaken1977 (help).
In 1996 verbeterden Neil Robertson, Daniel Sanders, Paul Seymour en Robin Thomas de methode en brachten zij het aantal te testen gevallen terug tot 663. Opnieuw moest elk geval per computer worden getest.
In 2005 ontwikkelden Georges Gonthier en Benjamin Werner een formeel bewijs. Dit was een verbetering, omdat het voor het eerst mogelijk was software voor het bewijzen van stellingen te gebruiken. De gebruikte software heet Coq.
Het vierkleurentheorema is het eerste grote wiskundige probleem dat werd bewezen met behulp van een computer. Omdat het bewijs niet door een mens kan worden gedaan, erkenden sommige wiskundigen het niet als correct. Om het bewijs te verifiëren is het noodzakelijk te vertrouwen op correct werkende software en hardware. Omdat het bewijs door de computer is gedaan, is het ook niet erg elegant.
Pogingen die fout bleken te zijn
Het vierkleurentheorema is berucht omdat het in zijn lange geschiedenis een groot aantal valse bewijzen en weerleggingen heeft opgeleverd. Aanvankelijk weigerde The New York Times te berichten over het Appel-Haken bewijs. De krant deed dit uit beleidsoverwegingen; zij vreesde dat het bewijs vals zou blijken te zijn, zoals de bewijzen daarvoor (Wilson 2002, p. 209). Sommige bewijzen duurden lang voordat ze konden worden vervalst: Voor Kempe's en Tait's bewijzen duurde het meer dan tien jaar om ze te vervalsen.
De eenvoudigste tegenvoorbeelden proberen meestal één gebied te maken dat alle andere raakt. Dit dwingt de overige regio's om met slechts drie kleuren te worden gekleurd. Omdat de stelling van vier kleuren waar is, is dit altijd mogelijk; maar omdat de persoon die de kaart tekent gericht is op die ene grote regio, merkt hij niet op dat de overige regio's in feite met drie kleuren kunnen worden gekleurd.
Deze truc kan worden veralgemeend: Als de kleuren van sommige gebieden in een kaart vooraf zijn gekozen, wordt het onmogelijk om de overige gebieden zo te kleuren dat in totaal slechts vier kleuren worden gebruikt. Iemand die het tegenvoorbeeld controleert, denkt misschien niet dat het nodig kan zijn om de kleur van deze gebieden te veranderen. Hierdoor lijkt het tegenvoorbeeld geldig, hoewel het dat niet is.
Misschien is een van de gevolgen van deze algemene misvatting dat de kleurbeperking niet transitief is: een gebied hoeft alleen anders gekleurd te worden dan gebieden die het direct raakt, niet gebieden die gebieden raken die het zelf raakt. Als dit de beperking was, zouden voor vlakke grafieken willekeurig veel kleuren nodig zijn.
Andere valse bewijzen schenden de veronderstellingen van de stelling op onverwachte manieren, zoals het gebruik van een gebied dat meerdere losgekoppelde delen heeft, of het niet toestaan dat gebieden van dezelfde kleur elkaar in een punt raken.
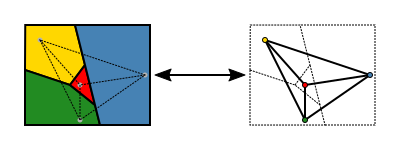
De kaart (links) is gekleurd met vijf kleuren, en het is noodzakelijk om ten minste vier van de tien gebieden te wijzigen om een kleuring met slechts vier kleuren te verkrijgen (rechts).
Kleuren van politieke kaarten
In het echte leven hebben veel landen exclaves of kolonies. Omdat ze bij het land horen, moeten ze met dezelfde kleur worden ingekleurd als het moederland. Dit betekent dat er meestal meer dan vier kleuren nodig zijn om zo'n kaart in te kleuren. Als wiskundigen het hebben over de grafiek die bij het probleem hoort, zeggen ze dat die niet vlak is. Hoewel het gemakkelijk is om te controleren of een grafiek planair is, is het heel moeilijk om het kleinste aantal kleuren te vinden dat nodig is om de grafiek in te kleuren. Het is NP-compleet, een van de moeilijkste problemen die er bestaan. Het kleinste aantal kleuren dat nodig is om een grafiek te kleuren, staat bekend als het chromatische getal. Veel van de problemen die zich voordoen wanneer men probeert de stelling van vier kleuren op te lossen, houden verband met discrete wiskunde. Daarom worden vaak methoden uit de algebraïsche topologie gebruikt.
Uitbreiding naar "niet-vlakke" kaarten
De stelling van de vier kleuren vereist dat de "kaart" zich op een plat vlak bevindt, wat wiskundigen een vlak noemen. In 1890 creëerde Percy John Heawood het zogenaamde Heawood-conject: Het stelt dezelfde vraag als het vierkleurentheorema, maar dan voor elk topologisch object. Een torus kan bijvoorbeeld met maximaal zeven kleuren worden gekleurd. Het Heawood-conject geeft een formule die werkt voor al dergelijke objecten, behalve de Klein-fles.
Vragen en antwoorden
V: Wat is de stelling van vier kleuren?
A: Het vierkleurentheorema is een wiskundige stelling die stelt dat in een vlak oppervlak met regio's de regio's met niet meer dan vier kleuren kunnen worden gekleurd. Aangrenzende gebieden mogen niet dezelfde kleur krijgen.
V: Hoe werd het eerste bewijs van de vierkleurenstelling geleverd?
A: Het eerste bewijs van de vierkleurentheorie was een bewijs door uitputting met 1.936 gevallen. Dit betekent dat het werd vastgesteld door het op te delen in gevallen en elk geval apart te bewijzen.
V: Zijn kaartenmakers geïnteresseerd in dit probleem?
A: Nee, kaartenmakers zijn niet erg geïnteresseerd in dit probleem, omdat kaarten met slechts vier kleuren zeldzaam zijn en meestal slechts drie kleuren nodig hebben. Boeken over cartografie en de geschiedenis van het maken van kaarten maken geen melding van de vierkleuren-eigenschap.
V: Wat is de stelling van vijf kleuren?
A: De stelling van vijf kleuren stelt dat vijf kleuren voldoende zijn om een kaart te kleuren en er is een kort, elementair bewijs voor dat aan het eind van de 19e eeuw werd bewezen.
V: Hoe moeilijk was het om te bewijzen dat slechts 4 kleuren nodig waren voor het kleuren van kaarten?
A: Het bewijzen dat er slechts 4 kleuren nodig zijn voor het kleuren van kaarten bleek veel moeilijker dan verwacht, aangezien er sinds de eerste verklaring in 1852 veel valse bewijzen en valse tegenvoorbeelden zijn verschenen.
V: Is er een voorbeeld van een kaart waar 5 of meer kleuren nodig zijn om alle gebieden goed te kleuren?
A: Ja, zo'n voorbeeld is wanneer een regio wordt omgeven door een oneven aantal andere regio's die elkaar in een cyclus raken - in dat geval kunnen 5 of meer kleuren nodig zijn om alle regio's goed te kleuren.
Zoek in de encyclopedie

