Wiskunde

Wiskunde is de studie van getallen, vormen en patronen. Het woord komt van het Griekse woord "μάθημα" (máthema), wat "wetenschap, kennis of leren" betekent, en wordt soms afgekort tot wiskunde (in Engeland, Australië, Ierland en Nieuw-Zeeland) of wiskunde (in de Verenigde Staten en Canada). De korte woorden worden vaak gebruikt voor rekenkunde, meetkunde of eenvoudige algebra door leerlingen en hun scholen.

De wiskunde omvat de studie van:

Getallen: hoe de dingen kunnen worden geteld.
Structuur: hoe de dingen zijn georganiseerd. Dit subveld wordt meestal algebra genoemd.
Plaats: waar de dingen zich bevinden en hun ordening. Dit subveld wordt meestal geometrie genoemd.
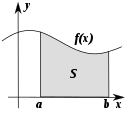
Veranderen: hoe de dingen anders worden. Dit subveld wordt meestal analyse genoemd.

Wiskunde is nuttig voor het oplossen van problemen die zich in de echte wereld voordoen, dus veel mensen studeren en gebruiken naast wiskundigen ook wiskunde. Vandaag de dag is wat wiskunde nodig in veel banen. Mensen die in het bedrijfsleven, de wetenschap, de techniek en de bouw werken, hebben enige kennis van wiskunde nodig.

Probleemoplossing in de wiskunde

De wiskunde lost problemen op door gebruik te maken van logica. Een van de belangrijkste instrumenten van de logica die wiskundigen gebruiken is deductie. Aftrekken is een speciale manier van denken om nieuwe waarheden te ontdekken en te bewijzen met behulp van oude waarheden. Voor een wiskundige is de reden dat iets waar is (een bewijs genoemd) net zo belangrijk als het feit dat het waar is, en deze reden wordt vaak gevonden met behulp van deductie. Het gebruik van deductie is wat het denken over wiskunde anders maakt dan andere soorten wetenschappelijk denken, die zich zouden kunnen baseren op experimenten of op interviews.

Logica en redenering worden door wiskundigen gebruikt om algemene regels te maken, die een belangrijk onderdeel vormen van de wiskunde. Deze regels laten informatie weg die niet belangrijk is, zodat één enkele regel vele situaties kan dekken. Door het vinden van algemene regels lost de wiskunde veel problemen op, terwijl deze regels ook voor andere problemen gebruikt kunnen worden. Deze regels kunnen stellingen genoemd worden (als ze bewezen zijn) of vermoedens (als het nog niet bekend is of ze waar zijn). De meeste wiskundigen gebruiken niet-logische en creatieve redeneringen om een logisch bewijs te vinden.

Soms vindt en bestudeert de wiskunde regels of ideeën die we nog niet begrijpen. Vaak worden in de wiskunde ideeën en regels gekozen omdat ze als eenvoudig of netjes worden beschouwd. Aan de andere kant worden deze ideeën en regels soms in de echte wereld gevonden nadat ze in de wiskunde zijn bestudeerd; dit is in het verleden al vele malen gebeurd. In het algemeen kan het bestuderen van de regels en ideeën van de wiskunde ons helpen om de wereld beter te begrijpen. Enkele voorbeelden van wiskundeproblemen zijn optellen, aftrekken, vermenigvuldigen, delen, rekenen, fracties en decimalen. Algebraproblemen worden opgelost door bepaalde variabelen te evalueren. Een rekenmachine beantwoordt elk wiskundeprobleem in de vier rekenkundige basisbewerkingen.

Studiegebieden in de wiskunde

Aantal

Het is een tak van de wetenschap die zich bezighoudt met de logica van vorm, kwantiteit en ordening. De meeste van de hieronder genoemde gebieden worden bestudeerd in veel verschillende gebieden van de wiskunde, met inbegrip van de set-theorie en de wiskundige logica. De studie van de getaltheorie richt zich meestal meer op de structuur en het gedrag van de gehele getallen dan op de werkelijke fundamenten van de getallen zelf, en is dus niet opgenomen in deze subsectie.

0 , 1 , 2 , 3 , ... 0,1,2,3,3,00 $0,1,2,3,\ldots$	... , - 1 , 0 , 1 , ... {\\\\ldots , -1,0,1,1,\ldots } $\ldots ,-1,0,1,\ldots$	1 2 , 2 3 , 0,125 , ... {\frac {2},{\frac {3}},0,125,{\frac },0,125,{\frac } ${\frac {1}{2}},{\frac {2}{3}},0.125,\ldots$	π , e , 2 , ... {\\\pi , e , e , \rt {\an5}, {\an5}, {\\an5} $\pi ,e,{\sqrt {2}},\ldots$	1 + i , 2 e i π / 3 , ... {\\pi /3},\ldots } $1+i,2e^{i\pi /3},\ldots$
Natuurlijke getallen	Integers	Rationele cijfers	Echte aantallen	Complexe getallen
0 , 1 , ... , ω , ω + 1 , ... , 2 ω , ... {\\omega, \omega, \omega +1,\ldots, 2\omega, \ldots } $0,1,\ldots ,\omega ,\omega +1,\ldots ,2\omega ,\ldots$	ℵ 0 , ℵ 1 , ... {\\\\aleph _0},\aleph _1,\ldots } $\aleph _{0},\aleph _{1},\ldots$	+ , - , × , ÷ {\\\\\\div } $+,-,\times ,\div$	> , ≥ , = , ≤ , < {\\\\geq,=,\leq,< } $>,\geq ,=,\leq ,<$	f ( x ) = x {\displaystyle f(x)={sqrt {x}} $f(x)={\sqrt {x}}$
Gewone nummers	Kardinale nummers	Rekenkundige bewerkingen	Rekenkundige verhoudingen	Functies

Structuur

Veel gebieden van de wiskunde bestuderen de structuur die een object heeft. De meeste van deze gebieden maken deel uit van de studie van algebra.


Getalentheorie	Abstracte algebra	Lineaire algebra	Ordertheorie	Grafiektheorie

Vorm

Sommige gebieden van de wiskunde bestuderen de vormen van de dingen. De meeste van deze gebieden maken deel uit van de studie van de geometrie.


Topologie	Geometrie	Trigonometrie	Differentiaalmeetkunde	Fractale meetkunde

Verander

Sommige gebieden van de wiskunde bestuderen de manier waarop dingen veranderen. De meeste van deze gebieden maken deel uit van de studie van de analyse.


Berekening	Vectorrekening	Analyse

Differentiaalvergelijkingen	Dynamische systemen	Chaostheorie

Toegepaste wiskunde

Toegepaste wiskunde gebruikt wiskunde om problemen op te lossen op andere gebieden zoals techniek, natuurkunde en informatica.

Numerieke analyse - Optimalisatie - Waarschijnlijkheidstheorie - Statistieken - Wiskundige financiën - Speltheorie - Wiskundige natuurkunde - Vloeistofdynamica - Rekenalgoritmen

Beroemde stellingen

Deze stellingen hebben geïnteresseerde wiskundigen en mensen die geen wiskundigen zijn.

Pythagoreïsche stelling - Fermat's laatste stelling - Goldbachs gissing - Twin Prime Conjecture - Gödel's onvolledige stellingen - Poincaré gissing - Cantor's diagonale argument - Vier kleuren stelling - Zorn's lemma - Euler's Identiteit - Kerk-Turing thesis

Dit zijn stellingen en vermoedens die de wiskunde sterk hebben veranderd.

Riemann-hypothese - Continuüm-hypothese - P Versus NP - Pythagoreïsche stelling - Centrale limietstelling - Fundamentele stelling van de calculus - Fundamentele stelling van de algebra - Fundamentele stelling van de rekenkunde - Fundamentele stelling van de projectieve meetkunde - classificatie stellingen van oppervlakken - Gauss-Bonnet stelling - Fermat's laatste stelling - Kantorovitsj stelling

Grondslagen en methoden

De vooruitgang in het begrijpen van de aard van de wiskunde heeft ook invloed op de manier waarop wiskundigen hun onderwerp bestuderen.

Wiskundefilosofie - Wiskundige intuïtie - Wiskundig constructivisme - Grondslagen van de wiskunde - Set-theorie - Symbolische logica - Modeltheorie - Categorie theorie - Logica - Omgekeerde wiskunde - Tabel met wiskundige symbolen

Geschiedenis en de wereld van de wiskundigen

Wiskunde in de geschiedenis, en de geschiedenis van de wiskunde.

Geschiedenis van de wiskunde - Tijdlijn van de wiskunde - Wiskundigen - Veldmedaille - Abelprijs - Millenniumprijs Problemen (Clay MathPrijs) - Internationale wiskundevereniging - Wiskundewedstrijden - Zijdelings denken - Wiskunde en geslacht

Onderscheidingen in de wiskunde

Er is geen Nobelprijs in de wiskunde. Wiskundigen kunnen de Abelprijs en de Fields Medal voor belangrijke werken in ontvangst nemen.

Het Clay Mathematics Institute heeft gezegd dat het een miljoen dollar zal geven aan iedereen die een van de problemen met de Millenniumprijs oplost.

Wiskundige hulpmiddelen

Er zijn veel hulpmiddelen die gebruikt worden om wiskunde te doen of om antwoorden te vinden op wiskundeproblemen.

Oudere gereedschappen

Abacus
Napier's botten, schuifregel
Heerser en Kompas
Mentale berekening

Nieuwer gereedschap

Rekenmachines en computers
Programmeertaal
Computer algebra systemen (lijst)
Internetkortetermijnnotatie
software voor statistische analyse (bijvoorbeeld SPSS)
SAS-programmeertaal
R-programmeertaal

Zie ook

Tijdslijn van vrouwen in de wiskunde
Amerikaanse samenleving voor wiskunde
Maatschappij voor Industriële en Toegepaste Wiskunde
Wiskunde Genealogie Project
Wiskunde Onderwerp Classificatie

Vragen en antwoorden

V: Wat is wiskunde?

A: Wiskunde is de studie van getallen, vormen en patronen. Het woord komt van het Griekse woord μάθημα (máthema), dat "wetenschap, kennis of leren" betekent.

V: Wat zijn de belangrijkste gebieden van de wiskunde?

Antwoord: De belangrijkste gebieden van de wiskunde zijn getallen, structuur (algebra), plaats (meetkunde) en verandering (analyse).

V: Hoe wordt wiskunde in de echte wereld gebruikt?

A: Toegepaste wiskunde is nuttig voor het oplossen van problemen in de echte wereld. Mensen die werkzaam zijn in het bedrijfsleven, de wetenschap, de techniek en de bouw gebruiken wiskunde.

V: Bestaat er een verkorte versie van "wiskunde"?

A: Ja - het kan worden afgekort tot "maths" in de landen van het Britse Gemenebest of "math" in Noord-Amerika.

V: Wat betekent het woord "wiskunde"?

Antwoord: Het woord "wiskunde" komt van het Griekse woord μάθημα (máthema), dat "wetenschap, kennis of leren" betekent.

V: Wat voor soort probleemoplossing houdt toegepaste wiskunde in?

A: Toegepaste wiskunde betreft het oplossen van reële problemen waarmee mensen die werkzaam zijn in het bedrijfsleven, de wetenschap, de techniek en de bouw te maken krijgen.