Holland's schematheorema

Beschrijving

Beschouw binaire strings van lengte 6. Het schema 1*10*1 beschrijft de verzameling van alle strings van lengte 6 met 1's op positie 1, 3 en 6 en een 0 op positie 4. De * is een wildcard symbool, wat betekent dat posities 2 en 5 de waarde 1 of 0 kunnen hebben. De volgorde van een schema o ( H ) {Displaystyle o(H)} is gedefinieerd als het aantal vaste posities in het sjabloon, terwijl de definiërende lengte δ ( H ) {Displaystyle o(H)} de afstand is tussen de eerste en de laatste specifieke positie. De orde van 1*10*1 is 4 en de definiërende lengte is 5. De fitness van een schema is de gemiddelde fitness van alle strings die aan het schema voldoen. De fitness van een string is een maat voor de waarde van de gecodeerde probleemoplossing, zoals berekend door een probleemspecifieke evaluatiefunctie. Gebruikmakend van de gevestigde methoden en genetische operatoren van genetische algoritmen, stelt het schema theorema dat korte, lage-orde schema's met een bovengemiddelde fitness exponentieel toenemen in opeenvolgende generaties. Uitgedrukt als een vergelijking:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {E} (m(H,t+1))≥ {m(H,t)f(H) ≥ a_{t}}[1-p]. }

Hierin is m ( H , t ) {\displaystyle m(H,t)} het aantal strings dat behoort tot schema H {\displaystyle H} bij generatie t {\displaystyle t} f ( H ) {\displaystyle f(H)} is de waargenomen gemiddelde fitness van schema H {\displaystyle H} en a t {\displaystyle a_{t}} is de waargenomen gemiddelde fitness op generatie t {\displaystyle t} . De verstoringskans p {{\displaystyle p}} is de kans dat door kruising of mutatie het schema H {\displaystyle H}} wordt vernietigd. Deze kan worden uitgedrukt als:

p = δ ( H ) l - 1 p c + o ( H ) p m {Displaystyle p={delta (H) over l-1}p_{c}+o(H)p_{m}}

waarbij o ( H ) {\displaystyle o(H)} de volgorde van het schema is, l {\displaystyle l} de lengte van de code is, p m {\displaystyle p_{m}} de mutatiekans is en p c {\displaystyle p_{c}} de crossover-kans is. Een schema met een kortere definiërende lengte δ ( H ) {\displaystyle \delta (H)} heeft dus minder kans om verstoord te worden.
Een vaak verkeerd begrepen punt is waarom de Schema Theorema een ongelijkheid
is in plaats van een gelijkheid. Het antwoord is in feite eenvoudig: de Stelling verwaarloost de kleine, maar niet nul, kans dat een snaar die behoort tot het schema H {{Displaystyle H}} "from scratch" ontstaat door mutatie van een enkele snaar (of recombinatie van twee snaren) die in de vorige generatie niet tot H {{Displaystyle H}} behoorde.

Beperking

De schematheorema geldt onder de aanname van een genetisch algoritme dat een oneindig grote populatie in stand houdt, maar gaat niet altijd op voor de (eindige) praktijk: als gevolg van steekproeffouten in de initiële populatie kunnen genetische algoritmen convergeren naar schema's die geen selectief voordeel hebben. Dit gebeurt met name bij multimodale optimalisatie, waar een functie meerdere pieken kan hebben: de populatie kan afdrijven naar de voorkeur voor één van de pieken, en de andere negeren.

De reden dat de Schema Theorie de kracht van genetische algoritmen niet kan verklaren, is dat zij geldt voor alle probleemgevallen, en geen onderscheid kan maken tussen problemen waarbij genetische algoritmen slecht presteren, en problemen waarbij genetische algoritmen goed presteren.

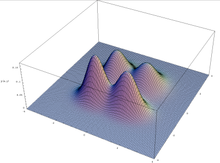
Uitzetten van een multimodale functie in twee variabelen.