Newton's bewegingswetten
Isaac Newton (1642-1727) is algemeen bekend als de vader van de dynamica, de studie van de beweging. Hij ontwikkelde drie wetten die de basis vormen van de klassieke mechanica. Zij worden voor waar aangenomen omdat de resultaten van experimenten door wetenschappers overeenkomen met zijn wetten.
Oorspronkelijke publicatie van de eerste twee wetten, in het Latijn
Eerste wet
- Als een lichaam in rust is, blijft het in rust of, als het in beweging is, beweegt het met gelijke snelheid, totdat er een nettokracht op wordt uitgeoefend.
Een "uniforme snelheid" betekent dat een voorwerp met een constante snelheid beweegt zonder van richting te veranderen (d.w.z. in een rechte lijn). Een "nettokracht" betekent dat de krachten die op het voorwerp werken niet in evenwicht zijn. Met andere woorden, de eerste wet stelt twee dingen:
- Een stilstaand voorwerp beweegt alleen als er een onevenwichtige kracht op werkt.
- Een bewegend voorwerp verandert alleen van snelheid of richting als er een onevenwichtige kracht op werkt.
In het eerste deel staat dat een tafel die op de grond rust niet beweegt tenzij hij wordt geduwd. Hoewel de zwaartekracht op de tafel werkt en hem naar beneden trekt, is er een reactiekracht van de grond die hem terugduwt. De krachten die op de tafel werken zijn in evenwicht, dus zal het voorwerp niet bewegen.
Het tweede deel is moeilijker te begrijpen. Een bal die over een plat oppervlak rolt, zal vertragen en uiteindelijk tot stilstand komen. Maar dat komt door wrijving, een kracht die de bal afremt. Een bal die van een helling afrolt heeft ook te maken met wrijving, maar de zwaartekracht die hem in beweging brengt is sterker. Op een plaats zonder de krachten van wrijving, luchtweerstand en zwaartekracht (bijvoorbeeld in de ruimte) zou een bewegend voorwerp in een rechte lijn blijven bewegen als er geen kracht was om het af te remmen of van richting te veranderen.
Tweede wet
- Voor een deeltje met massa m is de nettokracht F op het deeltje gelijk aan de massa m maal de versnelling a van het deeltje:
F = m a {\mathbf {F} =mathbf {a} } 
.
Volgens de tweede wet van Newton is de versnelling van een deeltje afhankelijk van de krachten die op het deeltje werken en de massa van het deeltje. Voor een gegeven deeltje neemt de versnelling toe als de nettokracht toeneemt. Hoe meer massa een deeltje heeft bij een gegeven nettokracht, hoe minder versnelling het heeft.
Gewicht is bijvoorbeeld een kracht die wij op aarde voelen, veroorzaakt door de zwaartekracht. Het gewicht W op een deeltje wordt gegeven door
W = m g {\mathbf {W} =mathbf {g} } 
,
waarbij m de massa van het deeltje is en g de plaatselijke gravitatieversnelling (niet te verwarren met G, de universele gravitatieconstante), ruwweg gelijk aan 9,8 meter per seconde2 (32 voet per seconde2 ) op aarde.
We kunnen de tweede wet van Newton uitdrukken in termen van impuls. Het momentum p van een deeltje wordt gedefinieerd als het product van zijn massa m en zijn snelheid v:
p = m v {{mathbf {p} =mathbf {v}}. 
.
De versnelling a van een deeltje is de tijdsafgeleide van zijn snelheid v:
a = d v d t {\mathbf {a} ={frac {mathrm {d} \mathbf {v} } }
.
Daarom,
F = m a = m d v d t = d ( m v ) d t = d p d t {\displaystyle \mathbf {F} = m mathbf {a} =m{frac {mathrm {d} \mathbf {v}{{mathrm {d} t}}={frac {mathrm {d} (m\mathbf {v} )}{mathrm {d} t}}={frac {mathrm {d} \mathbf {p} } }
.
We hebben dus een andere manier om de tweede wet van Newton te formuleren:
- Voor een deeltje met massa m is de nettokracht F op het deeltje gelijk aan de tijdsafgeleide van de impuls p van het deeltje:
F = d p d t {F} ={frac {mathrm {d} \mathbf {p} } }
.
In de klassieke mechanica zijn de twee vormen van de tweede wet, F = m a {mathbf {F} =mathbf {a} en F = d p d t. \mathbf {p} }{\mathrm {d} t}}}. zijn volledig gelijkwaardig. Merk op dat we aannemen dat de massa m van een deeltje niet verandert.
Derde wet
- Voor elke actie is er een gelijke en tegengestelde reactie. Of elke actie reageert altijd in de tegenovergestelde richting.
Dit is het beste te begrijpen aan de hand van biljartballen, waar je gemakkelijk de actie/reactie-paren van krachten kunt zien. Als je tegen een voetbal trapt, beweegt niet alleen de bal, maar voel je ook een kracht op je voet.
De grootte van de krachten op het eerste voorwerp is gelijk aan de grootte van de kracht op het tweede voorwerp. De richting van de kracht op het eerste voorwerp is tegengesteld aan de richting van de kracht op het tweede voorwerp. Krachten komen altijd in paren - gelijke en tegengestelde actie-reactie krachtparen.
Een verscheidenheid van actie-reactie krachtparen is duidelijk in de natuur. Denk aan de voortbeweging van een vis door het water. Een vis gebruikt zijn vinnen om het water naar achteren te duwen. Maar een duw op het water zal alleen dienen om het water te versnellen. Aangezien krachten het gevolg zijn van wederzijdse interacties, moet het water de vis ook vooruit duwen, waardoor de vis door het water wordt voortgestuwd. De grootte van de kracht op het water is gelijk aan de grootte van de kracht op de vis; de richting van de kracht op het water (achteruit) is tegengesteld aan de richting van de kracht op de vis (vooruit). Voor elke actie is er een gelijke (in grootte) en tegengestelde (in richting) reactiekracht. Door actie-reactiekrachtenparen kunnen vissen zwemmen.
Denk aan de beweging van een auto op weg naar school. Een auto heeft wielen die vooruit draaien. Wanneer de wielen vooruit draaien, grijpen ze in de weg en duwen ze de weg naar achteren. Aangezien krachten het resultaat zijn van wederzijdse interacties, moet de weg de wielen ook naar voren duwen. De grootte van de kracht op de weg is gelijk aan de grootte van de kracht op de wielen (of de auto); de richting van de kracht op de weg (achteruit) is tegengesteld aan de richting van de kracht op de wielen (vooruit). Voor elke actie is er een gelijke (in grootte) en tegengestelde (in richting) reactie. Door actie-reactiekrachtenparen kunnen auto's over een wegdek rijden.
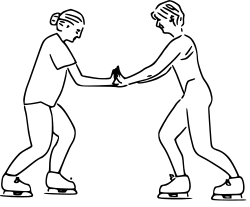
De derde wet van Newton. De krachten van de schaatsers op elkaar zijn even groot, en in tegengestelde richting
