Kans (kansrekening)
Waarschijnlijkheid is een onderdeel van toegepaste wiskunde. Het heeft te maken met toeval, de studie van dingen die wel of niet kunnen gebeuren.
Met behulp van de waarschijnlijkheid kun je bijvoorbeeld laten zien dat als je een muntstuk in de lucht gooit en laat landen, het de helft van de tijd zal landen met de ene kant naar boven, en de helft van de tijd met de andere kant naar boven. Veel munten hebben een afbeelding van het gezicht van een beroemd persoon aan de ene kant, en iets anders aan de andere kant. Vaak noemen mensen de kant met het gezicht "hoofden", en de andere kant "staarten".
De kans (p) op een gebeurtenis ligt altijd tussen nul (onmogelijk) en één (zeker).
Als we een dobbelsteen gooien (meervoud: dobbelstenen), dan is de kans dat hij op 1 komt 1/6 (dit komt omdat er 6 getallen op een dobbelsteen staan). Ook is de kans dat de dobbelsteen op 2 komt 1/6. Dit komt omdat het op 1, 2, 3, 4, 5 of 6 kan landen. De kans dat een getal tussen 1 en 6 landt is 1. Elke keer als we de dobbelsteen gooien, zal het altijd op een getal tussen 1 en 6 landen.
Waarschijnlijkheid kan worden bepaald met behulp van wiskunde. Als je bijvoorbeeld met zes dobbelstenen gooit, is de kans dat je een getal meer dan tien krijgt niet vanzelfsprekend, maar kan dit met behulp van wiskunde en wetenschap worden uitgezocht.
Een van de meest interessante dingen over toeval is dat om de waarschijnlijkheid te achterhalen dat twee dingen allebei gebeuren, je hun twee waarschijnlijkheden samen vermenigvuldigt. Stel dat u bijvoorbeeld de kans wilt weten dat u twee dobbelstenen gooit en een bepaalde combinatie krijgt (het kan twee 6s zijn of een 3 en dan een 5, gewoon twee). De mogelijkheid om een 3 te krijgen is één op zes (⅙) en de mogelijkheid om een 5 te krijgen is ook één op zes, dus de kans om een 3 dan een 5 te krijgen is ⅙×⅙=⅟36. Als dat getal wordt uitgedrukt als ergens tussen 0 en 1, is het gelijk aan 0,027...7, wat vrij laag is. De mogelijkheid om een 3 te krijgen, dan een 5, en dan een 2 zou ⅙×⅙×⅙=⅟216 of 0.00463 zijn, wat een veel lagere kans is.
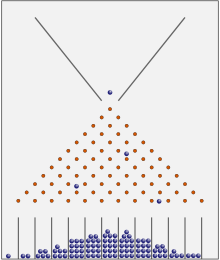
In een bonenmachine of Galton-doos komen de meeste ballen dicht bij het centrum terecht. Op de lange termijn zullen ze een normale verdeling laten zien...
Kansberekening
Mensen als Jacob Bernoulli, Pierre-Simon Laplace of Christiaan Huygens gebruikten het woord waarschijnlijkheid, zoals hierboven beschreven. Andere mensen dachten aan frequenties; het begrip waarschijnlijkheid wordt meestal Frequentie waarschijnlijkheid genoemd.
Gerelateerde pagina's
- Lijst van wiskundige onderwerpen
- Waarschijnlijkheidstheorie
Zoek in de encyclopedie