Rechter- en linkerhandregel: uitleg van het kruisproduct in vectoren
Leer de rechter- en linkerhandregel voor het kruisproduct in vectoren: heldere stap-voor-stap uitleg, visuals en praktische tips om richting en teken foutloos te bepalen.
Rechterhandregel is een conventie in vectorrekenen die je helpt de richting van een kruisproduct (vectorproduct) te bepalen. Het kruisproduct van twee vectoren a en b is een vector c die loodrecht staat op zowel a als b en waarvan de richting wordt gegeven door de rechterhandregel. De grootte van c is |c| = |a| |b| sin(θ), waarbij θ de georiënteerde hoek tussen a en b is.
Hoe gebruik je de rechterhandregel (praktische stappen)
- Sluit je rechterhand en steek twee vingers uit die onder een hoek van 90° staan.
- Een veelgebruikte methode is: wijs je wijsvinger in de richting van de eerste vector (a), wijs je middelvinger in de richting van de tweede vector (b) en dan wijst je duim in de richting van a×b.
- In sommige uitleg (zoals in de oorspronkelijke korte instructie hieronder) gebruik je je duim voor de eerste vector en je wijsvinger voor de tweede; je middelvinger geeft dan de richting van het kruisproduct aan. Beide methodes zijn hetzelfde, zolang je consistent de volgorde van de vingers behoudt.
Een eenvoudig stappenplan (variatie die veel mensen herkennen):
- Steek je wijsvinger en middelvinger zo uit dat ze haaks op elkaar staan.
- Wijs je wijsvinger in de richting van de eerste vector.
- Wijs je middelvinger in de richting van de tweede vector.
- Je duim staat nu in de richting van het kruisproduct (a×b).
Vermijd verwarring: als je de volgorde van de vectoren verwisselt (b×a in plaats van a×b), wijst het resultaat in de tegengestelde richting. Formeel geldt:
- Anticommutativiteit: a × b = −(b × a)
- Perpendiculariteit: a × b staat loodrecht op zowel a als b
- Magnitude: |a × b| = |a| |b| sin(θ)
- Parallelle vectoren: als a en b evenwijdig (of tegenrichting) zijn, dan is a × b = 0
Voorbeelden
In een rechtshandig cartesisch assenstelsel met eenheden i, j, k geldt:
- i × j = k
- j × k = i
- k × i = j
- En omgekeerd: j × i = −k, enz.
Linkerhandregel en andere regels
De term linkerhandregel verschijnt soms in de praktijk, bijvoorbeeld bij bepaalde engineeringmnemotechnieken (zoals Fleming's linker- of rechterhandregels) of wanneer men in een linkerhandsysteem werkt. Wiskundig volgt het kruisproduct echter altijd de rechterhandoriëntatie; als je de linkerhand gebruikt, krijg je de tegengestelde richting. Let daarom goed op welke conventie of oriëntatie in jouw toepassing wordt gebruikt (bijvoorbeeld bij electronenstroom versus positieve stroom in elektromagnetisme).
Praktische tip
Als je moeite hebt met oriëntaties, werk dan eerst in termen van richtingen en test met bekende basisgevallen (zoals i, j, k). Oefen met eenvoudige voorbeelden: leg i en j uit elkaar en gebruik je handmethode om te controleren dat i × j = k. Zo bouw je vertrouwen op voordat je met willekeurige vectoren rekent.
De rechterhandregel is een conventie in vectorrekenen. Het helpt je de richting te onthouden wanneer vectoren kruiselings worden vermenigvuldigd.
- Begin met het sluiten van je rechterhand en steek je aanwijsvinger uit.
- Steek je duim recht omhoog alsof je het teken voor een pistool maakt.
- Als je je "pistool" recht vooruit richt, steek dan je middelvinger uit zodat deze naar links wijst en al je vingers haaks op elkaar staan.
Als je twee vectoren hebt die je wilt kruisen, kun je de richting van de vector die naar buiten komt berekenen door je duim in de richting van de eerste vector te wijzen en je wijzer in de richting van de tweede vector. Uw middelvinger zal de richting van het kruisproduct aanwijzen.
Vergeet niet dat wanneer je de volgorde waarin de vectoren worden gekruist verandert, het resultaat in de tegenovergestelde richting gaat. Dus het is belangrijk om ervoor te zorgen dat je in de volgorde van de u m b → × p o i n t e r → = m i d d l e {\\\c {duim}} 

De linkshandige oriëntatie wordt links weergegeven, en de rechtshandige rechts.
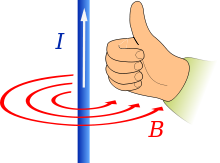
Voorspelling van de richting van het veld (B) wanneer de stroom I in de richting van de duim stroomt

De rechtse regel voor beweging geproduceerd met schroefdraad
Variaties
Er is nog een andere regel die de rechterhandregel (of kurkentrekkerregel) wordt genoemd en die wordt gebruikt voor magnetische velden en dingen die ronddraaien.
1. Begin met het platleggen van je rechterhand en richt je duim recht naar buiten, zodat deze in een rechte hoek staat ten opzichte van je andere vingers.
2. Krul nu je vingers in een vuist en houd je duim uit (als een Thumbs Up).
3. Zorg ervoor dat je vingers in de juiste verhouding staan tot de manier waarop iets beweegt. De richting waarin je duim wijst is de richting van de vector die we gebruiken om erover te praten.
U kunt dit in omgekeerde richting doen door uw duim in de richting van de vector te bewegen en te zien hoe uw vingers omkrullen om de draairichting te zien. Als u uw duim in de richting van de stroom in een draad wijst, is het magnetisch veld dat er omheen komt in de richting van uw krullende vingers.
Vragen en antwoorden
V: Wat is de rechterhandregel?
A: De rechterhandregel is een conventie in vectorwiskunde die u helpt de richting te onthouden wanneer vectoren kruiselings worden vermenigvuldigd.
V: Hoe gebruikt u de rechterhandregel om de richting van een kruisproduct te bepalen?
Antwoord: Om de richting van een kruisproduct te bepalen, sluit u uw rechterhand en steekt u uw wijsvinger uit. Steek uw duim recht omhoog alsof u het teken voor een pistool maakt. Richt uw "pistool" recht vooruit, steek vervolgens uw middelvinger uit zodat deze naar links wijst en al uw vingers haaks op elkaar staan. Richt uw duim in de richting van de eerste vector en richt uw wijsvinger in de richting van de tweede vector. Uw middelvinger wijst in de richting van het kruisproduct.
V: Wat gebeurt er als u de volgorde verandert wanneer vectoren gekruist worden?
Antwoord: Als u bij een kruiselingse vermenigvuldiging van vectoren van volgorde verandert, gaat het resultaat in tegengestelde richting. Daarom is het belangrijk dat u de volgorde van duim x wijzer = midden aanhoudt.
V: Wat betekent deze vergelijking? {Displaystyle {duim}} maal {pointer}}= {midden}} .
Antwoord: Deze vergelijking betekent dat als twee vectoren gekruist met elkaar worden vermenigvuldigd (duim x wijzer), er een derde vector (midden) ontstaat.
Zoek in de encyclopedie