Wet van Snellius
De brekingswet van Snell is de wetenschappelijke wet van de breking van licht of andere golven. In de optiek gaat de wet van Snell over de snelheid van het licht in verschillende media. De wet stelt dat wanneer licht door verschillende materialen gaat (bijvoorbeeld van lucht naar glas) de verhouding tussen de sinussen van de invalshoek (inkomende hoek) en de brekingshoek (uitgaande hoek) niet verandert:
zonde θ 1 zonde θ 2 = v 1 v 2 = n 2 n 1 {\frac {\frac {sin \\1}}={\frac {v_1}{v_{2}}={\frac {n_{2}}} 
Met elke θ {displaystyle \theta } 
als de hoek gemeten vanaf de normaal van de grens, v {displaystyle v}
als de snelheid van het licht in het betreffende medium (SI-eenheden zijn meters per seconde, of m/s). n {displaystyle n} 
is de brekingsindex van het medium.
De brekingsindex van een vacuüm is 1 en de lichtsnelheid in een vacuüm is c {displaystyle c}
. Als een golf het materiaal passeert waar de brekingsindex n is, wordt de snelheid van de golf c n {displaystyle {c}{n}}. 
.
De wet van Snell kan worden bewezen door het principe van Fermat. Het principe van Fermat stelt dat licht de weg aflegt die het minst lang duurt.
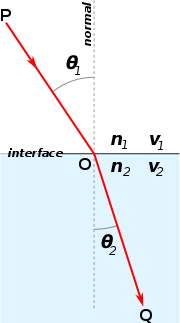
Breking van het licht op het grensvlak tussen twee media met verschillende brekingsindexen, met n2 > n1
Een lichtstraal raakt een glazen prisma en is gebroken...
Geschiedenis
Het idee heeft een lange geschiedenis. Het probleem had de aandacht van Held van Alexandrië, Ptolemaeus, Ibn Sahl en Huygens. Ibn Sahl ontdekte eigenlijk de wet van de breking. In Traité de la Lumiere, 1678, liet Huygens zien hoe de sinuswet van Snell kon worden verklaard door, of afgeleid van, de golfkarakteristiek van het licht.
Vragen en antwoorden
V: Wat is de brekingswet van Snell?
A: De brekingswet van Snell is de wetenschappelijke wet van de breking van licht of andere golven. In de optica stelt deze wet dat wanneer licht door verschillende materialen gaat, de verhouding tussen de sinus van de invals- en brekingshoek niet verandert.
V: Hoe kan de Wet van Snell worden bewezen?
A: De Wet van Snell kan worden bewezen met het principe van Fermat, dat stelt dat licht de weg volgt die de minste tijd vergt.
V: Wat is het principe van Fermat?
A: Het principe van Fermat stelt dat licht langs de weg reist die de minste tijd kost.
V: Wat zijn n en v in de wet van Snell?
A: n is de brekingsindex van een medium en v is de snelheid van het licht in het betreffende medium (gemeten in meters per seconde).
V: Wat betekent c in de Wet van Snell?
A: c staat voor de snelheid van licht in een vacuüm, dat een brekingsindex van 1 heeft.
V: Hoe berekent u de snelheid wanneer een golf door een materiaal met brekingsindex n gaat?
Antwoord: De snelheid wordt c/n wanneer een golf door een materiaal met brekingsindex n gaat.
