Lichtsnelheid

Voorbeeld

Dit gedrag is anders dan onze gebruikelijke ideeën over beweging, zoals dit voorbeeld laat zien:

George staat op de grond naast enkele treinsporen (spoorlijn). Er is een trein die met 48 km/u voorbij rijdt. George gooit een honkbal met 140 km/u in de richting van de trein. Tom, een passagier in de trein, heeft een apparaat (zoals een radarpistool) om werpsnelheden te meten. Omdat hij op de trein zit, beweegt Tom al met 48 km/u in de richting van de worp, dus Tom meet de snelheid van de bal als slechts 60 km/u (97 km/u).

Met andere woorden, de snelheid van het honkbal, zoals gemeten door Tom op de trein, is afhankelijk van de snelheid van de trein.

In het bovenstaande voorbeeld bewoog de trein met 1/3 van de snelheid van de bal, en de snelheid van de bal zoals gemeten op de trein was 2/3 van de werpsnelheid zoals gemeten op de grond.

Nu, herhaal het experiment met licht in plaats van een honkbal; dat wil zeggen, George heeft een zaklamp in plaats van het gooien van een honkbal. George en Tom hebben allebei dezelfde apparaten om de snelheid van het licht te meten (in plaats van het radarpistool in het honkbalvoorbeeld).

George staat op de grond naast enkele treinsporen. Er rijdt een trein met 1/3 van de lichtsnelheid voorbij. George knippert een lichtstraal in de richting van de trein. George meet de lichtsnelheid als 186.282 mijl per seconde (299.792 kilometer per seconde). Tom, een reiziger in de trein, meet de snelheid van de lichtstraal. Welke snelheid meet Tom?

Intuïtief kan men denken dat de snelheid van het licht van de zaklamp zoals gemeten op de trein 2/3 van de snelheid gemeten op de grond moet zijn, net zoals de snelheid van het honkbal 2/3 was. Maar in feite is de snelheid die op de trein wordt gemeten de volledige waarde, 186.282 mijl per seconde (299.792 kilometer per seconde), niet 124.188 mijl per seconde (199.861 kilometer per seconde).

Het klinkt onmogelijk, maar dat is wat men meet. Een deel van de reden is dat licht energie is die op een heel andere manier werkt en beweegt dan materie of vaste objecten zoals een honkbal.

Maxwell's vergelijkingen voorspelden de lichtsnelheid en bevestigden Michael Faraday's idee dat licht een elektromagnetische golf is (een manier waarop energie beweegt). Uit deze vergelijkingen blijkt dat de lichtsnelheid gerelateerd is aan de inverse van de vierkantswortel van de permittiviteit van de vrije ruimte, ε0, en de permeabiliteit van de vrije ruimte, μ0:

c = 1 ε 0 μ 0 . . }

Een gevolg van dit feit is dat niets sneller kan gaan dan de snelheid van het licht. Een ander gevolg is dat voor voorwerpen die massa hebben, het maakt niet uit hoeveel energie er gebruikt wordt om de snelheid van een voorwerp te verhogen, het zal steeds dichterbij komen, maar het zal nooit de snelheid van het licht bereiken. Deze ideeën werden begin 1900 ontdekt door Albert Einstein, wiens werk ons begrip van licht volledig veranderde.

De brekingsindex van een helder materiaal is de verhouding tussen de lichtsnelheid in een vacuüm en de lichtsnelheid in dat materiaal.

Meting

Rømer

Ole Christensen Rømer gebruikte een astronomische meting om de eerste kwantitatieve schatting van de lichtsnelheid te maken. Gemeten vanaf de Aarde zijn de perioden van manen die rond een verre planeet draaien korter als de Aarde de planeet nadert dan wanneer de Aarde zich van de planeet terugtrekt. De afstand die licht van de planeet (of zijn maan) tot de Aarde aflegt is korter als de Aarde op het punt in zijn baan is dat het dichtste bij de planeet is dan als de Aarde op het verste punt in zijn baan is, waarbij het verschil in afstand de diameter van de baan van de Aarde rond de Zon is. De waargenomen verandering in de baanperiode van de maan is eigenlijk het verschil in de tijd die het licht nodig heeft om de kortere of langere afstand te overbruggen. Rømer nam dit effect waar voor de binnenste maan Io van Jupiter, en hij leidde daaruit af dat het licht er 22 minuten over doet om de diameter van de baan van de Aarde te overbruggen.

Bradley

Een andere methode is het gebruik van de aberratie van het licht, ontdekt en uitgelegd door James Bradley in de 18e eeuw. Dit effect is het gevolg van de vectortoevoeging van de snelheid van het licht dat uit een verre bron (zoals een ster) komt en de snelheid van de waarnemer (zie het diagram hiernaast). Een bewegende waarnemer ziet het licht dus uit een iets andere richting komen en ziet dus de bron in een positie die is verschoven ten opzichte van zijn oorspronkelijke positie. Omdat de richting van de snelheid van de Aarde voortdurend verandert als de Aarde rond de Zon draait, zorgt dit effect ervoor dat de schijnbare positie van de sterren verschuift. Vanuit het hoekverschil in de positie van de sterren is het mogelijk om de lichtsnelheid uit te drukken in termen van de snelheid van de aarde rond de zon. Dit kan, met de bekende lengte van een jaar, eenvoudig omgerekend worden naar de tijd die nodig is om van de Zon naar de Aarde te reizen. In 1729 gebruikte Bradley deze methode om af te leiden dat het licht 10.210 keer sneller reisde dan de Aarde in zijn baan (het moderne getal is 10.066 keer sneller) of, gelijkwaardig, dat het licht 8 minuten 12 seconden nodig zou hebben om van de Zon naar de Aarde te reizen.

Moderne

Tegenwoordig wordt de "lichttijd voor eenheidsafstand"-het omgekeerde van c (1/c), uitgedrukt in seconden per astronomische eenheid- gemeten door de tijd te vergelijken die radiosignalen nodig hebben om verschillende ruimteschepen in het Zonnestelsel te bereiken. De positie van een ruimteschip wordt berekend aan de hand van de gravitatie-effecten van de Zon en verschillende planeten. Door veel van zulke metingen te combineren wordt een best passende waarde voor de lichttijd per eenheidsafstand verkregen. Vanaf 2009^[update] is de beste schatting, zoals goedgekeurd door de Internationale Astronomische Unie (IAU):

lichte tijd voor de afstand per eenheid: 499.004783836(10) s

c = 0,00200398880410(4) AU/s

c = 173,144632674(3) AU/dag.

De relatieve onzekerheid in deze metingen is 0,02 deeltjes per miljard (2×10-11), als equivalent van de onzekerheid in aardse lengtemetingen door interferometrie. Aangezien de meter is gedefinieerd als de lengte die door het licht in een bepaald tijdsinterval wordt afgelegd, kan de meting van de lichttijd voor de afstand per eenheid ook worden geïnterpreteerd als het meten van de lengte van een AE in meters. De meter wordt beschouwd als een juiste lengte-eenheid, terwijl de AE vaak wordt gebruikt als een eenheid van geobserveerde lengte in een bepaald referentiekader.

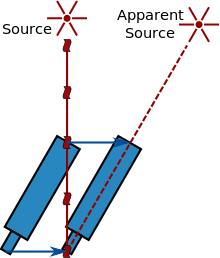
Aberratie van het licht: licht van een verre bron lijkt van een andere plaats te komen voor een bewegende telescoop vanwege de eindige snelheid van het licht.

Praktische effecten

De eindige snelheid van het licht is een belangrijke beperking voor lange-afstandsruimtevaarten. Stel dat er een reis naar de andere kant van de Melkweg zou zijn, dan zou de totale tijd voor een bericht en het antwoord daarop ongeveer 200.000 jaar bedragen. Nog ernstiger is dat geen enkel ruimteschip sneller kan reizen dan het licht, dus al het vervoer op galactische schaal zou effectief eenrichtingsverkeer zijn, en zou veel langer duren dan elke moderne beschaving heeft bestaan.

De snelheid van het licht kan ook op zeer korte afstanden van belang zijn. Bij supercomputers legt de lichtsnelheid een grens op aan de snelheid waarmee gegevens tussen processoren kunnen worden verzonden. Als een processor op 1 gigahertz werkt, kan een signaal maximaal zo'n 30 centimeter (1 ft) in een enkele cyclus afleggen. Processoren moeten daarom dicht bij elkaar worden geplaatst om de communicatielatentie tot een minimum te beperken; dit kan leiden tot problemen met de koeling. Als de klokfrequenties blijven toenemen, zal de snelheid van het licht uiteindelijk een beperkende factor worden voor het interne ontwerp van enkele chips.

Gerelateerde pagina's

• Michelson-Morley-experiment