Eenheidscirkel
In de wiskunde is een eenheidscirkel een cirkel met een straal van 1. De vergelijking van de eenheidscirkel is x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1}
. Het middelpunt van de eenheidscirkel ligt bij de oorsprong, of coördinaten (0,0). Hij wordt vaak gebruikt in Trigonometrie.
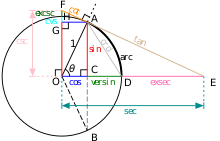
De Eenheidscirkel kan gebruikt worden om elke trigonometrische functie te modelleren.
Trigonometrische functies in de eenheidscirkel
In een eenheidscirkel, waarbij t {\displaystyle t}
de gewenste hoek is, kunnen x {\displaystyle x} 
en y {\displaystyle y}
gedefinieerd worden als cos ( t ) = x {\displaystyle \cos(t)=x}
en sin ( t ) = y {\displaystyle \sin(t)=y}
. Met behulp van de functie van de eenheidscirkel, x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} wordt een andere vergelijking voor de eenheidscirkel gevonden, cos 2 ( t ) + sin 2 ( t ) = 1 {\displaystyle \cos ^{2}(t)+\sin ^{2}(t)=1}
. Bij het werken met goniometrische functies is het vooral handig om hoeken te gebruiken met maten tussen 0 en π 2 {\displaystyle \pi \over 2}
radialen, of 0 tot en met 90 graden. Het is echter ook mogelijk om grotere hoeken te gebruiken. Met behulp van de eenheidscirkel kunnen twee identiteiten gevonden worden: cos ( t ) = cos ( 2 ⋅ π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k+t)} 
en s i n ( t ) = sin ( 2 ⋅ π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k+t)}
voor elk geheel getal k {\displaystyle k}
.
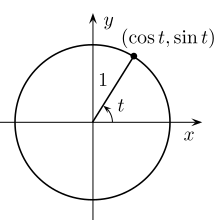
De eenheidscirkel kan variabelen vervangen voor goniometrische functies.
Vragen en antwoorden
V: Wat is een eenheidscirkel?
A: Een eenheidscirkel is een cirkel met een straal van 1.
V: Wat is de vergelijking van de eenheidscirkel?
A: De vergelijking van de eenheidscirkel is x^2 + y^2 = 1.
V: Waar ligt het middelpunt van de eenheidscirkel?
A: Het middelpunt van de eenheidscirkel ligt bij de oorsprong, of coördinaten (0,0).
V: Wat is het doel van de eenheidscirkel in de wiskunde?
A: De eenheidscirkel wordt vaak gebruikt in Trigonometrie.
V: Waarom is de eenheidscirkel belangrijk?
A: De eenheidscirkel is belangrijk omdat hij helpt bij het begrijpen van de relaties tussen hoeken en goniometrische functies.
V: Wat is de straal van de eenheidscirkel?
A: De straal van de eenheidscirkel is 1.
V: Wat betekent het dat de straal van de eenheidscirkel 1 is?
A: Het belang van een straal van de eenheidscirkel van 1 is dat het berekeningen vereenvoudigt en het gemakkelijk maakt om hoeken aan goniometrische waarden te relateren.
