AlegsaOnline.com

Cirkel | een ronde, tweedimensionale vorm

Schrijver: Leandro Alegsa

28-12-2022

Een cirkel is een ronde, tweedimensionale vorm. Alle punten op de rand van de cirkel liggen op dezelfde afstand van het middelpunt.

De straal van een cirkel is een lijn van het middelpunt van de cirkel naar een punt aan de zijkant. Wiskundigen gebruiken de letter r voor de lengte van de straal van een cirkel. Het middelpunt van een cirkel is het punt in het midden. Het wordt vaak geschreven als O $O$ .

De diameter (wat "helemaal" betekent) van een cirkel is een rechte lijn die van de ene kant naar de andere kant en dwars door het middelpunt van de cirkel gaat. Wiskundigen gebruiken de letter d $d$ voor de lengte van deze lijn. De diameter van een cirkel is gelijk aan tweemaal de straal ( d {displaystyle d} $d$ is gelijk aan 2 maal r {displaystyle r} ):

d = 2 r {Displaystyle d=2r} $d=2r$

De omtrek van een cirkel is de lijn die rond het middelpunt van de cirkel loopt. Wiskundigen gebruiken de letter C $C$ voor de lengte van deze lijn.

Het getal π (geschreven als de Griekse letter pi) is een zeer nuttig getal. Het is de lengte van de omtrek gedeeld door de lengte van de diameter ( π {\displaystyle \pi } $\pi$ is gelijk aan C {\displaystyle C} $C$ gedeeld door d {\displaystyle d} $d$ ). Als breuk is het getal π {displaystyle \pi } $\pi$ gelijk aan ongeveer 22 / 7 {displaystyle 22/7} $22/7$ of 355 / 113 {displaystyle 355/113} $355/113$ (wat dichterbij ligt) en als getal is het ongeveer 3,1415926535.

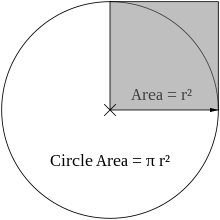
De oppervlakte, A {\an5} $A$ binnen een cirkel is gelijk aan de straal vermenigvuldigd met zichzelf, vervolgens vermenigvuldigd met π {\displaystyle \pi }. $\pi$ ( A {\displaystyle A} $A$ is gelijk aan π {\displaystyle \pi } $\pi$ maal r {\displaystyle r} maal r {\displaystyle r} ).

Berekening van π

π {\displaystyle \pi } $\pi$ kan worden gemeten door een cirkel te tekenen en vervolgens de diameter ( d {\displaystyle d} $d$ ) en de omtrek ( C {\displaystyle C} $C$ ) te meten. Dit komt omdat de omtrek van een cirkel altijd gelijk is aan π {\displaystyle \pi } $\pi$ maal de diameter.

π = C d {{d}}}. $\pi ={\frac {C}{d}}$

π {\displaystyle \pi } $\pi$ kan ook alleen met wiskundige methoden worden berekend. De meeste methoden die gebruikt worden om de waarde van π {\displaystyle \pi } $\pi$ te berekenen hebben wenselijke wiskundige eigenschappen. Ze zijn echter moeilijk te begrijpen zonder kennis van goniometrie en calculus. Sommige methoden zijn echter vrij eenvoudig, zoals deze vorm van de Gregory-Leibniz reeks:

π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ... {\displaystyle \pi ={{{frac {4}{1}}-{{frac {4}{3}+{{frac {4}{5}}-{frac {4}{7}}+{{frac {4}{9}}-{{frac {4}{11}}}. $\pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\,\ldots$

Hoewel deze reeks eenvoudig te schrijven en te berekenen is, is het niet eenvoudig om te zien waarom deze gelijk is aan π {{{em}. $\pi$ . Een veel eenvoudiger benadering is het tekenen van een denkbeeldige cirkel met straal r met het middelpunt op de oorsprong. Dan ligt elk punt ( x , y ) waarvan de afstand d $d$ tot de oorsprong kleiner is dan r , berekend volgens de stelling van Pythagoras, in de cirkel:

d = x 2 + y 2 {displaystyle d={x^{2}+y^{2}}}} $d={\sqrt {x^{2}+y^{2}}}$

Door een reeks punten binnen de cirkel te vinden, kan de oppervlakte A {\displaystyle A} $A$ van de cirkel worden geschat, bijvoorbeeld door gebruik te maken van gehele coördinaten voor een grote r {\displaystyle r} . Aangezien de oppervlakte A {\displaystyle A} $A$ van een cirkel gelijk is aan π {\displaystyle \pi } $\pi$ maal de straal in het kwadraat, kan π {\displaystyle \pi } $\pi$ worden benaderd met de volgende formule:

π = A r 2 {{frac {A}{r^{2}}}}}}. $\pi ={\frac {A}{r^{2}}}$

Oppervlakte, omtrek, diameter en straal van een cirkel berekenen

Gebied

Met behulp van de straal: A = π r 2 {Displaystyle A=pi r^{2}} $A=\pi r^{2}$

Met behulp van de diameter: A = π d 2 4 {Displaystyle A={{frac {{2}}{4}}} $A={\frac {\pi d^{2}}{4}}$

Met behulp van de omtrek: A = C 2 4 π {Displaystyle A={frac {C^{2}}{4\pi }} $A={\frac {C^{2}}{4\pi }}$

Omtrek

Met behulp van de diameter: C = π d {Displaystyle C=pi d} $C=\pi d$

Met behulp van de straal: C = 2 π r {Displaystyle C=2 π r} $C=2\pi r$

Met behulp van de oppervlakte: C = 2 π A {Displaystyle C=2{{sqrt {\pi A}}}. $C=2{\sqrt {\pi A}}$

Diameter

Gebruikmakend van zijn straal: d = 2 r {Displaystyle d=2r} $d=2r$

Met behulp van de omtrek: d = C π {Displaystyle d={Frac {C}{\pi }} $d={\frac {C}{\pi }}$

Met de oppervlakte: d = 2 A π {displaystyle d=2{sqrt {frac {A}{pi }}}} $d=2{\sqrt {\frac {A}{\pi }}}$

Straal

Met de diameter: r = d 2 {displaystyle r={{frac {d}{2}}}} $r={\frac {d}{2}}$

Met behulp van de omtrek: r = C 2 π {{{frac {C}{2\pi }}} $r={\frac {C}{2\pi }}$

Met behulp van de oppervlakte: r = A π {{ displaystyle r={frac {A}{pi }}}} $r={\sqrt {\frac {A}{\pi }}}$

Gerelateerde pagina's

Halve cirkel
Bol
De kwadratuur van de cirkel
Pi
Pi (letter)
Tau

Vragen en antwoorden

V: Wat is een cirkel?

A: Een cirkel is een ronde, tweedimensionale vorm. Alle punten op de rand van de cirkel liggen op dezelfde afstand van het middelpunt.

V: Wat gebruiken wiskundigen om de lengte van de straal van een cirkel weer te geven?

A: Wiskundigen gebruiken de letter r voor de lengte van de straal van een cirkel.

V: Wat wordt in cirkels geschreven als O?

A: Het middelpunt van een cirkel wordt vaak geschreven als O.

V: Hoe lang is de diameter van een cirkel?

A: De diameter (wat "helemaal" betekent) van een cirkel is een rechte lijn die van de ene kant naar de andere kant en dwars door het middelpunt van de cirkel gaat. Zij is gelijk aan tweemaal de straal (d is gelijk aan 2 maal r).

V: Welke letter gebruiken wiskundigen voor de omtrek?

A: Wiskundigen gebruiken C voor omtrek, wat "rondom" betekent.

V: Hoe kan men de oppervlakte binnen een cirkel berekenen?

A: De oppervlakte, A, binnen een cirkel kan worden berekend door de straal met zichzelf te vermenigvuldigen en vervolgens te vermenigvuldigen met ً (A is gelijk aan ً maal r maal r).