16-cel
In de vierdimensionale meetkunde is een 16-cel een regelmatig convex polychoron of polytoop in vier dimensies. Het is ook bekend als hexadecachoron. Het is een van de zes regelmatige convexe polychoren die voor het eerst zijn beschreven door de Zwitserse wiskundige Ludwig Schläfli in het midden van de 19e eeuw.
Conway noemt het een orthoplex voor orthant complex, evenals de hele klasse van kruispolytopen.
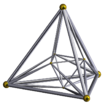
Een hexadecachoron
Geometrie
Het hexadecachoron is lid van de familie van polytopen die kruispolytopen worden genoemd en die in alle dimensies bestaan. Als zodanig is zijn dubbel polychoron de tesseract (de 4-dimensionale hyperkubus).
Het is begrensd door 16 cellen, allemaal regelmatige tetraëders. Het heeft 32 driehoekige vlakken, 24 ribben en 8 hoekpunten. De 24 ribben begrenzen 6 vierkanten in de 6 coördinatenvlakken.
De acht hoekpunten van het hexadecachoron zijn (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). Alle hoekpunten zijn verbonden door randen, behalve tegenovergestelde paren.
Het Schläfli symbool van het hexadecachoron is {3,3,4}. De hoekpuntfiguur is een regelmatige octaëder. Er zijn 8 tetraëders, 12 driehoeken en 6 ribben die elkaar op elk hoekpunt ontmoeten. De randfiguur is een vierkant. Er zijn 4 tetraëders en 4 driehoeken die elkaar bij elke rand ontmoeten.
Er is een lagere symmetrievorm van de 16-cel, een demitesseract of 4-demicube genoemd, een lid van de demihypercube familie, en voorgesteld door h{4,3,3}, en kan tweekleurig getekend worden met afwisselende tetraëdercellen.
Afbeeldingen
· 
Stereografische projectie
· 
Vier orthografische projecties
· 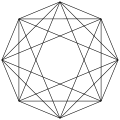
Een schuine orthogonale projectie binnen zijn regelmatige achthoekige Petrie veelhoek, die alle hoekpunten verbindt behalve de tegenoverliggende.
· 
De 16-cel heeft twee Wythoff-constructies, een regelmatige vorm en een afwisselende vorm, hier weergegeven als netten, waarbij de tweede wordt voorgesteld door afwisselend twee kleuren tetraëdercellen.
· 
Een 3D-projectie van een 16-cel die een dubbele rotatie uitvoert om twee orthogonale vlakken.
Vlakvullingen
Men kan de 4-dimensionale Euclidische ruimte vlakvullen met regelmatige 16-cellen. Dit heet de hexadecachorische honingraat en heeft het Schläfli symbool {3,3,4,3}. De dubbele vlakvulling, de icositetrachorische honingraat, {3,4,3,3}, bestaat uit regelmatige 24-cellen. Samen met de tesseractische honingraat {4,3,3,4} zijn dit de enige drie regelmatige vlakvullingen van R4 . Elke 16-cel heeft 16 buren waarmee hij een octaëder deelt, 24 buren waarmee hij alleen een rand deelt, en 72 buren waarmee hij alleen een enkel punt deelt. Vierentwintig 16-cellen ontmoeten elkaar op een gegeven hoekpunt in deze vlakvulling.
Projecties
De cel-eerste parallelle projectie van de 16-cel in de 3-ruimte heeft een kubusvormige omhulling. De dichtstbijzijnde en verste cellen worden geprojecteerd op ingeschreven tetraëders binnen de kubus, overeenkomend met de twee mogelijke manieren om een regelmatige tetraëder in een kubus in te schrijven. Rond elk van deze tetraëders bevinden zich 4 andere (niet-regelmatige) tetraëdervolumes die de beelden zijn van de 4 omringende tetraëdercellen, en de ruimte tussen de ingeschreven tetraëder en de kubus opvullen. De overige 6 cellen worden geprojecteerd op de vierkante vlakken van de kubus. In deze projectie van de 16-cel liggen alle randen op de zijvlakken van de kubus.
De cel-eerste perspectiefprojectie van de 16-cel in 3-ruimte heeft een triakis tetraëderomhullende. De indeling van de cellen binnen deze omhullende is analoog aan die van de cel-eerste parallelle projectie.
De punt-eerste parallelle projectie van de 16-cel in de 3-ruimte heeft een octaëdervormig omhulsel. Deze octaëder kan worden verdeeld in 8 tetraëderische volumes, door te snijden langs de coördinaatvlakken. Elk van deze volumes is het beeld van een paar cellen in de 16-cel. Het dichtstbijzijnde hoekpunt van de 16-cel bij de kijker projecteert op het centrum van de octaëder.
Tenslotte heeft de rand-eerste parallelle projectie een verkort octaëdervormig omhulsel, en de gezicht-eerste parallelle projectie een hexagonaal bipyramidaal omhulsel.
Gerelateerde pagina's
- 24-cel
- Polychoron
Zoek in de encyclopedie