Fourier reeksen
Joseph Fourier zei dat het mogelijk is om sinusgolven te gebruiken om een andere functie te benaderen. Dit is een reeks in wiskundige zin. Deze theorie kan worden veralgemeend tot de Fourier-transformatie. De wiskundige analyse van deze functies wordt Fourieranalyse genoemd.
In de 18e eeuw gebruikten wiskundigen als Euler, Lagrange en Bernoulli reeds sinusoïden om andere functies te benaderen en te modelleren. Toen Fourier in 1822 een werk over warmte publiceerde, zei hij dat dergelijke benaderingen bestaan voor elke dergelijke functie (die continu is in het interval). Aanvankelijk geloofde men hem niet, en het duurde bijna tien jaar voordat een bewijs (van een deel van het probleem) verscheen.
Tegenwoordig worden fourierreeksen veel gebruikt in de digitale signaalverwerking.
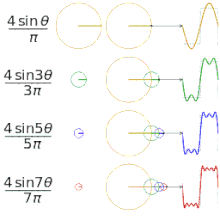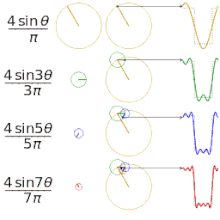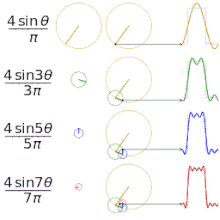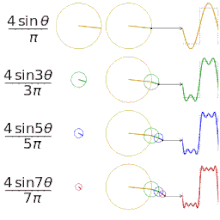
Het benaderen van verschillende "vierkante" functies met behulp van fourierreeksen
Vragen en antwoorden
V: Wie was Joseph Fourier?
A: Joseph Fourier was een Franse wiskundige die voorstelde dat sinusgolven gebruikt kunnen worden om een andere functie te benaderen.
V: Wat is een Fourier-reeks?
A: Een Fourierreeks is een reeks die sinusgolven gebruikt om een andere functie te benaderen.
V: Wat is de Fouriertransformatie?
A: De Fouriertransformatie is een veralgemening van de theorie die sinusgolven gebruikt om een andere functie te benaderen.
V: Wat is Fourieranalyse?
A: Fourieranalyse is een wiskundige analyse van de functies die sinusgolven gebruiken om een andere functie te benaderen.
V: Wie gebruikten in de 18e eeuw sinusoïdes om andere functies te benaderen en te modelleren?
A: Wiskundigen zoals Euler, Lagrange en Bernoulli gebruikten in de 18e eeuw sinusoïdes om andere functies te benaderen en te modelleren.
V: Wat stelde Fourier voor in zijn werk over warmte in 1822?
A: In zijn werk over warmte in 1822 stelde Fourier voor dat dergelijke benaderingen met sinusgolven bestaan voor elke continue functie in een gegeven interval.
V: Wat is het nut van Fourierreeksen in digitale signaalverwerking?
A: Fourierreeksen worden veel gebruikt in digitale signaalverwerking om signalen te benaderen en te analyseren.
