Fouriertransformatie | wiskundige functie die kan worden gebruikt om de basisfrequenties te vinden waaruit een golf bestaat

De Fouriertransformatie is een wiskundige functie die kan worden gebruikt om de basisfrequenties te vinden waaruit een golf bestaat. Stel u voor dat u een akkoord speelt op een piano. Bij het spelen mengen de geluiden van de noten van het akkoord zich en vormen een geluidsgolf. Dit werkt omdat de golven van de verschillende noten met elkaar interfereren door op verschillende punten in de golf bij elkaar op te tellen of uit te schakelen. Een Fourier-transformatie neemt deze complexe golf en is in staat de frequenties te vinden waaruit deze is opgebouwd, wat betekent dat de noten waaruit een akkoord is opgebouwd, kunnen worden gevonden.

De output van een Fouriertransformatie wordt soms een frequentiespectrum of -verdeling genoemd, omdat deze een verdeling van mogelijke frequenties van de input weergeeft. Deze functie kent vele toepassingen in cryptografie, oceanografie, machinaal leren, radiologie, kwantumfysica en geluidsontwerp en visualisatie.

De Fouriertransformatie van een functie f ( x ) f(x) , ook wel geschreven als F { f } }. {De Fouriertransformatie van een functie f ( x ) {F} wordt soms geschreven als F {f}. ${\mathcal {F}}\{f\}$ wordt gegeven door

F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x {displaystyle F(\alpha )={{{-}infty }^{+{{{{}infty }f(x)e^{-2pi i\alpha x},dx}. $F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}\,dx$

waar:

$\alpha$ is een frequentie.
F ( α ) {\displaystyle F(\alpha )} $F(\alpha )$ is de Fouriertransformatiefunctie en geeft een waarde die aangeeft hoe overheersend frequentie α {\alpha } $\alpha$ is in het originele signaal.
e - 2 π i α x {displaystyle e^{-2\pi i\alpha x}} $e^{-2\pi i\alpha x}$ staat voor het omwikkelen van de ingangsgolffunctie f ( x ) {displaystyle f(x)} rond de oorsprong van het complexe vlak bij een bepaalde frequentie α {displaystyle \alpha } . $\alpha$ .

De inverse Fouriertransformatie wordt gegeven door

f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {displaystyle f(x)={-{infty }^{+{infty }F(\alpha )e^{+2pi ix\alpha }, d\alpha }. $f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }\,d\alpha$

Een Fouriertransformatie laat zien welke frequenties zich in een signaal bevinden. Neem bijvoorbeeld een geluidsgolf die drie verschillende muzieknoten bevat: A, B en C. Een grafiek van de Fouriertransformatie van deze geluidsgolf (met de frequentie op de x-as en de intensiteit op de y-as) toont bij elke frequentie een piek die overeenkomt met een van de muzieknoten.

Veel signalen kunnen worden gecreëerd door cosinussen en sinussen met verschillende amplitudes en frequenties bij elkaar op te tellen. De Fouriertransformatie zet de amplitudes en fasen van deze cosinussen en sinussen uit tegen hun respectieve frequenties.

Fouriertransformaties zijn belangrijk, omdat veel signalen zinvoller zijn wanneer hun frequenties worden gescheiden. In het audiovoorbeeld hierboven is het niet duidelijk dat de tonen A, B en C in het signaal zitten als we het signaal bekijken ten opzichte van de tijd. Veel systemen doen verschillende dingen met verschillende frequenties, dus dit soort systemen kan worden beschreven aan de hand van wat ze met elke frequentie doen. Een voorbeeld hiervan is een filter dat hoge frequenties blokkeert.

De berekening van een Fouriertransformatie vereist inzicht in integratie en imaginaire getallen. Computers worden gewoonlijk gebruikt om Fouriertransformaties te berekenen van alles behalve de eenvoudigste signalen. De Fast Fourier Transform is een methode die computers gebruiken om snel een Fouriertransformatie te berekenen.

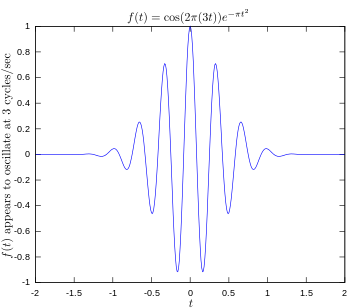
· Original function showing a signal oscillating at 3 hertz.

Originele functie die een signaal toont dat oscilleert op 3 hertz.

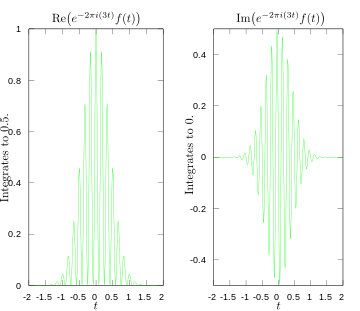
· Real and imaginary parts of integrand for Fourier transform at 3 hertz

Reële en imaginaire delen van de integrand voor Fouriertransformatie bij 3 hertz

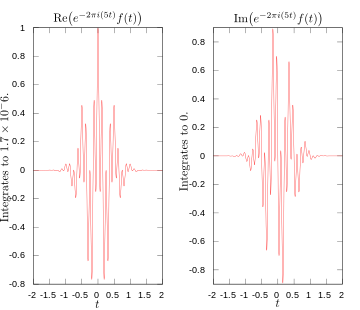
· Real and imaginary parts of integrand for Fourier transform at 5 hertz

Reële en imaginaire delen van de integrand voor Fouriertransformatie bij 5 hertz

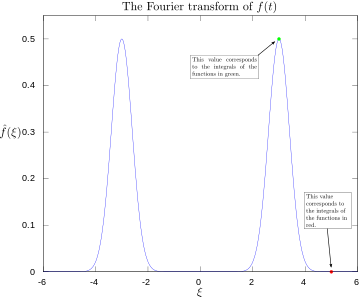
· Fourier transform with 3 and 5 hertz labeled.

Fouriertransformatie met 3 en 5 hertz gelabeld.

Gerelateerde pagina's

Fourieranalyse
Fourier-inversietheorie
Fourier-reeks
Laplace-transformatie

Vragen en antwoorden

V: Wat is de Fouriertransformatie?

A: De Fouriertransformatie is een wiskundige functie die kan worden gebruikt om de basisfrequenties te vinden waaruit een golf bestaat. Het neemt een complexe golf en vindt de frequenties waaruit deze is opgebouwd, zodat de noten waaruit een akkoord bestaat kunnen worden geïdentificeerd.

V: Wat zijn enkele toepassingen van de Fouriertransformatie?

A: De Fouriertransformatie kent vele toepassingen in cryptografie, oceanografie, machinaal leren, radiologie, kwantumfysica en geluidsontwerp en visualisatie.

V: Hoe wordt de Fouriertransformatie berekend?

A: De Fouriertransformatie van een functie f(x) wordt gegeven door F(ב) = ∫-∞+∞f(x)e-2נiבxdx waarbij ב een frequentie is. Dit levert een waarde op die aangeeft hoe overheersend frequentie ב is in het oorspronkelijke signaal. De inverse Fouriertransformatie wordt gegeven door f(x) = ∫-∞+∞F(ב)e+2נixבdב.

V: Hoe ziet een uitgang van een Fouriertransformatie eruit?

A: Een uitvoer van een Fourier Transformatie kan een frequentiespectrum of een verdeling worden genoemd, omdat deze een verdeling van mogelijke frequenties van de invoer weergeeft.

V: Hoe berekenen computers snelle Fourier Transformaties?

A: Computers gebruiken een algoritme genaamd Fast Fourier Transform (FFT) om snel alle transformaties van signalen te berekenen, behalve de eenvoudigste.

V: Wat laat het bekijken van signalen ten opzichte van de tijd ons niet zien?

A: Signalen bekijken ten opzichte van de tijd maakt niet duidelijk welke tonen erin voorkomen; veel signalen zijn zinvoller als hun frequenties worden gescheiden en afzonderlijk worden geanalyseerd.