Cross product

Belang van het kruisproduct

Omdat het een vectorbewerking is, is het kruisproduct uiterst belangrijk in allerlei wetenschappen (met name natuurkunde), techniek en wiskunde. Een belangrijk voorbeeld van het kruisproduct is het koppel of het moment. Een andere belangrijke toepassing is het magnetisch veld.

 

Visualiseren van het kruisproduct in drie dimensies

Het kruisproduct van a → en b → is een vector die we c → zullen noemen:

c → = a → × b → {Displaystyle {vec {c}}={{vec {a}}={{b}}}}

Dan wordt de grootte van c → gegeven door:

c = | c → | = | a → | b → | sin θ = a b sin θ {\displaystyle c=|{{\vec {c}}|=|{\vec {a}}|{\vec {b}}|{\sin \theta =absin \theta } ,

waarbij θ {\theta } de hoek is tussen a → {\displaystyle {\a}}} en b → {\displaystyle {\b}}} . De vector a → × b → staat loodrecht op zowel a → {\displaystyle {vec {a}}} als b → {\displaystyle {vec {b}}} . De richting van a → × b → wordt bepaald door een variatie op de rechterhandregel. Als je je rechterhand vasthoudt zoals in de figuur, staat je duim in de richting van c → {displaystyle {vec {c}}} De wijsvinger geeft de richting aan van a → en de tweede vinger wijst in de richting van b → . Als de hoek tussen uw wijsvinger en tweede vinger groter is dan 180°, moet u uw hand omdraaien.

 
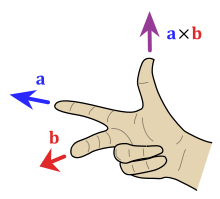
Het vinden van de richting van het kruisproduct.  

Hoe bereken je het kruisproduct in vectornotatie?

Zoals elke wiskundige bewerking kan het kruisproduct op een eenvoudige manier worden uitgevoerd.

Twee dimensies

Als
a → = ⟨ a 1 , a 2 ⟩ {displaystyle {a}}=hoek a_{1},a_{2} }
 en
b → = ⟨ b 1 , b 2 ⟩ {displaystyle {\vec {b}}}=kringloop b_{1},b_{2}}
 dan
a → × b → = ( a 1 b 2 - a 2 b 1 ) k ^ {displaystyle {vec {a}}=(a_{1}b_{2}-a_{2}b_{1}){hat {k}}}

 of

a → × b → = c → {\an5c}}
 en
c → = ⟨ 0 , 0 , a 1 b 2 - a 2 b 1 ⟩ = ( a 1 b 2 - a 2 b 1 ) k ^ {displaystyle {vec {c}}=hoek 0,0,a_{1}b_{2}-a_{2}b_{1}hoek =(a_{1}b_{2}-a_{2}b_{1}}}}}

k ^ {k}} is gewoon een symbool dat zegt dat onze nieuwe vector omhoog wijst (in de z-richting). Als je twee vectoren die allebei in het x-y-vlak liggen "kruist", zal het product altijd loodrecht staan op beide vectoren, en als beide vectoren in het x-y-vlak liggen, is de enige manier om loodrecht op beide te staan de z-richting. Indien de waarde van a 1 b 2 - a 2 b 1 {{1}b_{2}-a_{2}b_{1}} positief is, dan wijst het naar buiten; indien de waarde negatief is, dan wijst het naar binnen.

Drie dimensies

Als
a → = ⟨ a 1 , a 2 , a 3 ⟩ {displaystyle {a}}=hoek a_{1},a_{2},a_{3}}
 en
b → = ⟨ b 1 , b 2 , b 3 ⟩ {\displaystyle {\vec {b}}=\langle b_{1},b_{2},b_{3}\rangle }
 dan
a → × b → = ⟨ a 2 b 3 - a 3 b 2 , a 3 b 1 - a 1 b 3 , a 1 b 2 - a 2 b 1 ⟩ {\displaystyle {a}}}==leek a_{2}b_{3}-a_{3}b_{2},a_{3}b_{1}-a_{1}b_{3},a_{1}b_{2}-a_{2}b_{1}}.

 

Basiseigenschappen van het kruisproduct

a → × b → = - b → × a → {Displaystyle {a}}=-{{vec {b}}=-{{vec {b}}}.

a → × ( b → + c → ) = a → × b → + a → × c → {\displaystyle {\a}}{\avec {a}}{\avec {b}}+{\a}}} ={\avec {a}}{\avec {b}}+{\a}}{\avec {c}}}}}

c ( a → × b → ) = ( c a → ) × b → = a → × ( c b → ) {\displaystyle c({a}})=(c{vec {a}})¦(c{vec {a}})¦(c{vec {b}})}.