Vector (wiskunde) | wiskundig object

A vector

Een vector is een wiskundig object met een grootte, magnitude genaamd, en een richting. Het wordt vaak weergegeven met vetgedrukte letters (zoals u {mathbf {u}}. } $\mathbf {u}$ , v {mathbf {v} } $\mathbf {v}$ , w {w}. } $\mathbf {w}$ ), of als een lijnstuk van het ene punt naar het andere (zoals in A B → ${\overrightarrow {AB}}$ ).

Een vector wordt bijvoorbeeld gebruikt om de afstand en de richting aan te geven waarin iets beweegt. Als men de weg vraagt, en men zegt "Loop een kilometer naar het noorden", dan is dat een vector, maar als men zegt "Loop een kilometer", zonder een richting aan te geven, dan is dat een scalair.

Wij tekenen vectoren meestal als pijlen. De lengte van de pijl is evenredig met de grootte van de vector. De richting waarin de pijl wijst, is de richting van de vector.

Voorbeelden van vectoren

John loopt 20 meter naar het noorden. De richting "noord" samen met de afstand "20 meter" is een vector.
Een appel valt naar beneden met een snelheid van 10 meter per seconde. De richting "naar beneden" in combinatie met de snelheid "10 meter per seconde" is een vector. Dit soort vector wordt ook wel snelheid genoemd.

Voorbeelden van scalars

De afstand tussen twee plaatsen is 10 kilometer. Deze afstand is geen vector, want hij bevat geen richting.
Het aantal vruchten in een doos is geen vector.
Een persoon die wijst is geen vector, want er is alleen een richting. Er is geen magnitude (bijvoorbeeld de afstand van de vinger van de persoon tot een gebouw).
De lengte van een object.
Een auto rijdt met 100 kilometer per uur. Dit beschrijft geen vector, want er is alleen een magnitude, maar geen richting.

Meer voorbeelden van vectoren

Verplaatsing is een vector. Verplaatsing is de afstand die iets in een bepaalde richting aflegt. Een maat voor afstand alleen is een scalair.
Een kracht met richting is een vector.
Snelheid is een vector, want het is een snelheid in een bepaalde richting.
Versnelling is de snelheid waarmee de snelheid verandert. Een voorwerp versnelt als het van snelheid of richting verandert.

Hoe vectoren toevoegen

Vectoren toevoegen op papier met de kop-staartmethode

De kop-staartmethode van het optellen van vectoren is handig om op papier een schatting te maken van het resultaat van het optellen van twee vectoren. Om het te doen:

Elke vector wordt getekend als een pijl met een lengte erachter, waarbij elke lengte-eenheid op het papier een bepaalde grootte van de vector voorstelt.
Teken de volgende vector, met de staart (einde) van de tweede vector aan de kop (voorzijde) van de eerste vector.
Herhaal dit voor alle volgende vectoren: Teken de staart van de volgende vector aan de kop van de vorige.
Trek een lijn van de staart van de eerste vector naar de kop van de laatste vector - dat is de resultante (som) van alle vectoren.

Dit wordt de "Head to Tail"-methode genoemd, omdat elke kop van de vorige vector leidt tot de staart van de volgende.

Gebruik van het componentformulier

^{[moet worden uitgelegd ]}

De componentvorm gebruiken om twee vectoren op te tellen betekent letterlijk de componenten van de vectoren optellen om een nieuwe vector te maken. Laat bijvoorbeeld a en b twee tweedimensionale vectoren zijn. Deze vectoren kunnen worden geschreven in termen van hun componenten.

a = ( a x , a y ) {displaystyle \mathbf {a} =(a_{x},a_{y})} $\mathbf {a} =(a_{x},a_{y})$

b = ( b x , b y ) {displaystyle \mathbf {b} =(b_{x},b_{y})} $\mathbf {b} =(b_{x},b_{y})$

Stel dat c de som is van deze twee vectoren, zodat c = a + b. Dit betekent dat c = ( a x + b x , a y + b y ) {{displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} $\mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})$ .

Hier volgt een voorbeeld van optelling van twee vectoren met behulp van hun componentvormen:

a = ( 3 , - 1 ) {displaystyle \mathbf {a} =(3,-1)}. $\mathbf {a} =(3,-1)$

b = ( 2 , 2 ) {displaystyle \mathbf {b} =(2,2)}. $\mathbf {b} =(2,2)$

c = a + b = ( a x + b x , a y + b y ) = ( 3 + 2 , - 1 + 2 ) = ( 5 , 1 ) {\displaystyle {\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}} ${\begin{aligned}\mathbf {c} &=\mathbf {a} +\mathbf {b} \\&=(a_{x}+b_{x},a_{y}+b_{y})\\&=(3+2,-1+2)\\&=(5,1)\end{aligned}}$

Deze methode werkt voor alle vectoren, niet alleen voor tweedimensionale.

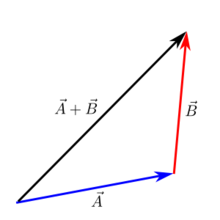
Kop-staart toevoeging

Hoe vectoren vermenigvuldigen

Gebruik van het scalair product

Het scalair product is een methode om vectoren te vermenigvuldigen. Het levert een scalair op. Het gebruikt de componentvorm:

a = ( 2 , 3 ) b = ( 1 , 4 ) a ⋅ b = ( 2 , 3 ) ⋅ ( 1 , 4 ) = ( 2 ⋅ 1 ) + ( 3 ⋅ ${\begin{aligned}\mathbf {a} &=(2,3)\\\mathbf {b} &=(1,4)\\\mathbf {a} \cdot \mathbf {b} &=(2,3)\cdot (1,4)\\&=(2\cdot 1)+(3\cdot 4)\\&=2+12\\&=14\end{aligned}}$

Gebruik van het kruisproduct

Het kruisproduct is een andere methode om vectoren te vermenigvuldigen. In tegenstelling tot het puntproduct levert het een vector op. Gebruik de componentvorm:

a × b = | a | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} |mathbf {b} |heta> \mathbf {n}. } $\mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n}$

Hier betekent | a | {\displaystyle |mathbf {a} | $|\mathbf {a} |$ betekent de lengte van een {displaystyle \mathbf {a} } $\mathbf {a}$ en n is de eenheidsvector op . $\mathbf {n}$ is de eenheidsvector die loodrecht staat op zowel a {displaystyle \mathbf {a}} $\mathbf {a}$ en b. } $\mathbf {b}$ .

Vermenigvuldigen met een scalair

Om een vector te vermenigvuldigen met een scalair (een gewoon getal), vermenigvuldigt u het getal met elke component van de vector:

c x = ( c x 1 , c x 2 , . . . , c x n ) {displaystyle c,athbf {x} =(c,x_{1},c,x_{2},...,c,x_{n})} $c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})$

Een voorbeeld hiervan is

c = 5 x = ( 3 , 4 ) c x = ( 5 ⋅ 3 , 5 ⋅ ⋅ 4)¿d&=(15,20)¿end{aligned}}}. ${\begin{aligned}c&=5\\\mathbf {x} &=(3,4)\\c\,\mathbf {x} &=(5\cdot 3,5\cdot 4)\\&=(15,20)\end{aligned}}$

Gerelateerde pagina's

Analytische meetkunde
Nietige vector
Eenheidsvector
Vectorveld
Vectorafbeeldingen
Vectorruimte
Vectorsubruimte

Vragen en antwoorden

V: Wat is een vector?

A: Een vector is een wiskundig object met een grootte, magnitude genaamd, en een richting. Hij wordt vaak weergegeven met vette letters of als een lijnstuk van het ene punt naar het andere.

V: Hoe tekenen wij vectoren meestal?

A: Wij tekenen vectoren gewoonlijk als pijlen. De lengte van de pijl is evenredig met de grootte van de vector en de richting waarin de pijl wijst is de richting van de vector.

V: Wat betekent het als iemand de weg vraagt?

A: Als iemand de weg vraagt, en hij zegt "Loop een kilometer naar het noorden", dan is dat een vector, maar als hij zegt "Loop een kilometer", zonder een richting aan te geven, dan is dat een scalair.

V: Wat zijn enkele voorbeelden van hoe vectoren kunnen worden gebruikt?

A: Vectoren kunnen worden gebruikt om de afstand en de richting van een beweging aan te geven. Ze kunnen ook worden gebruikt om de weg te vragen of om door een gebied te navigeren.

V: Hoe worden vectoren wiskundig voorgesteld?

A: Vectoren worden vaak weergegeven met vetgedrukte letters (zoals u, v, w) of als een lijnstuk van het ene punt naar het andere (zoals in A→B).

V: Wat betekent het als iets scalair wordt genoemd?

A: Wanneer iets als scalair wordt aangeduid, betekent dit dat er geen richtingsinformatie aan gekoppeld is; alleen numerieke waarden zoals afstand of snelheid.