AlegsaOnline.com

Magnetisch veld

Schrijver: Leandro Alegsa

17-12-2020

Het magnetisch veld is het gebied rond een magneet waarin zich een magnetische kracht bevindt. Bewegende elektrische ladingen kunnen magnetische velden maken. Magnetische velden zijn meestal te zien aan magnetische fluxlijnen. De richting van het magnetisch veld is te allen tijde te zien aan de richting van de magnetische fluxlijnen. De sterkte van een magneet heeft te maken met de ruimtes tussen de magnetische fluxlijnen. Hoe dichter de fluxlijnen bij elkaar liggen, hoe sterker de magneet is. Hoe verder weg ze zijn, hoe zwakker. De fluxlijnen zijn te zien door ijzervijlsel over een magneet te leggen. Het ijzervijlsel beweegt en schikt zich in de lijnen. Magnetische velden geven kracht aan andere deeltjes die het magnetisch veld raken.

In de fysica is het magnetisch veld een veld dat door de ruimte gaat en dat een magnetische kracht elektrische ladingen en magnetische dipolen doet bewegen. Magnetische velden bevinden zich rond elektrische stromen, magnetische dipolen en veranderende elektrische velden.

Wanneer ze in een magnetisch veld worden geplaatst, staan de magnetische dipolen in één lijn met hun assen parallel aan de veldlijnen, zoals te zien is wanneer ijzervijlsel in de aanwezigheid van een magneet aanwezig is. Magnetische velden hebben ook hun eigen energie en momentum, met een energiedichtheid die evenredig is met het kwadraat van de veldsterkte. Het magnetisch veld wordt gemeten in de eenheden van teslas (SI-eenheden) of gauss (cgs-eenheden).

Er zijn enkele opmerkelijke soorten magnetisch veld. Voor de fysica van magnetische materialen, zie magnetisme en magneet, en meer specifiek diamagnetisme. Voor magnetische velden gemaakt door het veranderen van elektrische velden, zie elektromagnetisme.

Het elektrisch veld en het magnetisch veld zijn componenten van het elektromagnetisch veld.

De wet van het elektromagnetisme is opgericht door Michael Faraday.

H-veld

Natuurkundigen kunnen zeggen dat de kracht en de koppels tussen twee magneten worden veroorzaakt door magnetische polen die elkaar afstoten of aantrekken. Dit is als de Coulomb-kracht die dezelfde elektrische ladingen afstoot of tegengestelde elektrische ladingen aantrekt. In dit model wordt een magnetisch H-veld geproduceerd door magnetische ladingen die rond elke pool worden 'gesmeerd'. Het H-veld is dus als het elektrische veld E dat begint bij een positieve elektrische lading en eindigt bij een negatieve elektrische lading. Bij de noordpool wijzen alle H-veldlijnen weg van de noordpool (binnen of buiten de magneet) terwijl bij de zuidpool (binnen of buiten de magneet) alle H-veldlijnen naar de zuidpool wijzen. Een noordpool voelt dan een kracht in de richting van het H-veld terwijl de kracht op de zuidpool tegengesteld is aan het H-veld.

In het magnetische poolmodel wordt de elementaire magnetische dipool m gevormd door twee tegenover elkaar liggende magnetische polen met poolsterkte qm, gescheiden door een zeer kleine afstand d, zodat m = qm d.

Helaas kunnen magnetische polen niet los van elkaar bestaan. Alle magneten hebben noord-zuidparen die niet gescheiden kunnen worden zonder dat er twee magneten met elk een noord-zuidpaar ontstaan. Ook zijn magnetische polen niet verantwoordelijk voor magnetisme dat wordt veroorzaakt door elektrische stromen, noch voor de kracht die een magnetisch veld uitoefent op bewegende elektrische ladingen.

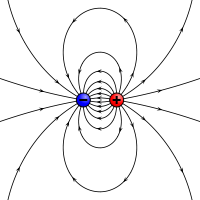
Het magnetische poolmodel : twee tegengestelde polen, Noord (+) en Zuid (-), gescheiden door een afstand d produceren een H-veld (lijnen).

H-veld en magnetische materialen

Het $H-veld$ wordt gedefinieerd als:

H ≡ B μ 0 - M , {\\\\\\\\\\\\\\\\f {H} \ Ik wil dat je het weet, maar ik wil niet dat je het weet. Mattebf... $\mathbf {H} \ \equiv \ {\frac {\mathbf {B} }{\mu _{0}}}-\mathbf {M} ,$ (definitie van $H$ in SI-eenheden)

Met deze definitie wordt Ampère's wet:

∮ H ⋅ d ℓ = ∮ ( B μ 0 - M ) ⋅ d ℓ = I t to t - I b = I f {\\\\\\\\\\tbf {H} \Ik heb het niet over dboldsymbol, maar over links... }I_I_Mathrm {\mathrm} }=I_I_mathrm {\mathrm {f} }} $\oint \mathbf {H} \cdot d{\boldsymbol {\ell }}=\oint \left({\frac {\mathbf {B} }{\mu _{0}}}-\mathbf {M} \right)\cdot d{\boldsymbol {\ell }}=I_{\mathrm {tot} }-I_{\mathrm {b} }=I_{\mathrm {f} }$

waarbij $If$ de 'vrije stroom' vertegenwoordigt die door de lus wordt ingesloten, zodat de lijnintegraal van $H in het$ geheel niet afhankelijk is van de gebonden stromen. Voor het differentiaal equivalent van deze vergelijking zie Maxwell's vergelijkingen. De wet van Ampère leidt tot de randvoorwaarde:

H 1 , ∥ - H 2 , ∥ = K f , H_1,\parallel }H_2,\parallel }=mathbf {\text{f},} $H_{1,\parallel }-H_{2,\parallel }=\mathbf {K} _{\text{f}},$

waarbij $Kf$ de oppervlakte vrije stroomdichtheid is.

Op dezelfde manier is een oppervlakte-integraal van $H$ over een gesloten oppervlak onafhankelijk van de vrije stromen en kiest het de 'magnetische ladingen' binnen dat gesloten oppervlak uit:

∮ S μ 0 H ⋅ d A = ∮ S ( B - μ 0 M ) ⋅ d A = ( 0 - ( - q M ) ) = q M , {\\\\mu _{0}mathbf {H} \Ik heb geen idee wat er aan de hand is. \Mathbf =oint... \mathbf {A} =(0-(-q_{M}))=q_{M},} $\oint _{S}\mu _{0}\mathbf {H} \cdot \mathrm {d} \mathbf {A} =\oint _{S}(\mathbf {B} -\mu _{0}\mathbf {M} )\cdot \mathrm {d} \mathbf {A} =(0-(-q_{M}))=q_{M},$

die niet afhankelijk is van de vrije stromen.

Het $H-veld$ kan dus worden opgesplitst in twee onafhankelijke delen:

H = H 0 + H d , {\\\\\\\\\\\\\\\\\f {H}=mathbf {H} =mathbf {H} ...+mathbf... _{d},\,} $\mathbf {H} =\mathbf {H} _{0}+\mathbf {H} _{d},\,$

waarbij $H0$ het toegepaste magnetische veld is door de vrije stromen en $Hd$ het demagnetiserende veld door de gebonden stromen.

Het magnetische $H-veld$ refactoren dus de gebonden stroom in termen van 'magnetische ladingen'. De H-veldlijnen lopen alleen rond 'vrije stroom' en beginnen en eindigen, in tegenstelling tot het magnetische B-veld, ook bij de magnetische polen.

Gerelateerde pagina's

Vragen en antwoorden

V: Wat is een magnetisch veld?

A: Een magnetisch veld is het gebied rond een magneet waar een magnetische kracht heerst door de werking van bewegende elektrische ladingen.

V: Hoe kan de sterkte van een magneet worden bepaald?

A: De sterkte van een magneet kan worden bepaald door te kijken naar de afstand tussen de magnetische lijnen - hoe dichter bij elkaar, hoe sterker de magneet.

V: Wat gebeurt er als deeltjes een magnetisch veld raken?

Antwoord: Wanneer de deeltjes het magnetische veld raken, krijgen ze er kracht van.

V: Wat betekent het dat iets zijn eigen energie en dynamiek heeft?

Antwoord: Eigen energie en momentum hebben betekent dat iets zijn eigen eigenschappen heeft waardoor het onafhankelijk van andere voorwerpen of krachten kan bewegen of handelen.

V: Hoe meet u de sterkte van een magnetisch veld?

A: De magnetische veldsterkte wordt gemeten in teslax (SI-eenheden) of gauss (cgs-eenheden).

V: Wie heeft de wet van het elektromagnetisme opgesteld?

Antwoord: Michael Faraday stelde de wet van het elektromagnetisme vast.

V: Wat gebeurt er als ijzervlokken in de buurt van een magneet worden geplaatst?

Antwoord: Wanneer ijzervlokken in de buurt van een magneet worden geplaatst, bewegen ze en rangschikken ze zich in fluxlijnen die de richting en sterkte van het magnetische veld aangeven.