AlegsaOnline.com

Fractaal: definitie, voorbeelden en praktische toepassingen

Ontdek wat een fractaal is, bekijk voorbeelden (Mandelbrot, takken) en leer praktische toepassingen in wetenschap, technologie en kunst.

Schrijver: Leandro Alegsa Aanmaakdatum: 20 april 2021 Laatste update: 21 februari 2026

simple.wikipedia.org · CC0

Een fractal is een patroon dat, wanneer het als een afbeelding wordt gezien, een beeld oplevert dat, wanneer erop wordt ingezoomd, nog steeds hetzelfde beeld oplevert. Het kan in delen worden geknipt die eruit zien als een kleinere versie van het plaatje waarmee werd begonnen. Het woord fractal werd in 1975 door Benoît Mandelbrot gemaakt van het Latijnse woord fractus, dat "gebroken" of "gebroken" betekent. Een eenvoudig voorbeeld is een boom die zich vertakt in kleinere takken, en die takken weer in kleinere takken enzovoort. Fractals zijn niet alleen mooi, maar hebben ook veel praktische toepassingen.

Wat kenmerkt een fractal?

Zelfgelijkheid (self-similarity): delen van het patroon lijken sterk op het geheel, bij verschillende schaalniveaus. Dit kan precies gelijk zijn (strikte zelfgelijkheid) of alleen in statistische zin (statistische zelfgelijkheid).
Schaalonafhankelijkheid: het patroon toont vergelijkbare structuren of regels ongeacht de vergrotingsfactor.
Complexiteit uit eenvoudige regels: veel fractals ontstaan door herhaalde, eenvoudige bewerkingen (iteratie) toe te passen.
Fractale dimensie: in tegenstelling tot gewone meetkundige objecten hebben fractals vaak een niet-gehele (niet-integer) dimensie — een maat voor hoe volledig ze de ruimte opvullen. Deze fractale dimensie geeft een preciezere beschrijving dan alleen 'lijn', 'vlak' of 'volume'.

Voorbeelden (natuur en wiskunde)

Natuurlijke voorbeelden: bomen en hun takken, varens (zoals de kromming in sommige varenbladeren), de structuur van longen en bloedvaten, kustlijnen, sneeuwvlokken en bliksemschichten. Deze structuren tonen vaak herhaling op verschillende schalen.
Wiskundige fractals: de Mandelbrot- en Julia-verzamelingen (bekend uit fractalkunst en -onderzoek), de Cantor-set, de Koch-sneeuwvlok en de Sierpinski-driehoek. Deze worden gevormd door eenvoudige herhaalde regels en laten perfecte of bijna-perfecte zelfgelijkheid zien.

Wat is fractale dimensie? (kort)

De fractale dimensie is een manier om te meten hoe 'gevuld' een fractal object is. Een veelgebruikte methode is de box-counting-dimensie: tel hoeveel vakjes N(ε) van grootte ε nodig zijn om het object te dekken. De fractale dimensie D wordt dan benaderd door:

D ≈ (log N(ε)) / (log (1/ε)) voor kleine ε.

Bij klassieke lijnen, vlakken en volumes levert dit respectievelijk D ≈ 1, 2 en 3 op; fractals hebben vaak een fractale dimensie die tussen die getallen ligt (bijv. 1,26 of 1,89), wat aangeeft dat ze ingewikkelder zijn dan een lijn maar niet helemaal een vlak opvullen.

Praktische toepassingen van fractals

Computergraphics en animatie: fractals worden gebruikt om realistische landschappen, wolken, bomen en texturen te genereren met relatief eenvoudige regels (procedural generation).
Telecommunicatie: fractale antennes gebruiken zichzelf-herhalende geometrieën om op meerdere frequenties goed te kunnen werken in compact formaat.
Data- en beeldcompressie: fractale-compressie benut herhalende patronen binnen beelden om opslag kleiner te maken (hoewel andere methoden tegenwoordig vaker gebruikt worden).
Geologie en geografie: modellering van kustlijnen, riviernetwerken en aardbevingsstatistieken maakt gebruik van fractale principes om schaalonafhankelijke eigenschappen te beschrijven.
Biologie en geneeskunde: structuren zoals longblaasjes, bloedvaten en neurale netwerken hebben fractalachtige eigenschappen; inzicht daarin helpt bij modelleren van groei en diagnose.
Signaalverwerking en financiële analyse: schalingseigenschappen en lange-termijn afhankelijke patronen in tijdreeksen (bijv. financiële data) worden soms met fractale technieken bestudeerd.
Kunst en design: fractals inspireren visuele kunst, architectuur en patroonontwerp door hun complexe maar coherente schoonheid.

Eenvoudig zelf een fractal maken (voorbeeld: Sierpinski-driehoek, chaos game)

Teken een grote driehoek op papier en markeer de drie hoekpunten A, B en C.
Kies een willekeurig startpunt binnen de driehoek.
Herhaal veel keer: kies willekeurig één van de drie hoekpunten en zet een punt halverwege tussen het huidige punt en dat hoekpunt. Gebruik dat nieuwe punt als huidige punt.
Na veel iteraties verschijnt langzaam de Sierpinski-driehoek — een duidelijk fractaal patroon.

Samenvatting

Fractals verbinden wiskundige regels met natuurlijke vormen: eenvoudige, herhaalde processen leiden tot ingewikkelde, schaalonafhankelijke structuren. Ze zijn zowel esthetisch aantrekkelijk als praktisch bruikbaar in wetenschap, techniek en kunst. Of je nu een programmeur bent die realistische werelden wil genereren of een natuuronderzoeker die patronen in de werkelijkheid bestudeert, fractals bieden krachtige inzichten en toepassingen.

Een Sierpinski driehoek, na 7 iteraties.

De Mandelbrotverzameling is een beroemd voorbeeld van een fractal.

Voorbeelden

Er zijn vele soorten fractals, op zeer uiteenlopende manieren gemaakt. Een voorbeeld is de Sierpinski-driehoek, waar binnen de grote driehoek een oneindig aantal kleine driehoekjes ligt. Een ander voorbeeld is de Mandelbrotverzameling, genoemd naar Benoît Mandelbrot. De Sierpinksi-driehoek is opgebouwd uit patronen, maar de Mandelbrot-verzameling is gebaseerd op een vergelijking.

Er zijn ook veel natuurlijke voorbeelden van fractals in de natuur, zoals bomen, sneeuwvlokken, sommige groenten en kustlijnen.

De Koch Curve

De Koch Curve is een eenvoudig voorbeeld van een fractal. Begin eerst met een deel van een rechte lijn - een rechte lijnstuk genoemd. Snijd de lijn in 3 stukken van dezelfde grootte. Haal het midden van die stukken weg, en zet er het bovenste deel van een driehoek in met zijden die even lang zijn als het weg te snijden stuk. We hebben nu 4 lijnstukken die elkaar aan de uiteinden raken. We kunnen nu wat we net deden met het eerste lijnstuk doen met elk van de 4 stukjes. We kunnen nu hetzelfde steeds opnieuw doen met alle bits die we hebben. We doen dit nu voor eeuwig en kijken wat we uiteindelijk hebben.

De lengte van de Koch Curve is oneindig, en de oppervlakte van de Koch Curve is nul. Dit is heel vreemd. Een lijnstuk (met dimensie 1) kan een lengte hebben van 1, maar het heeft een oppervlakte van 0. Een vierkant van lengte 1 en breedte 1 (met dimensie 2) zal oppervlakte 1 hebben en lengte oneindig.

Gelijkenis dimensie

De Koch Curve lijkt dus groter te zijn dan iets van dimensie 1, en kleiner dan iets van dimensie 2. Het idee van de similariteitsdimensie is om een dimensie te geven die een beter idee geeft van lengte of oppervlakte voor fractals. Dus, voor een Koch Curve, willen we een dimensie tussen 1 en 2.

De Koch Curve kan in vier stukken worden geknipt, die elk 1 3 {\displaystyle {{1}{3}} ${\frac {1}{3}}$ van de grootte van het origineel zijn. Het aantal stukken waarin een fractal kan worden geknipt noemen we N {\displaystyle N} $N$ , en het verschil in grootte noemen we B {\displaystyle B} $B$ . Die plaatsen we in de vergelijking:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}} ${\frac {\log N}{-\log B}}$

Waarbij log {\log} $\log$ de logaritme van een getal is. Dit getal is de Hausdorff dimensie van de fractal. In de Koch Curve, is dit log 4 - log 1 3 = 1.2619... {\displaystyle {\frac {\log 4}{-log {\frac {1}{3}}}}=1.2619... ${\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619...$ zoals we wilden.

De Koch Curve is een van de eenvoudigste fractal vormen, en zijn dimensie is dus gemakkelijk te berekenen. De similariteitsdimensie en de Hausdorff-dimensie zijn beide gelijk. Dit geldt niet voor meer complexe fractals.

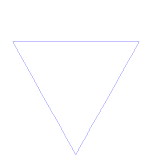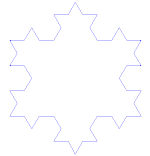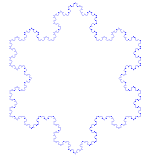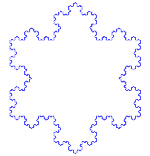
Koch sneeuwvlok

De Koch sneeuwvlok (of Koch ster) is hetzelfde als de Koch kromme, behalve dat het begint met een gelijkzijdige driehoek in plaats van een lijnstuk.

Gebruikt

Fractals hebben vele toepassingen, bijvoorbeeld in de biologie (longen, nieren, hartslagvariabiliteit, enz...), bij aardbevingen, in de financiële wereld waar zij verband houden met de zogenaamde zware staartdistributies en in de natuurkunde. Dit wijst erop dat fractals bestudeerd moeten worden om te begrijpen waarom fractals zo vaak voorkomen in de natuur.

Sommige fractals bestaan alleen om artistieke redenen, maar andere zijn zeer nuttig. Fractals zijn zeer efficiënte vormen voor radioantennes en worden gebruikt in computerchips om alle componenten efficiënt met elkaar te verbinden. Ook kustlijnen kunnen worden beschouwd als fractals.

Vragen en antwoorden

V: Wat is een fractal?

A: Een fractal is een patroon dat, gezien als een afbeelding, een beeld oplevert dat nog steeds hetzelfde beeld oplevert als je erop inzoomt.

V: Wie heeft de term "fractal" bedacht?

A: Benoît Mandelbrot heeft in 1975 de term "fractal" bedacht.

V: Wat is de etymologie van het woord "fractal"?

A: Het woord "fractal" is afgeleid van het Latijnse woord "fractus", wat "gebroken" of "gebroken" betekent.

V: Kunnen fractals in stukken worden geknipt?

A: Ja, fractals kunnen in delen worden geknipt die eruit zien als een kleinere versie van de afbeelding waarmee ze begonnen.

V: Kunt u een voorbeeld geven van een fractal?

A: Een eenvoudig voorbeeld van een fractal is een boom die zich vertakt in kleinere takken, en die weer in kleinere takken enzovoort.

V: Welke praktische toepassingen hebben fractals?

A: Fractals hebben veel praktische toepassingen, zoals in computerafbeeldingen, geneeskunde, natuurkunde en financiën.

V: Waarom zijn fractals belangrijk?

A: Fractals zijn belangrijk omdat ze ons kunnen helpen om complexe natuurverschijnselen te begrijpen en om nauwkeurigere modellen en simulaties te maken.