Lichtklok

De lichtklok is een eenvoudige manier om een basiskenmerk van Bijzondere relativiteit te laten zien. Een klok is ontworpen om te werken door een lichtflits van een verre spiegel te laten weerkaatsen en door zijn terugkeer te gebruiken om een andere lichtflits te activeren, terwijl hij tegelijkertijd telt hoeveel flitsen er onderweg zijn opgetreden. Het is gemakkelijk om te laten zien dat mensen op aarde die een ruimteschip zien vliegen met zo'n klok, het relatief langzaam zien tikken. Dit effect wordt tijddilatatie genoemd.

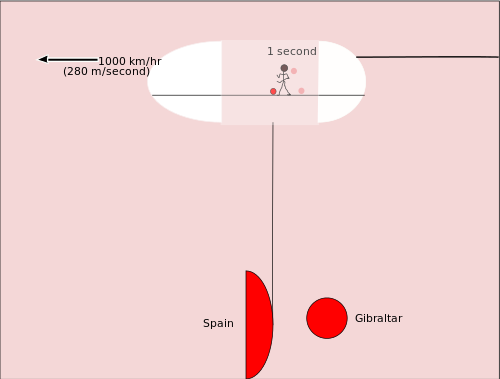
Voordat we de lichtklok bestuderen, moeten we een ander soort relativiteit overwegen. Stel je voor dat iemand een basketbal in het ruim van een grote vrachtvliegtuig aan het dribbelen is. De basketbalspeler beweegt zich in dezelfde richting als het straalvliegtuig. De andere mensen in het vliegtuig zien hem een meter of twee bewegen terwijl hij één keer dribbelt. Tussen het moment dat de bal de eerste keer stuitert en het moment dat de bal de tweede keer stuitert, is ongeveer een seconde verstreken. Maar toen de eerste stuitering plaatsvond was de basketbal over Gibraltar, en toen de tweede stuitering plaatsvond was de basketbal over het water dichter bij Spanje. Dus het basketbal heeft 280 meter verplaatst met betrekking tot de aarde.

Overweeg nu een enigszins vergelijkbare kwestie van relatieve beweging. Deze keer gaan we nadenken over wat mensen die naar sterren kijken vanaf de Noordpool zien als er een heel snel ruimteschip overheen vliegt. We kunnen de algebra en de stelling van Pythagoras gebruiken om uit te rekenen hoeveel tijd er op het ruimteschip vertraagt. Het enige andere dat we nodig hebben is de vergelijking die afstand, d, snelheid of snelheid van de reis, r, en tijd, t met elkaar in verband brengt:

d = rt

De snelheid van het licht is constant, dus we zullen deze waarde toepassen op twee problemen. We zullen de snelheid van het licht c noemen, omdat dit de letter is die wetenschappers meestal gebruiken om het te benoemen.

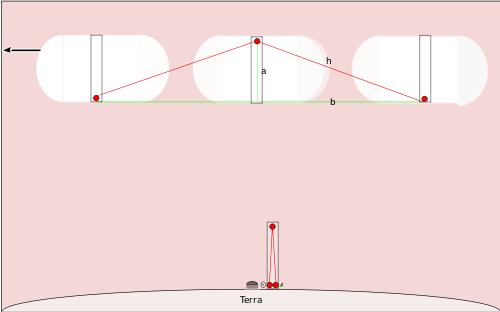
Een klok wordt gemaakt door een lichtopbrengst aan de onderkant van een lange paal, een spiegel boven op de paal en een elektronische lichtdetector onderaan de paal. De klok wordt gestart door een schakelaar kort te sluiten die een lichtflits van de onderkant van de paal naar de bovenkant van de paal stuurt, waar het wordt teruggekaatst naar de onderkant van de paal. Wanneer de lichtdetector onderaan de paal het knipperen van het licht ziet, doet hij twee dingen. Hij voegt er één toe aan de teller die er aan vastzit, en hij vuurt nog een lichtflits af tot aan de spiegel. Als die lichtknippering weer op de bodem komt, verandert het aantal in twee en gaat er weer een lichtknippering af. Omdat het licht zeer snel gaat (300.000 kilometer/seconde), zal de lichtklok voor elke seconde die door een gewone klok wordt gemeten een zeer groot aantal keren "tikken".

Om de wiskunde te vergemakkelijken, zullen we zeggen dat de paal een halve kilometer lang is. Dus als we bij de lichtklok staan die naast de grote telescoop op de Noordpool is gebouwd, zullen we zien dat het licht voor elke "tik" van de lichtklok een kilometer aflegt. Omdat de afgelegde afstand, d, gelijk is aan de snelheid vermenigvuldigd met de tijd, en de betreffende snelheid c is, hebben we de vergelijking:

d = ct

en we kunnen deze vergelijking voor t oplossen om te leren hoe lang in seconden elke "tik" is.

1 km = 300.000 km/seconde * t seconden

t seconden = 1 km/300.000 (km/seconde) = 1/300.000 seconden = 0,00000333...3 seconden

Met andere woorden, elke "tik" van de lichtklok zal 0,00000333...3 seconden duren.

Als een ruimteschip op een rechte lijn over de Noordpool vloog met een grote fractie van de lichtsnelheid, en het had een gelijkaardige klok, dan zouden de mensen die naar zijn doorgang keken zien dat de spiegel bovenop de paal zich van direct over het uitzendende licht had bewogen, dus het licht zou langs de lijn die h in het diagram gemarkeerd is reizen, en dan zou het de andere hypotenusa terug naar de basis van de paal volgen -- welke inmiddels enige afstand zou hebben bewogen aangezien het ruimteschip zich zo snel beweegt. Wij kunnen berekenen hoeveel tijd één tikje volgens de mensen op Aarde zou duren. We weten dat de pool van het ruimteschip een lengte van a heeft omdat het hetzelfde soort klok is als de mensen op de Noordpool gebruiken. We willen weten hoe lang het duurt om de klok van het ruimteschip één keer aan te vinken.

We weten dat het ruimteschip 1/2 r t' zal reizen terwijl de lichtknippering naar de spiegel toe gaat, en nog eens 1/2 r t' terwijl de lichtknippering naar beneden gaat naar de basis van de paal. Dus die berekening geeft ons de lengte van lijn b in de grafiek. We kennen a, zodat we h kunnen achterhalen aan de hand van de stelling van Pythagoras:

h = √(a2 + (rt' /2)²)

De totale afstand die het licht aflegt is dus 2 h of d = 2 √(a2 + (rt' /2)²).

We weten ook dat de snelheid van het licht, c, constant is. Het maakt niet uit wie het meet, het blijkt dezelfde snelheid te zijn. We kunnen dat feit dus gebruiken om op een andere manier te berekenen hoe lang het duurt voordat de lichtflits van de basis naar de top van de paal gaat en weer terug:

t' = d/c

Met andere woorden, d = c t' .

Zodat we kunnen schrijven

c t' = 2 √(a2 + (rt' /2)²)

of

1/2 c t' = √(a2 + (rt' /2)²)

Om de bovenstaande vergelijking op te lossen, zullen we dat moeten doen:

1. Vierkant aan beide zijden
2. Beide zijden delen door t' ²
3. Vermenigvuldig beide zijden met 4
4. Beide zijden delen door c2
5. Vereenvoudig c2 / c2
6. R2/c2 van beide zijden aftrekken
7. Neem de vierkantswortel van beide zijden
8. Vermenigvuldig beide zijden met t'.
9. Verdeel beide zijden door √(1-r2/c2)

Als we bovenstaande vergelijking oplossen, vinden we dat:

t' = 2a/(c√(1-r2/c2)

De tijd tussen tikken op de klok op de Noordpool is 2a/c, dus we kunnen dan schrijven:

t' = t/√(1-r2/c2)

Als t = 1 seconde, dan is t' = 1,1547 sec. als het ruimteschip met de helft van de lichtsnelheid reist.

Experimenteer met verschillende snelheden op: http://www.1728.org/reltivty.htm

Vragen en antwoorden

V: Wat is een lichtbel?

V: Wat is tijddilatatie?

Vraag: Hoe kunnen wij berekenen hoeveel tijd er in een ruimteschip vertraagd wordt?

V: Hoe werkt een lichtklok?

V: Welke vergelijking hebben wij nodig voor deze berekening?

V. Hoe houdt de stelling van Pythagoras verband met deze berekening?

Zoek op letter