Algebra | een onderdeel van wiskunde

Geschiedenis

Vroege vormen van algebra werden ontwikkeld door de Babyloniërs en de Griekse meetkundigen zoals Hero van Alexandrië. Het woord "algebra" is echter een Latijnse vorm van het Arabische woord Al-Jabr ("gieten") en komt van een wiskundeboek Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Essay on the Computation of Casting and Equation") geschreven in de 9e eeuw door een Perzische wiskundige, Muhammad ibn Mūsā al-Khwārizmī, een moslim geboren in Khwarizm in Oezbekistan. Hij floreerde onder Al-Ma'moun in Bagdad, Irak in 813-833 na Christus, en stierf rond 840 na Christus. Het boek werd in de 12e eeuw naar Europa gebracht en vertaald in het Latijn. Het boek kreeg toen de naam "Algebra". (De uitgang van de naam van de wiskundige, al-Khwarizmi, werd veranderd in een woord dat gemakkelijker uit te spreken was in het Latijn, en werd het Engelse woord algorithm).

Voorbeelden

Hier volgt een eenvoudig voorbeeld van een algebraprobleem:

Sue heeft 12 snoepjes, en Ann heeft 24 snoepjes. Ze besluiten te delen zodat ze evenveel snoepjes hebben. Hoeveel snoepjes krijgt ieder van hen?

Dit zijn de stappen waarmee u het probleem kunt oplossen:

1. Om hetzelfde aantal snoepjes te hebben, moet Ann wat aan Sue geven. Laat x {{displaystyle x} staan voor het aantal snoepjes dat Ann aan Sue geeft.
2. Sue's snoepjes, plus x {playstyle x} , moeten hetzelfde zijn als Ann's snoepjes min x {playstyle x} . Dit wordt geschreven als: 12 + x = 24 - x {Displaystyle 12+x=24-x}
3. Trek 12 af van beide zijden van de vergelijking. Dit geeft: x = 12 - x {\displaystyle x=12-x} . (Wat aan de ene kant van het gelijkheidsteken gebeurt, moet ook aan de andere kant gebeuren, wil de vergelijking nog kloppen. Dus in dit geval, toen 12 van beide zijden werd afgetrokken, was er een middelste stap van 12 + x - 12 = 24 - x - 12 {\displaystyle 12+x-12=24-x-12} . Nadat iemand zich hiermee vertrouwd heeft gemaakt, wordt de middelste stap niet meer opgeschreven).
4. Tel x op bij beide zijden van de vergelijking. Dit geeft: 2 x = 12 {Displaystyle 2x=12}
5. Deel beide zijden van de vergelijking door 2. Dit geeft x = 6 {displaystyle x=6} . Het antwoord is zes. Dit betekent dat als Ann 6 snoepjes aan Sue geeft, ze evenveel snoepjes hebben.
6. Om dit te controleren, zet u 6 terug in de oorspronkelijke vergelijking waar x {displaystyle x} was: 12 + 6 = 24 - 6 {displaystyle 12+6=24-6}.
7. Dit geeft 18 = 18 {Displaystyle 18=18} , wat waar is. Ze hebben nu elk 18 snoepjes.

Met wat oefening kan algebra worden gebruikt wanneer een probleem te moeilijk is om op een andere manier op te lossen. Problemen zoals het aanleggen van een snelweg, het ontwerpen van een mobiele telefoon of het vinden van een geneesmiddel voor een ziekte vereisen allemaal algebra.

Algebra schrijven

Zoals in de meeste delen van de wiskunde wordt het optellen van y bij z (of y plus z ) geschreven als y + z ;

Het aftrekken van z van y (of y minus z ) wordt geschreven als y - z ;

en het delen van y door z (of y over z ) wordt geschreven als y / z of y z .

In algebra kan het vermenigvuldigen van y {{displaystyle y} met z {{displaystyle z} (of y {{displaystyle y} maal z {{displaystyle z} ) op 3 verschillende manieren worden geschreven: y ⋅ z {{displaystyle ycdot z} , y ( z ) {\displaystyle y(z)} of gewoon y z {\displaystyle yz} . Al deze notaties betekenen hetzelfde: y {displaystyle y} maal z {displaystyle z} . Het symbool " × {times } "wordt niet gebruikt in algebra, omdat het te veel lijkt op de letter x , die vaak als variabele wordt gebruikt.

Wanneer we in de algebra een getal en een variabele met elkaar vermenigvuldigen, kunnen we gewoon het getal voor de letter schrijven: 5 ⋅ y ⟺ 5 y {displaystyle 5 y yiff 5y} . Als het getal 1 is, dan wordt het niet geschreven omdat 1 keer een willekeurig getal dat getal is ( 1 ⋅ y = y {displaystyle 1\cdot y=y} ) en dus is het niet nodig. En als het 0 is, kunnen we de termen volledig verwijderen, want 0 keer een willekeurig getal is nul ( 0 ⋅ y = 0 {\displaystyle 0\cdot y=0} ).

Terzijde: in algebra hoeft u de letters x ( ) en y ( ) niet te gebruiken. Variabelen zijn gewoon symbolen voor een onbekend getal of waarde, dus u kunt elke letter gebruiken voor een variabele (behalve e (getal van Euler) en i (denkbeeldige eenheid), want dat zijn wiskundige constanten). x en y zijn echter de meest gebruikelijke.

Functies en grafieken

Een belangrijk onderdeel van algebra is de studie van functies, omdat die vaak voorkomen in vergelijkingen die wij proberen op te lossen. Een functie is als een machine waar je een getal (of getallen) in kunt stoppen en een bepaald getal (of getallen) uit kunt halen. Bij het gebruik van functies kunnen grafieken krachtige hulpmiddelen zijn om de oplossingen van vergelijkingen te bestuderen.

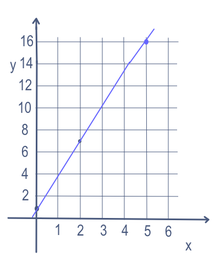
Een grafiek is een afbeelding met alle waarden van de variabelen die de vergelijking of ongelijkheid waar maken. Meestal is dit gemakkelijk te maken wanneer er slechts één of twee variabelen zijn. De grafiek is vaak een lijn, en als de lijn niet buigt of recht omhoog en omlaag gaat, kan hij worden beschreven met de basisformule y = m x + b {\displaystyle y=mx+b} . De variabele b is het y-afsnijpunt van de grafiek (waar de lijn de verticale as kruist) en m is de helling of steilheid van de lijn. Deze formule is van toepassing op de coördinaten van een grafiek, waarbij elk punt op de lijn wordt geschreven ( x {displaystyle x} , y {displaystyle y} ).

In sommige wiskundeproblemen, zoals de vergelijking voor een lijn, kan er meer dan één variabele zijn (x en y in dit geval). Om punten op de lijn te vinden, wordt één variabele veranderd. De veranderde variabele wordt de "onafhankelijke" variabele genoemd. Vervolgens wordt de wiskunde gedaan om een getal te maken. Het gemaakte getal wordt de "afhankelijke" variabele genoemd. Meestal wordt de onafhankelijke variabele geschreven als x {playstyle x} en de afhankelijke variabele als y {playstyle y}. bijvoorbeeld in y = 3 x + 1 {displaystyle y=3x+1} . Dit wordt vaak in een grafiek gezet, met een x-as (links en rechts) en een y-as (omhoog en omlaag). Het kan ook in functievorm worden geschreven: f ( x ) = 3 x + 1 {f(x)=3x+1} . Dus in dit voorbeeld kunnen we 5 invullen voor x {displaystyle x} en krijgen we y = 16 {displaystyle y=16}. . Door 2 in te vullen voor x {displaystyle x} krijgen we y = 7 {displaystyle y=7} . En 0 voor x {displaystyle x} zou y = 1 {displaystyle y=1} opleveren. Er zou dus een lijn lopen door de punten (5,16), (2,7), en (0,1) zoals te zien is in de grafiek rechts.

Als x {playstyle x} een macht van 1 heeft, is het een rechte lijn. Als het kwadraat of een andere macht is, is het krom. Als er een ongelijkheid wordt gebruikt ( < {{displaystyle <} of > {{displaystyle >} ), dan wordt meestal een deel van de grafiek gearceerd, boven of onder de lijn.

Regels

In de algebra zijn er enkele regels die kunnen worden gebruikt om vergelijkingen beter te begrijpen. Dit worden de regels van de algebra genoemd. Hoewel deze regels zinloos of vanzelfsprekend lijken, is het verstandig te begrijpen dat deze eigenschappen niet voor alle takken van de wiskunde gelden. Daarom is het nuttig te weten hoe deze axiomatische regels worden verklaard, alvorens ze als vanzelfsprekend aan te nemen. Alvorens over te gaan tot de regels, moet u nadenken over twee definities die zullen worden gegeven.

1. Tegenovergesteld: het tegenovergestelde van een {displaystyle a} is - een {displaystyle -a} .
2. Reciproque: het reciproque van een {displaystyle a} is 1 een {displaystyle {frac {1}{a}}} .

Commutatieve eigenschap van optelling

Commutatief' betekent dat een functie hetzelfde resultaat heeft als de getallen worden verwisseld. Met andere woorden, de volgorde van de termen in een vergelijking doet er niet toe. Wanneer twee termen (addenda) worden opgeteld, geldt de "commutatieve eigenschap van optellen". In algebraïsche termen geeft dit a + b = b + a {{{} .

Merk op dat dit niet geldt voor aftrekken (d.w.z. a - b ≠ b - a {{{³} b-a} behalve als a = b {{³} ).

Commutatieve eigenschap van vermenigvuldiging

Wanneer twee termen (factoren) worden vermenigvuldigd, geldt de "commutatieve eigenschap van vermenigvuldiging". In algebraïsche termen geeft dit a ⋅ b = b ⋅ a {{displaystyle a=b = a} .

Merk op dat dit niet geldt voor splitsing (d.w.z. a b ≠ b a {frac {a}{b}}} {frac {b}{a}}). , wanneer a ≠ 0 {{displaystyle a } } en b ≠ 0 {{displaystyle b} , behalve als a = b {{displaystyle a=b} ).

Associatieve eigenschap van optelling

Associatief verwijst naar het groeperen van getallen. De associatieve eigenschap van optellen houdt in dat het bij het optellen van drie of meer termen niet uitmaakt hoe deze termen zijn gegroepeerd. Algebraïsch gezien geeft dit a + ( b + c ) = ( a + b ) + c {{{empty a+(b+c)=(a+b)+c} . Merk op dat dit niet geldt voor aftrekken, bijv. 1 - ( 2 - 3 ) ≠ ( 1 - 2 ) - 3 {displaystyle 1-(2-3)\neq (1-2)-3} (zie distributieve eigenschap).

Associatieve eigenschap van vermenigvuldiging

De associatieve eigenschap van vermenigvuldiging houdt in dat het bij vermenigvuldiging van drie of meer termen niet uitmaakt hoe deze termen zijn gegroepeerd. Algebraïsch gezien geeft dit a ( b c ) = ( a b ) c {{(bc)=(ab)c} . Merk op dat dit niet geldt voor deling, bijvoorbeeld 1 / ( 2 / 4 ) ≠ ( 1 / 2 ) / 4 {\displaystyle 1/(2/4)\neq (1/2)/4} .

Verdelende eigenschap

De distributieve eigenschap stelt dat de vermenigvuldiging van een term met een andere term kan worden verdeeld. Bijvoorbeeld: a ( b + c ) = a b + a c {\displaystyle a(b+c)=ab+ac} . (Verwar dit niet met de associatieve eigenschappen! Bijvoorbeeld: a ( b + c ) ≠ ( a b ) + c {displaystyle a(b+c)\neq (ab)+c} .)

Additieve identiteit

"Identiteit" verwijst naar de eigenschap van een getal dat het gelijk is aan zichzelf. Met andere woorden, er bestaat een bewerking van twee getallen zodat deze gelijk is aan de variabele van de som. De additieve identiteitseigenschap stelt dat elk getal plus 0 gelijk is aan dat getal: a + 0 = a {a+0=a} . Dit geldt ook voor aftrekken: a - 0 = a {Displaystyle a-0=a} .

Multiplicatieve identiteit

De vermenigvuldigende identiteitseigenschap stelt dat elk getal maal 1 dat getal is: a ⋅ 1 = a {displaystyle a{cdot 1=a} . Dit geldt ook voor deling: a 1 = a {frac {a}{1}}=a} .

Additieve inverse eigenschap

De additieve inverse eigenschap is zoiets als het tegenovergestelde van de additieve identiteit. Wanneer we een getal en zijn tegengestelde optellen, is het resultaat 0. Algebraïsch staat er het volgende: a + - a = 0 {displaystyle a+-a=0}. , wat hetzelfde is als a - a = 0 {displaystyle a-a=0} . Bijvoorbeeld, de additieve inverse (of tegengestelde) van 1 is -1.

Multiplicatieve inverse eigenschap

De vermenigvuldigende inverse eigenschap betekent dat wanneer we een getal vermenigvuldigen met zijn inverse, de uitkomst 1 is. Algebraïsch staat er het volgende: a ⋅ 1 a = 1 {displaystyle a {frac {1}{a}}=1}. , wat hetzelfde is als a a = 1 {displaystyle {frac {a}{a}}=1} . Bijvoorbeeld, de vermenigvuldigende inverse (of gewoon inverse) van 2 is 1/2. Om de inverse van een breuk te krijgen, verwisselt u de teller en de noemer: de inverse van 2 3 {displaystyle {2}{3}}} is 3 2 {displaystyle {3}{2}} .

Gevorderde Algebra

Naast "elementaire algebra" of basisalgebra zijn er geavanceerde vormen van algebra, die op hogescholen en universiteiten worden onderwezen, zoals abstracte algebra, lineaire algebra en universele algebra. Dit omvat het gebruik van een matrix om vele lineaire vergelijkingen tegelijk op te lossen. Abstracte algebra is de studie van zaken die voorkomen in vergelijkingen, waarbij men verder gaat dan getallen, naar het meer abstracte met groepen getallen.

Veel wiskundeproblemen gaan over natuurkunde en techniek. In veel van deze natuurkundeproblemen is tijd een variabele. De gebruikte letter voor tijd is t . Het gebruik van de basisideeën uit de algebra kan helpen om een wiskundeprobleem terug te brengen tot zijn eenvoudigste vorm, waardoor het gemakkelijker wordt om moeilijke problemen op te lossen. Energie is e, kracht is f. , kracht is f , massa is m, versnelling is a. , versnelling is a en lichtsnelheid is soms c . Dit wordt gebruikt in een aantal beroemde vergelijkingen, zoals f = m a {displaystyle f=ma} en e = m c 2 {displaystyle e=mc^{2}}. (hoewel er meer complexe wiskunde dan algebra nodig was om tot die laatste vergelijking te komen).

Gerelateerde pagina's

• Lijst van wiskundeonderwerpen
• Volgorde van operaties
• Parabool
• Computer algebra systeem