AlegsaOnline.com

Stelling van Pythagoras: uitleg en formule voor rechthoekige driehoeken

Leer de stelling van Pythagoras: heldere uitleg, formule en voorbeelden voor rechthoekige driehoeken. Bereken hypotenusa en benen snel en eenvoudig.

Schrijver: Leandro Alegsa

17-02-2026

In de wiskunde is de stelling van Pythagoras een uitspraak over de zijden van een rechthoekige driehoek.

Een van de hoeken van een rechthoekige driehoek is altijd gelijk aan 90 graden. Deze hoek is de rechte hoek. De twee zijden naast de rechte hoek worden de benen genoemd en de andere zijde wordt de hypotenusa genoemd. De hypotenusa is de zijde tegenover de rechte hoek, en is altijd de langste zijde.

Formule en notatie

Als we de twee benen aanduiden met a en b en de hypotenusa met c, dan zegt de stelling van Pythagoras:

a² + b² = c²

Dit betekent dat het kwadraat (de lengte in het kwadraat) van de hypotenusa gelijk is aan de som van de kwadraten van de twee andere zijden.

Voorbeeld

Als a = 3 en b = 4, dan is c = √(3² + 4²) = √(9 + 16) = √25 = 5.
Als c = 13 en a = 5, dan is b = √(13² − 5²) = √(169 − 25) = √144 = 12.

Bewijs (kort overzicht)

Er zijn veel verschillende bewijzen van de stelling. Twee gangbare ideeën zijn:

Geometrisch (vierkanten): Leg vier congruente rechthoekige driehoeken in een vierkant zodat tussenruimte een kleiner vierkant vormt. Door gebieden te vergelijken komt men bij a² + b² = c².
Gelijkvormigheid van driehoeken: Door hoogtelijn van de rechte hoek naar de hypotenusa te tekenen ontstaan twee kleinere driehoeken die gelijkvormig zijn met de oorspronkelijke. Verhoudingen tussen de zijden leveren de stelling op.

Converse en toepassingen

De converse van de stelling van Pythagoras is ook waar: als in een driehoek de zijden a, b, c voldoen aan a² + b² = c², dan is de hoek tegenover zijde c een rechte hoek. Dit maakt de stelling een nuttig instrument om te controleren of een driehoek rechthoekig is.

Toepassingen zijn onder andere:

Berekenen van afstanden in de bouw en techniek.
De afstandsformule in het vlak: tussen punten (x1,y1) en (x2,y2) is √((x2−x1)² + (y2−y1)²), een directe toepassing van Pythagoras.
Computergraphics, navigatie en ingenieurswerk.

Pythagorese drietallen

Een Pythagorees drietal is een verzameling gehele getallen (a, b, c) die voldoen aan a² + b² = c². Bekende voorbeelden zijn (3,4,5) en (5,12,13). Een algemene manier om primitieve drietallen (zonder gemeenschappelijke delers) te construeren is met gehele getallen m en n (m > n):

a = m² − n²
b = 2mn
c = m² + n²

Algemene uitbreidingen

Wet van de cosinus: Voor elke driehoek met zijden a, b, c en hoek γ tussen a en b geldt c² = a² + b² − 2ab cos γ. Voor γ = 90° reduceert dit tot de stelling van Pythagoras.
Hogere dimensies: In de euclidische ruimte van hogere dimensies geldt dat de afstand tussen twee punten de wortel is van de som van de kwadraten van de verschillen in coördinaten — dit generaliseert het idee van Pythagoras.

Praktische aandachtspunten

Zorg dat alle lengtematen in dezelfde eenheid staan voordat je de formule toepast.
Als a² + b² < c² is de driehoek stomp (obtuse); als a² + b² > c² is de driehoek spits (acute).

De stelling van Pythagoras is dus een van de meest fundamentele en toepasbare resultaten in de meetkunde — eenvoudig te gebruiken, met vele bewijzen en brede toepassingen in wetenschap en techniek.

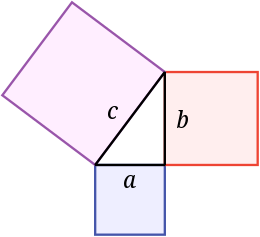
Stelling van Pythagoras De som van de oppervlakten van de twee vierkanten op de benen (a en b) is gelijk aan de oppervlakte van het vierkant op de schuine zijde (c).

Bewering van de theorie

De stelling van Pythagoras zegt dat de oppervlakte van een vierkant op de schuine zijde gelijk is aan de som van de oppervlakten van de vierkanten op de benen. In deze afbeelding is de oppervlakte van het blauwe vierkant, opgeteld bij de oppervlakte van het rode vierkant, de oppervlakte van het paarse vierkant. Ze werd genoemd naar de Griekse wiskundige Pythagoras:

Als de lengtes van de benen a en b zijn, en de lengte van de schuine zijde c, dan is a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

Soorten bewijzen

Er zijn veel verschillende bewijzen van deze stelling. Ze vallen in vier categorieën uiteen:

Die gebaseerd zijn op lineaire relaties: de algebraïsche bewijzen.
Die gebaseerd zijn op de vergelijking van oppervlakten: de geometrische bewijzen.
Deze zijn gebaseerd op de vectoroperatie.
Die gebaseerd zijn op massa en snelheid: de dynamische bewijzen.

Bewijs

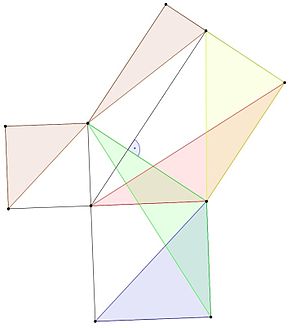
Een bewijs van de stelling van Pythagoras werd gevonden door een Griekse wiskundige, Eudoxus van Cnidus.

Het bewijs maakt gebruik van drie lemma's:

Driehoeken met dezelfde basis en hoogte hebben dezelfde oppervlakte.
Een driehoek met dezelfde basis en hoogte als een zijde van een vierkant heeft dezelfde oppervlakte als een helft van het vierkant.
Driehoeken met twee congruente zijden en één congruente hoek zijn congruent en hebben dezelfde oppervlakte.

Het bewijs is:

De blauwe driehoek heeft dezelfde oppervlakte als de groene driehoek, omdat hij dezelfde basis en hoogte heeft (lemma 1).
Groene en rode driehoeken hebben beide twee zijden gelijk aan zijden van dezelfde vierkanten, en een hoek gelijk aan een rechte hoek (een hoek van 90 graden) plus een hoek van een driehoek, dus ze zijn congruent en hebben dezelfde oppervlakte (lemma 3).
De oppervlakten van rode en gele driehoeken zijn gelijk omdat zij dezelfde hoogte en basis hebben (lemma 1).
De oppervlakte van de blauwe driehoek is gelijk aan de oppervlakte van de gele driehoek, omdat

A b l u e = A g r e e n = A r e d = A y e l l o w {{displaystyle}={{{color {blue}A_{blue}}={{{color {green}A_{green}}={{color {red}A_{red}}={{{color {yellow}A_{yellow}}}. ${\color {blue}A_{blue}}={\color {green}A_{green}}={\color {red}A_{red}}={\color {yellow}A_{yellow}}$

De bruine driehoeken hebben dezelfde oppervlakte om dezelfde redenen.
Blauw en bruin hebben elk de helft van de oppervlakte van een kleiner vierkant. De som van hun oppervlakten is gelijk aan de helft van de oppervlakte van het grotere vierkant. Daarom is de helft van de oppervlakte van kleine vierkanten gelijk aan de helft van de oppervlakte van het grotere vierkant, zodat hun oppervlakte gelijk is aan de oppervlakte van het grotere vierkant.

Bewijs met behulp van gelijkvormige driehoeken

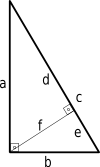
We kunnen een ander bewijs van de stelling van Pythagoras krijgen door gelijkvormige driehoeken te gebruiken.

d a = a c ⇒ a 2 = d c ( 1 ) {displaystyle {d}{a}}={frac {a}{c}}}}quad \Rightarrow \quad {a^{2}}={dc} (1)} ${\frac {d}{a}}={\frac {a}{c}}\quad \Rightarrow \quad {a^{2}}={dc}\quad (1)$

e b = b c ⇒ b 2 = e c ( 2 ) {\displaystyle {frac {e}{b}}={frac {b}{c}}}quad \Rightarrow \quad {b^{2}}={ec}quad (2)} ${\frac {e}{b}}={\frac {b}{c}}\quad \Rightarrow \quad {b^{2}}={ec}\quad (2)$

Voeg vanuit de afbeelding vergelijkingen (1) en (2) toe:

a 2 + b 2 = d c + e c ⇒ a 2 + b 2 = c ( d + e ) ⇒

${a^{2}}+{b^{2}}={dc+ec}\quad \Rightarrow a^{2}+b^{2}=c(d+e)\quad \Rightarrow a^{2}+b^{2}=c(c)$

En we krijgen:

c 2 = a 2 + b 2 . {\displaystyle c^{2}=a^{2}+b^{2},}. $c^{2}=a^{2}+b^{2}\,\!.$

Pythagoras triples

Pythagoreïsche drie-eenheden of tripletten zijn drie gehele getallen die voldoen aan de vergelijking a 2 + b 2 = c 2 {\displaystyle a^{2}+b^{2}=c^{2}}. $a^{2}+b^{2}=c^{2}$ .

De driehoek met zijden 3, 4 en 5 is een bekend voorbeeld. Als a=3 en b=4, dan is 3 2 + 4 2 = 5 2 {{displaystyle 3^{2}+4^{2}=5^{2}} $3^{2}+4^{2}=5^{2}$ omdat 9 + 16 = 25 {{displaystyle 9+16=25} $9+16=25$ . Dit kan ook worden weergegeven als 3 2 + 4 2 = 5. {\displaystyle {\sqrt {3^{2}+4^{2}}=5.} ${\sqrt {3^{2}+4^{2}}}=5.$

De drie-vier-vijf-driehoek werkt voor alle veelvouden van 3, 4 en 5. Met andere woorden, getallen als 6, 8, 10 of 30, 40 en 50 zijn ook Pythagorese driehoeken. Een ander voorbeeld van een driehoek is de driehoek 12-5-13, want 12 2 + 5 2 = 13 {{displaystyle {sqrt {12^{2}+5^{2}}}=13} ${\sqrt {12^{2}+5^{2}}}=13$ .

Een drievoud van Pythagoras dat geen veelvoud is van andere drieparen wordt een primitieve drievoud van Pythagoras genoemd. Elk primitief Pythagoreïsch drietal kan worden gevonden met behulp van de uitdrukking ( 2 m n , m 2 - n 2 , m 2 + n 2 ) {\displaystyle (2mn,m^{2}-n^{2},m^{2}+n^{2})}, maar er moet aan de volgende voorwaarden worden voldaan. $(2mn,m^{2}-n^{2},m^{2}+n^{2})$ maar de volgende voorwaarden moeten vervuld zijn. Ze leggen beperkingen op aan de waarden van m en n .

m {displaystyle m} en n {displaystyle n} zijn positieve gehele getallen.
m {displaystyle m} en n {displaystyle n} hebben geen gemeenschappelijke factoren behalve 1.
m en n hebben tegengestelde pariteit. m en n hebben tegengestelde pariteit wanneer m even is en n oneven, of m oneven is en n even.
m > n {displaystyle m>n} $m>n$ .

Als aan alle vier de voorwaarden is voldaan, dan vormen de waarden van m {displaystyle m} en n {displaystyle n} een primitieve Pythagoreïsche drievoud.

m = 2 {displaystyle m=2} $m=2$ en n = 1 {displaystyle n=1} $n=1$ vormen een primitieve Pythagoreïsche drievoud. De waarden voldoen aan alle vier de voorwaarden. 2 m n = 2 × 2 × 1 = 4 {displaystyle 2mn=2 maal 2 maal 1=4} $2mn=2\times 2\times 1=4$ , m 2 - n 2 = 2 2 - 1 2 = 4 - 1 = 3 {\displaystyle m^{2}-n^{2}=2^{2}-1^{2}=4-1=3} $m^{2}-n^{2}=2^{2}-1^{2}=4-1=3$ en m 2 + n 2 = 2 2 + 1 2 = 4 + 1 = 5 {\displaystyle m^{2}+n^{2}=2^{2}+1^{2}=4+1=5}. $m^{2}+n^{2}=2^{2}+1^{2}=4+1=5$ , zodat het drietal ( 3 , 4 , 5 ) {\displaystyle (3,4,5)} $(3,4,5)$ ontstaat.

Vragen en antwoorden

V: Wat is de stelling van Pythagoras?

A: De stelling van Pythagoras is een uitspraak over de zijden van een rechthoekige driehoek.

V: Welke hoek is in een rechthoekige driehoek altijd gelijk aan 90 graden?

A: Een van de hoeken van een rechthoekige driehoek is altijd gelijk aan 90 graden, dit wordt de rechte hoek genoemd.

V: Hoe worden de twee zijden naast de rechte hoek genoemd?

A: De twee zijden naast de rechte hoek worden de benen genoemd.

V: Hoe wordt de zijde tegenover de rechte hoek genoemd?

A: De zijde tegenover de rechte hoek wordt hypotenusa genoemd en is altijd de langste zijde.

V: Bestaat er een vergelijking om deze stelling te berekenen?

A: Ja, er bestaat een vergelijking voor de berekening van deze stelling die stelt dat "het kwadraat van de lengte van de schuine zijde gelijk is aan de som van de kwadraten van de lengten van de twee andere zijden".

V: Worden alle driehoeken met hoeken van 90 graden beschouwd als "rechtse" driehoeken?

A: Nee, niet alle driehoeken met hoeken van 90 graden worden beschouwd als "rechtse" driehoeken; alleen die waarvan één zijde (hypotenusa) langer is dan de andere twee zijden en aan het uiteinde een hoek van 90 graden vormt, kunnen als "rechtse" driehoeken worden beschouwd.