Lineaire regressie
Lineaire regressie is een manier om met behulp van wiskunde te bekijken hoe iets verandert als andere dingen veranderen. Een lineaire regressie gebruikt een afhankelijke variabele en een of meer verklarende variabelen om een rechte lijn te creëren. Deze rechte lijn staat bekend als een "regressielijn".
Lineaire regressie was de eerste van vele manieren om regressieanalyse uit te voeren. Modellen die lineair afhankelijk zijn van hun onbekende parameters zijn namelijk gemakkelijker te passen dan modellen die niet-lineair gerelateerd zijn aan hun parameters. Een ander voordeel van lineaire regressie is dat de statistische eigenschappen van de resulterende schatters gemakkelijker te bepalen zijn.
Lineaire regressie kent vele praktische toepassingen. De meeste toepassingen vallen in een van de volgende twee grote categorieën:
- Lineaire regressie kan worden gebruikt om een voorspellend model toe te passen op een reeks waargenomen waarden (gegevens). Dit is nuttig als het doel voorspelling, prognose of reductie is. Als na de ontwikkeling van een dergelijk model een extra waarde van X wordt gegeven zonder de bijbehorende waarde van y, kan het gepaste model worden gebruikt om een voorspelde waarde van y te maken (geschreven als
).
- Gegeven een variabele y en een aantal variabelen X1 , ..., Xp die verband kunnen houden met y, kan lineaire regressieanalyse worden toegepast om de sterkte van het verband tussen y en de Xj te kwantificeren, om te beoordelen welke Xj helemaal geen verband heeft met y, en om vast te stellen welke deelverzamelingen van de Xj overbodige informatie over y bevatten.
Lineaire regressiemodellen proberen de verticale afstand tussen de lijn en de gegevenspunten (de residuen) zo klein mogelijk te maken. Dit heet "de lijn aanpassen aan de gegevens". Vaak proberen lineaire regressiemodellen de som van de kwadraten van de residuen te minimaliseren (kleinste kwadraten), maar er bestaan ook andere manieren van passen. Deze omvatten het minimaliseren van het "gebrek aan passing" in een andere norm (zoals bij regressie van de kleinste absolute afwijkingen), of het minimaliseren van een gestrafte versie van de verliesfunctie van de kleinste kwadraten, zoals bij nokregressie. De benadering met de kleinste kwadraten kan ook worden gebruikt voor modellen die niet lineair zijn. Zoals hierboven uiteengezet, zijn de termen "kleinste kwadraten" en "lineair model" nauw met elkaar verbonden, maar het zijn geen synoniemen.
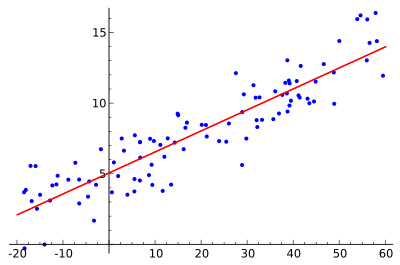
Het idee is om de rode curve te vinden, de blauwe punten zijn werkelijke steekproeven. Met lineaire regressie kunnen alle punten worden verbonden door een enkele, rechte lijn. In dit voorbeeld wordt eenvoudige lineaire regressie gebruikt, waarbij het kwadraat van de afstand tussen de rode lijn en elk monsterpunt wordt geminimaliseerd.
Gebruik
Economie
Lineaire regressie is het belangrijkste analyse-instrument in de economie. Zij wordt bijvoorbeeld gebruikt om de consumptie-uitgaven, de uitgaven voor vaste investeringen, de voorraadinvesteringen, de aankopen van de export van een land, de uitgaven voor invoer, de vraag naar liquide middelen, de vraag naar arbeid en het arbeidsaanbod te ramen.
Gerelateerde pagina's
- Curvefitting
- Logistische regressie
- Gewone kleinste kwadraten
Vragen en antwoorden
V: Wat is lineaire regressie?
A: Lineaire regressie is een manier om met behulp van wiskunde te bekijken hoe iets verandert als andere dingen veranderen. Het gebruikt een afhankelijke variabele en een of meer verklarende variabelen om een rechte lijn te creëren, die bekend staat als de "regressielijn".
V: Wat zijn de voordelen van lineaire regressie?
A: Modellen die lineair afhankelijk zijn van hun onbekende parameters zijn gemakkelijker te passen dan modellen die niet-lineair afhankelijk zijn van hun parameters. Bovendien zijn de statistische eigenschappen van de resulterende schatters gemakkelijker te bepalen.
V: Wat zijn enkele praktische toepassingen van lineaire regressie?
A: Lineaire regressie kan worden gebruikt om een voorspellend model toe te passen op waargenomen waarden (gegevens) om voorspellingen, prognoses of reducties te maken. Het kan ook worden gebruikt om de sterkte van relaties tussen variabelen te kwantificeren en subsets van gegevens te identificeren die overbodige informatie over een andere variabele bevatten.
V: Hoe proberen lineaire regressiemodellen fouten te minimaliseren?
A: Lineaire regressiemodellen proberen de verticale afstand tussen de lijn en de gegevenspunten (de residuen) zo klein mogelijk te maken. Dit gebeurt door ofwel de som van de kwadraten van de residuen te minimaliseren (kleinste kwadraten), ofwel de passing in een andere norm te minimaliseren (kleinste absolute afwijkingen), ofwel een gestrafte versie van de verliesfunctie van de kleinste kwadraten te minimaliseren (nokregressie).
V: Is het mogelijk dat lineaire regressiemodellen niet gebaseerd zijn op de kleinste kwadraten?
A: Ja, het is mogelijk dat lineaire regressiemodellen niet gebaseerd zijn op de kleinste kwadraten, maar in plaats daarvan methoden gebruiken zoals het minimaliseren van de "lack of fit" in een andere norm (kleinste absolute afwijkingen) of het minimaliseren van een gestrafte versie van de verliesfunctie van de kleinste kwadraten (nokregressie).
V: Zijn "lineair model" en "kleinste kwadraten" synoniemen?
A: Nee, het zijn geen synoniemen. Hoewel ze nauw met elkaar verbonden zijn, verwijst "lineair model" specifiek naar het gebruik van een rechte lijn, terwijl "kleinste kwadraten" specifiek verwijst naar het minimaliseren van fouten door ervoor te zorgen dat de verticale afstand tussen de lijn en de gegevenspunten minimaal is.
Zoek in de encyclopedie