Valversnelling

Waarom zwaardere voorwerpen niet sneller vallen dan lichtere voorwerpen

Isaac Newton heeft berekend dat de resulterende kracht gelijk is aan massa maal versnelling, of in symbolen, F = m a {\displaystyle F=ma} . Dit kan herschreven worden tot a = F m {{\displaystyle a={\frac {F}{m}}} . Hoe groter de massa van het vallende voorwerp, hoe groter de aantrekkingskracht van de zwaartekracht die het naar de aarde trekt. In de bovenstaande vergelijking is dat F {\displaystyle F} . Het aantal keren dat de kracht groter of kleiner wordt is echter gelijk aan het aantal keren dat de massa groter of kleiner wordt, waarbij de verhouding constant blijft. In elke situatie annuleert F m {\displaystyle {F}{m}} tot de uniforme versnelling van ongeveer 9,8 m/s2. Dit betekent dat alle vrij vallende voorwerpen, ongeacht hun massa, met dezelfde snelheid versnellen.

Kijk eens naar de volgende voorbeelden:

a = 49 N 5 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {49,\mathrm {N}} }{5,\mathrm {kg}} =9,8,\mathrm {N/kg} =9,8,\mathrm {m/s^{2}} }

a = 147 N 15 k g = 9,8 N / k g = 9,8 m / s 2 {\displaystyle a={\frac {147,\mathrm {N} }{15,\mathrm {kg}} =9,8,\mathrm {N/kg} =9,8,\mathrm {m/s^{2}} }

Oppervlakte versnelling

Afhankelijk van de plaats valt een voorwerp aan het aardoppervlak met een versnelling tussen 9,76 en 9,83 m/s2 (32,0 en 32,3 ft/s2).

De aarde is niet precies bolvormig. Zij is vergelijkbaar met een "geplette" bol, waarbij de straal aan de evenaar iets groter is dan die aan de polen. Dit heeft tot gevolg dat de gravitatieversnelling aan de polen iets toeneemt (omdat wij dicht bij het middelpunt van de aarde zijn en de gravitatiekracht van de afstand afhangt) en aan de evenaar iets afneemt. Ook is, vanwege de centripetale versnelling, de versnelling ten gevolge van de zwaartekracht iets minder aan de evenaar dan aan de polen. Veranderingen in de dichtheid van het gesteente onder de grond of de aanwezigheid van bergen in de buurt kunnen de zwaartekrachtsversnelling licht beïnvloeden.

Hoogte

De versnelling van een voorwerp verandert met de hoogte. De verandering van de gravitatieversnelling met de afstand tot het middelpunt van de aarde volgt een omgekeerd-kwadraatwet. Dit betekent dat de gravitatieversnelling omgekeerd evenredig is met het kwadraat van de afstand tot het middelpunt van de aarde. Als de afstand wordt verdubbeld, neemt de gravitatieversnelling af met een factor 4. Als de afstand wordt verdrievoudigd, neemt de gravitatieversnelling af met een factor 9, enzovoort.

gravitatieversnelling ∝ 1 afstand 2 {\displaystyle {\mbox{gravitatieversnelling}}}

zwaartekrachtversnelling × afstand 2 = k {\displaystyle {\mbox{zwaartekrachtversnelling}}} keer {{\mbox{afstand}}^{2}} ={k}}

Aan het oppervlak van de Aarde is de versnelling ten gevolge van de zwaartekracht ruwweg 9,8 m/s2 (32 ft/s2). De gemiddelde afstand tot het middelpunt van de aarde is 6.371 km.

k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9,8}}

Met behulp van de constante k {\displaystyle k} kunnen we de gravitatieversnelling op een bepaalde hoogte berekenen.

zwaartekrachtversnelling = k afstand 2 {\displaystyle {\mbox{zwaartekrachtversnelling}}}:={\frac {k}{{afstand}^{2}}}

Voorbeeld: Bereken de versnelling als gevolg van de zwaartekracht 1000 km boven het aardoppervlak.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371}

Afstand tot het middelpunt van de aarde is 7.371 km.

gravitatieversnelling = 9,8 × 6371 2 7371 2 ≈ 7,3 {\displaystyle {\mbox{gravitatieversnelling}} = {\frac {{\mbox{9,8}}} maal {{\mbox{6371}}^{2}}{\mbox{7371}}^{2}}} {{\mbox{7371}}^{2}}} \fax 7,3}}

∴ De versnelling door de zwaartekracht op 1000 km boven het aardoppervlak bedraagt 7,3 m/s2 (24 ft/s2).

De zwaartekrachtversnelling op de lijn Kármán, de grens tussen de aardatmosfeer en de ruimte die op 100 km hoogte ligt, is slechts ongeveer 3% lager dan op zeeniveau.

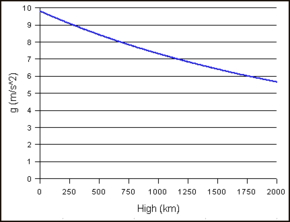
Verandering in gravitatieversnelling met de hoogte van een voorwerp