Parallellenpostulaat
In de meetkunde is het parallellenpostulaat een van de axioma's van de Euclidische meetkunde. Soms wordt het ook het vijfde postulaat van Euclides genoemd, omdat het het vijfde postulaat is in de Elementen van Euclides.
Het postulaat zegt dat:
Als je een lijnstuk snijdt met twee lijnen, en de twee binnenhoeken die de lijnen vormen zijn kleiner dan 180°, dan zullen de twee lijnen elkaar uiteindelijk raken als je ze lang genoeg verlengt.
Het gebied van de meetkunde dat alle axioma's van Euclides volgt, wordt Euclidische meetkunde genoemd. Meetkunde die niet alle axioma's van Euclides volgt, wordt niet-Euclidische meetkunde genoemd.
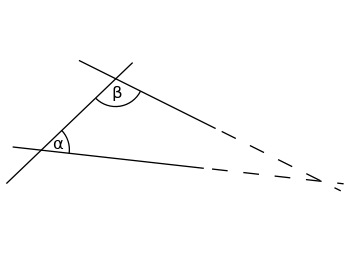
Als de som van de binnenhoeken α (alpha) en β (beta) kleiner is dan 180°, zullen de twee lijnen elkaar ergens snijden, als beide tot in het oneindige worden verlengd.
Geschiedenis
Sommige wiskundigen dachten dat het vijfde postulaat van Euclides veel langer en ingewikkelder was dan de andere vier postulaten. Velen van hen dachten dat het uit de andere eenvoudiger axioma's bewezen kon worden. Sommige wiskundigen kondigden aan dat zij de stelling uit de eenvoudiger stellingen hadden bewezen, maar zij bleken zich allen te hebben vergist.
Playfair's axioma
Een andere, meer recente stelling, bekend als Playfair's axioma, lijkt op het vijfde postulaat van Euclides. Het zegt dat:
Gegeven een rechte lijn en een punt niet op deze lijn, kan men slechts één rechte lijn door dit punt trekken die de andere rechte lijn niet zal ontmoeten.
In feite hebben wiskundigen ontdekt dat dit axioma niet alleen gelijk is aan het vijfde postulaat van Euclides, maar precies dezelfde implicaties heeft. Wiskundig worden de twee stellingen "equivalente" stellingen genoemd. Tegenwoordig wordt Playfair's axioma vaker door wiskundigen gebruikt dan Euclides' oorspronkelijke parallelle postulaat.
Niet-Euclidische meetkunde
Uiteindelijk hebben enkele wiskundigen geprobeerd nieuwe meetkunde te construeren zonder gebruik te maken van het axioma. Eén vorm van niet-Euclidische meetkunde wordt elliptische meetkunde genoemd. In de elliptische meetkunde wordt het parallellenpostulaat vervangen door een axioma dat stelt dat:
Gegeven een rechte lijn en een punt dat niet op deze lijn ligt, kan men geen rechte lijn door dit punt trekken die uiteindelijk niet de andere rechte lijn zal kruisen.
Wiskundigen ontdekten dat wanneer zij het vijfde postulaat van Euclides door dit axioma vervingen, zij nog steeds in staat waren veel van Euclides' andere stellingen te bewijzen. Eén manier om je elliptische meetkunde voor te stellen is door te denken aan het oppervlak van een wereldbol. Op een wereldbol lijken de lengtegraden evenwijdig te lopen aan de evenaar, maar bij de polen komen ze allemaal samen. Laat in de 19e eeuw werd aangetoond dat elliptische meetkunde consistent is. Dit bewees dat Euclides' vijfde postulaat niet onafhankelijk was van de andere postulaten. Hierna stopten wiskundigen meestal met het proberen te bewijzen van het vijfde postulaat uit de andere vier postulaten. In plaats daarvan begonnen veel wiskundigen andere meetkunde te bestuderen die niet het vijfde postulaat van Euclides volgen.
Een ander axioma waar wiskundigen soms Euclides' vijfde axioma door vervangen zegt dat:
Gegeven een rechte lijn en een punt dat niet op deze lijn ligt, kun je door dit punt minstens twee rechte lijnen trekken die uiteindelijk niet de andere rechte lijn zullen kruisen.
Dit wordt hyperbolische meetkunde genoemd.
Een andere meetkunde verwijdert eenvoudig het vijfde postulaat van Euclides en vervangt het door niets. Dit wordt neutrale meetkunde of absolute meetkunde genoemd.
Zoek in de encyclopedie