Waarschijnlijkheid ruimte
Waarschijnlijkheidsruimte is een wiskundig model dat wordt gebruikt om wetenschappelijke experimenten te beschrijven Een waarschijnlijkheidsruimte bestaat uit drie delen:
- Een voorbeeldruimte die alle mogelijke uitkomsten opsomt
- Een reeks gebeurtenissen. Elke gebeurtenis kent nul of meer resultaten
- Een functie die aan elke gebeurtenis waarschijnlijkheid toekent
Een resultaat is het resultaat van één enkele uitvoering van het model. Aangezien individuele uitkomsten wellicht weinig praktisch nut hebben, worden complexere gebeurtenissen gebruikt om groepen uitkomsten te karakteriseren. De verzameling van al deze gebeurtenissen is een σ-algebra F... 
Als de waarschijnlijkheidsruimte eenmaal is vastgesteld, wordt aangenomen dat "de natuur" zijn beweging maakt en een enkel resultaat, ω, uit de steekproefruimte Ω selecteert. Alle gebeurtenissen in F-stijl 
De prominente Sovjetwiskundige Andrej Kolmogorov introduceerde in de jaren dertig van de vorige eeuw het begrip kansberekening, samen met andere kansberekeningssystemen.
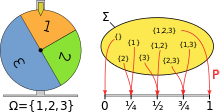
Het modelleren van een rad van fortuin met behulp van de waarschijnlijkheidsruimte
Vragen en antwoorden
V: Wat is een waarschijnlijkheidsruimte?
A: Een waarschijnlijkheidsruimte is een wiskundig model dat gebruikt wordt om wetenschappelijke experimenten te beschrijven. Het bestaat uit drie delen: een steekproefruimte die alle mogelijke uitkomsten opsomt, een reeks gebeurtenissen die nul of meer uitkomsten associëren, en een functie die waarschijnlijkheden toekent aan elke gebeurtenis.
V: Waaruit bestaat de steekproefruimte?
A: De steekproefruimte bestaat uit alle mogelijke uitkomsten, vaak geschreven als Ω {Omega}. en een uitkomst als ω {\displaystyle \omega }. .
V: Wat is een uitkomst?
A: Een uitkomst is het resultaat van een enkele uitvoering van het model.
V: Waarvoor worden gebeurtenissen gebruikt in kansruimten?
A: Gebeurtenissen worden gebruikt om groepen van uitkomsten te karakteriseren, omdat individuele uitkomsten in de praktijk weinig zin hebben. De verzameling van al deze gebeurtenissen wordt een σ-algebra genoemd, soms geschreven als F
Zoek in de encyclopedie