Heaviside-functie

De Heaviside-functie, H, is een niet-continue functie waarvan de waarde nul is voor een negatieve input en één voor een positieve input.

De functie wordt in de wiskunde van de controletheorie gebruikt om een signaal voor te stellen dat op een bepaald tijdstip wordt ingeschakeld en voor onbepaalde tijd ingeschakeld blijft. Zij werd genoemd naar de Engelsman Oliver Heaviside.

De Heaviside functie is de integraal van de Dirac delta functie: H′ = δ. Deze wordt soms geschreven als

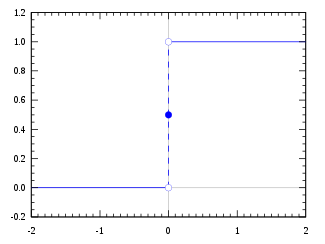
De Heaviside stapfunctie, gebruik makend van de half-maximum conventie

Discrete vorm

Wij kunnen ook een alternatieve vorm van de Heaviside-stappenfunctie definiëren als functie van een discrete variabele n:

H [ n ] = {0 , n < 0 1 , n ≥ 0 {Stijl H[n]={>begin{cases}0,&n<0\1,&n\geq 0{cases}} $H[n]={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}$

waarbij n een geheel getal is.

H ( x ) = lim z → x - ( ( | z | / z + 1 ) / 2 ) {Displaystyle H(x)=lim _{zrightarrow x^{-}}((|z|/z+1)/2)} $H(x)=\lim _{z\rightarrow x^{-}}((|z|/z+1)/2)$

De discrete-tijd eenheidsimpuls is het eerste verschil van de discrete-tijdstap

δ [ n ] = H [ n ] - H [ n - 1 ] . links[nrechts]=H[n]-H[n-1]. } $\delta \left[n\right]=H[n]-H[n-1].$

Deze functie is de cumulatieve sommatie van de Kronecker delta:

H [ n ] = ∑ k = - ∞ n δ [ k ] {\displaystyle H[n]=sum _{k=-[k]^{n}]delta [k]\,} $H[n]=\sum _{k=-\infty }^{n}\delta [k]\,$

waarbij

δ [ k ] = δ k , 0 {\displaystyle \delta [k]=\delta _{k,0}} $\delta [k]=\delta _{k,0}\,$

is de discrete eenheidsimpulsfunctie.

Voorstellingen

Vaak is een integrale voorstelling van de Heaviside stapfunctie nuttig:

H ( x ) = lim ϵ → 0 + - 1 2 π i ∫ - ∞ ∞ 1 τ + i ϵ e - i x τ d τ = lim ϵ → 0 + 1 2 π i ∫ - ∞ ∞ 1 τ - i ϵ e i x τ d τ . {Displaystyle H(x)=lim _{-epsilon \tot 0^{+}}-{1 \over 2 \pi \mathrm {i} }int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i}} \epsilon }^mathrm {e} ^{-[mathrm {i} x[mathrm {d}] \tau =lim _{\epsilon \tot 0^{+}}{1 \over 2 \pi \mathrm {i}} }int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }^{mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau . } $H(x)=\lim _{\epsilon \to 0^{+}}-{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau +\mathrm {i} \epsilon }\mathrm {e} ^{-\mathrm {i} x\tau }\mathrm {d} \tau =\lim _{\epsilon \to 0^{+}}{1 \over 2\pi \mathrm {i} }\int _{-\infty }^{\infty }{1 \over \tau -\mathrm {i} \epsilon }\mathrm {e} ^{\mathrm {i} x\tau }\mathrm {d} \tau .$

H(0)

De waarde van de functie op 0 kan worden gedefinieerd als H(0) = 0, H(0) = ½ of H(0) = 1.

H ( x ) = 1 + sgn ( x ) 2 = { 0 , x < 0 1 2 , x = 0 1 , x > 0. {\displaystyle H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}} $H(x)={\frac {1+\operatorname {sgn}(x)}{2}}={\begin{cases}0,&x<0\\{\frac {1}{2}},&x=0\\1,&x>0.\end{cases}}$

Verwante pagina's

Laplace-transformatie