Lawine-effect
Het lawine-effect ("aardverschuivingseffect") is een eigenschap van blokcijfers en cryptografische hash-algoritmen. Het is vaak gewenst in de cryptografie. Het effect zegt, dat veel van de output moet veranderen, zelfs als de input slechts een beetje verandert. In goede blokcijfers betekent dit: Een kleine verandering in de key of de plaintext moet een sterke verandering in de cijfertekst veroorzaken.
Dit betekent dat kleine veranderingen zich snel kunnen verspreiden, wanneer het algoritme gebruik maakt van iteraties. Elk bit van de output is dus afhankelijk van elk bit van de input.
De term lawine-effect werd voor het eerst gebruikt door Horst Feistel (Feistel 1973). Later werd het concept geïdentificeerd door Shannon's eigenschap van verwarring.
Als een blokcodering of cryptografische hasjfunctie niet in belangrijke mate voldoet aan het lawine-effect, dan heeft het een slechte randomisatie. Zo kan een cryptoanalist voorspellingen doen over de input, als hij alleen de output krijgt. Dit kan voldoende zijn om het algoritme geheel of gedeeltelijk te breken (te kraken).
Het is een van de primaire ontwerpdoelen wanneer mensen een sterke versleutelings- of cryptografische hashfunctie creëren. Ze proberen er een goed lawine-effect in op te bouwen. Wiskundig gezien maakt dit gebruik van het vlindereffect. Daarom zijn de meeste blokcijfers productcijfers. Het is ook de reden waarom hash-functies grote datablokken hebben.
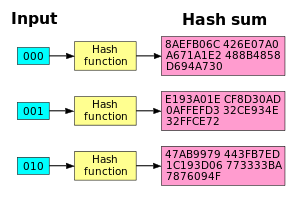
De SHA1 hasjfunctie heeft een goed lawine-effect. Wanneer een enkel bit wordt veranderd, wordt de hasjsom compleet anders.
Naam
De oorsprong van de naam zijn aardverschuivingen. Een kleine rots kan naar beneden vallen, met wat sneeuw meegaan en een verwoestende aardverschuiving veroorzaken. Het gesteente was klein, maar kon veel vernieling veroorzaken. Dat is hetzelfde als wat dit effect doet. Een kleine verandering in de input (het gesteente) zou de output (het landschap) moeten veranderen.
Strikt lawinecriterium
Het Strict Avalanche Criterium (SAC; een "sterk aardverschuivingscriterium") is een eigenschap van booleaanse functies. Het is van belang voor de cryptografie. Er wordt aan voldaan als alle uitvoerbits met een waarschijnlijkheid van 50 procent veranderen, als een enkele invoerbit wordt veranderd.
De SAC is gebouwd op de concepten van evolutionaire volledigheid en lawine. Het werd geïntroduceerd door Webster en Tavares in 1985. Tegenwoordig is het een vereiste voor elk modern cryptografisch systeem. Zo werd het bijvoorbeeld door alle finalisten van de AES-competitie tevreden gesteld.
Beetje onafhankelijkheidscriterium
Het Bitonafhankelijkheidscriterium (BIC; een criterium dat onafhankelijk is van het bit) is een criterium. Het gaat: Wanneer een enkel invoerbit wordt veranderd (omgekeerd), moeten twee uitvoerbits onafhankelijk van elkaar veranderen. Dit geldt voor alle bits.
Het zou bijvoorbeeld niet tevreden zijn als het ene uitgangsbit alleen verandert, terwijl het andere uitgangsbit ook verandert. Ze zouden alleen kunnen veranderen, omdat het ingangsbit veranderd is. Anders zouden de uitgangsbits van elkaar afhangen.
Gerelateerde pagina's
- Verwarring en verspreiding
Vragen en antwoorden
V: Wat is het lawine-effect?
A: Het lawine-effect (ook bekend als het "aardverschuivingseffect") is een eigenschap van blokcijfers en cryptografische hashfunctie-algoritmen die stelt dat een kleine verandering in de sleutel of klaartekst een sterke verandering in de cijfertekst moet veroorzaken.
V: Wie gebruikte voor het eerst de term "lawine-effect"?
A: De term lawine-effect werd voor het eerst gebruikt door Horst Feistel in 1973.
V: Wat is het verband met Shannons eigenschap van verwarring?
A: Het concept van het lawine-effect werd geïdentificeerd door Shannon's eigenschap van verwarring, die stelt dat als een blokcijfer of cryptografische hashfunctie hier niet in significante mate aan voldoet, deze een slechte randomisatie heeft en gedeeltelijk of volledig kan worden gebroken (gekraakt).
V: Wat zijn enkele ontwerpdoelstellingen bij het maken van sterke cijfers?
A: Wanneer mensen sterke cijfers maken, proberen zij er een goed lawine-effect in te bouwen met behulp van wiskundige principes zoals het vlindereffect. Daarom zijn de meeste blokcijfers productcijfers en hebben hashfuncties grote gegevensblokken.
V: Wat gebeurt er als een algoritme niet voldoet aan het lawine-effect?
A: Als een algoritme niet in aanzienlijke mate voldoet aan het lawine-effect, dan heeft het een slechte randomisatie en kan het gedeeltelijk of volledig worden gebroken (gekraakt) door cryptanalisten die voorspellingen kunnen doen over de invoer op basis van alleen de gegeven uitvoer.
V: Waarom gebruiken de meeste blokcijfers productcijfers?
A: De meeste blokcijfers gebruiken productcijfers omdat er goede avalance-effecten in worden ingebouwd met behulp van wiskundige principes zoals het vlindereffect.
V: Waarom hebben hashfuncties grote gegevensblokken?
A: Hashfuncties hebben grote datablokken omdat zij helpen goede avalantie-effecten in te bouwen met behulp van wiskundige principes zoals het vlindereffect.
Zoek in de encyclopedie