Algoritme

Het vergelijken van algoritmen

Er is meestal meer dan één manier om een probleem op te lossen. Er kunnen veel verschillende recepten zijn om een bepaald gerecht te maken dat er verschillend uitziet, maar uiteindelijk toch hetzelfde smaakt. Hetzelfde geldt voor algoritmen. Sommige van deze manieren zullen echter beter zijn dan andere. Als een recept veel ingewikkelde ingrediënten nodig heeft die je niet hebt, is het niet zo goed als een eenvoudig recept. Wanneer we kijken naar algoritmen als een manier om problemen op te lossen, willen we vaak weten hoe lang een computer erover zou doen om het probleem op te lossen met behulp van een bepaald algoritme. Wanneer we algoritmen schrijven, willen we dat ons algoritme zo weinig mogelijk tijd in beslag neemt, zodat we ons probleem zo snel mogelijk kunnen oplossen.

Bij het koken zijn sommige recepten moeilijker uit te voeren dan andere, omdat het meer tijd kost om ze af te maken of omdat er meer dingen zijn om bij te houden. Zo is het ook met algoritmen, en algoritmen zijn beter als ze voor de computer gemakkelijker te doen zijn. Wat de moeilijkheidsgraad van een algoritme meet, heet complexiteit. Als we vragen hoe ingewikkeld een algoritme is, willen we vaak weten hoe lang een computer erover zal doen om het probleem op te lossen dat we willen dat hij oplost.

Sorteren

Dit is een voorbeeld van een algoritme voor het sorteren van kaarten met kleuren erop in stapels van dezelfde kleur:

1. Raap alle kaarten op.
2. Neem een kaart uit je hand en kijk naar de kleur van de kaart.
3. Als er al een stapel kaarten van die kleur is, leg je deze kaart op die stapel.
4. Als er geen stapel kaarten van die kleur is, maak dan een nieuwe stapel van alleen deze kaartkleur.
5. Als er nog een kaart in je hand is, ga je terug naar de tweede stap.
6. Als er geen kaart meer in je hand is, dan zijn de kaarten gesorteerd. Je bent klaar.

Sorteren op nummers

Dit zijn voorbeelden van algoritmen om een stapel kaarten met veel verschillende getallen te sorteren, zodat de getallen op volgorde liggen.

De spelers beginnen met een stapel kaarten die nog niet gesorteerd zijn.

Eerste algoritme

Dit algoritme doorloopt de stapel kaarten, één kaart per keer. Deze kaart wordt vergeleken met de volgende kaart op de stapel. Merk op dat deze positie pas in stap 6 verandert. Dit algoritme heet bubble sort. Het is langzaam.

1. Als de stapel kaarten leeg is, of als er maar één kaart op ligt, is hij gesorteerd; je bent klaar.
2. Pak de stapel kaarten. Kijk naar de eerste kaart (de bovenste) van de stapel.
3. De kaart waar je naar kijkt is kaart A. De positie waar kaart A zich momenteel bevindt, is in stapel P.
4. Als er na kaart A geen kaarten meer in de stapel zitten, ga dan naar stap 8.
5. De volgende kaart op de stapel is kaart B.
6. Als kaart B een lager nummer heeft dan kaart A, verwissel dan de posities van kaarten A en B. Onthoud dat je dit gedaan hebt. Als je kaarten verwisselt, verander dan niet de positie P.
7. Als er nog een kaart in de stapel zit na positie P, kijk er dan naar; ga terug naar stap 3.
8. Als u in de laatste run geen kaarten van plaats heeft verwisseld, bent u klaar; de stapel kaarten is gesorteerd.
9. Ga anders terug naar stap 2.

Stap-voor-stap voorbeeld

Laten we een stapel kaarten nemen met de getallen "5 1 4 2 8", en deze sorteren van het kleinste getal naar het grootste met behulp van dit algoritme. In elke stap vergelijkt het algoritme de vetgedrukte elementen. De bovenkant van de stapel kaarten ligt aan de linkerkant.

Eerste doorgang:
( 5 1 4 2 8 ) → {\displaystyle \to } ( 1 5 4 2 8 ) Hier vergelijkt het algoritme de eerste twee elementen, en verwisselt ze.
( 1 5 4 2 8 ) → {\displaystyle \to } ( 1 4 5 2 8 )(
1 4 5 2 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 ) Deze elementen staan al op volgorde, dus het algoritme verwisselt ze niet.
Tweede pass:
( 1 4 2 5 8 ) → {\displaystyle \to } ( 1 4 2 5 8 )(
1 4 2 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Nu, de stapel kaarten is al gesorteerd, maar ons algoritme weet dit niet. Het algoritme heeft een hele pas nodig zonder enige verwisseling om te weten dat het gesorteerd is.
Derde pass:
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )(
1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
( 1 2 4 5 8 ) → {\displaystyle \to } ( 1 2 4 5 8 )
Tenslotte is de array gesorteerd, en kan het algoritme stoppen.

Geschiedenis

Dit is een eenvoudig te begrijpen algoritme voor sorteren. Computerwetenschappers noemden het Bubble sort, omdat kleinere elementen naar de top zullen stijgen, waarbij hun positie bij elke run verandert. Helaas is het algoritme niet erg goed, want het heeft veel tijd nodig (veel passes door de stapel kaarten) om te sorteren.

Tweede algoritme

Dit algoritme maakt gebruik van een ander idee. Soms is het oplossen van een probleem moeilijk, maar kan het probleem veranderd worden zodat het bestaat uit eenvoudiger problemen die gemakkelijker op te lossen zijn. Dit wordt recursie genoemd. Het is moeilijker te begrijpen dan het eerste voorbeeld, maar het zal een beter algoritme opleveren.

Basisidee

1. Als er geen kaarten op de stapel liggen, of als er maar één kaart op ligt, is hij gesorteerd, en ben je klaar.
2. Verdeel de stapel kaarten in twee helften van ongeveer dezelfde grootte. Als er een oneven aantal kaarten is, zal een van de twee stapels een kaart meer hebben dan de andere.
3. Sorteer elk van de twee stapels volgens dit algoritme (Begin voor elke stapel bij punt 1 van deze lijst).
4. Voeg de twee gesorteerde stapels samen, zoals hieronder beschreven.
5. Het resultaat is een gesorteerde stapel kaarten. U bent klaar.

Twee stapels samenvoegen

Dit werkt met twee stapels kaarten. Een ervan heet A, de andere heet B. Er is een derde stapel die aan het begin leeg is, genaamd C. Aan het eind zal deze de uitkomst bevatten.

1. Als stapel A of B leeg is, leg je alle kaarten van de stapel die niet leeg is bovenop stapel C; je bent klaar, stapel C is het resultaat van de samensmelting. (Opmerking: neem de hele stapel en leg die op stapel C; als u dit kaart voor kaart doet, verandert de volgorde en werkt het niet zoals het hoort).
2. Kijk naar de bovenste kaarten van stapel A en stapel B. Leg de kaart met het laagste nummer bovenop stapel C. Als stapel C geen kaarten bevatte, zit er nu één kaart in.
3. Als stapel A of stapel B kaarten over heeft, ga dan terug naar stap 1 om ze te sorteren.

Geschiedenis

John von Neumann ontwikkelde dit algoritme in 1945. Hij noemde het niet Sorteren op getallen, hij noemde het Mergesort. Het is een zeer goed algoritme voor sorteren, vergeleken met andere.

Derde algoritme

Het eerste algoritme doet er veel langer over om de kaarten te sorteren dan het tweede, maar het kan worden verbeterd (beter gemaakt). Als je naar bubble sort kijkt, zie je dat kaarten met hoge getallen vrij snel van de top van de stapel komen, maar dat kaarten met lage getallen onder aan de stapel er lang over doen om naar de top te komen. Om het eerste algoritme te verbeteren is hier het idee:

In plaats van twee kaarten te vergelijken die naast elkaar liggen, wordt er aan het begin een 'speciale' kaart gekozen. Alle andere kaarten worden dan vergeleken met deze kaart.

1. We beginnen met een stapel A. Er zijn twee andere stapels B en C, die later zullen worden aangemaakt.
2. Als stapel A geen kaarten heeft, of slechts één kaart, dan is het sorteren klaar.
3. Er wordt een kaart gekozen van stapel A, zo mogelijk willekeurig. Dit wordt een pivot genoemd.
4. Alle overgebleven kaarten van stapel A worden vergeleken met deze spil. Kaarten met een kleiner getal gaan naar stapel B, die met een gelijk of groter getal gaan naar stapel C.
5. Als er kaarten in de stapels B of C zitten, moeten deze stapels met hetzelfde algoritme gesorteerd worden (Begin bij pos 1 van deze lijst voor zowel stapel B als stapel C om de beurt).
6. Klaar. De gesorteerde stapel kaarten heeft eerst de gesorteerde stapel B, dan de spil, en dan de gesorteerde stapel C.

Geschiedenis

Dit algoritme is ontwikkeld door C.A.R. Hoare in 1960. Het is een van de meest gebruikte algoritmen voor sorteren vandaag de dag. Het wordt Quicksort genoemd.

Animatie die laat zien hoe een bubble sort werkt


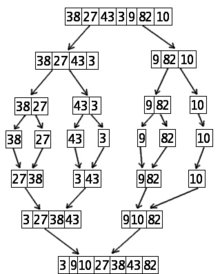
Sorteren van 7 getallen met behulp van het tweede algoritme voor sorteren op getallen (Mergesort)


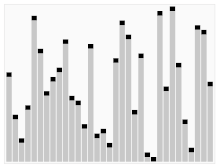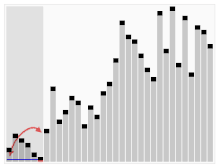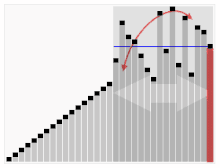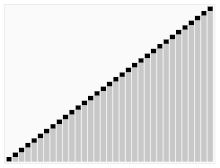
Het derde algoritme voor het sorteren van kaarten. Het element met de rode balk wordt gekozen als de spil. In het begin is dat het element helemaal rechts. Dit algoritme heet Quicksort.

Algoritmen samenstellen

Als de spelers kaarten hebben met kleuren en nummers erop, dan kunnen ze die sorteren op kleur en nummer als ze het "sorteren op kleuren" algoritme doen, dan het "sorteren op nummers" algoritme doen op elke gekleurde stapel, en dan de stapels bij elkaar leggen.

De sorteeralgoritmen op getallen zijn moeilijker uit te voeren dan de sorteeralgoritmen op kleuren, omdat de stappen misschien vele malen opnieuw moeten worden gedaan. Men zou zeggen dat sorteren op getallen complexer is.

Verwante pagina's

• Het Euclidisch algoritme werd meer dan 2000 jaar geleden gevonden. Het is in staat om de grootste gemene deler van twee getallen te vinden.