Kansdichtheid | functie die een continue kansverdeling karakteriseert

In de kansrekening en statistiek is een kansdichtheidsfunctie een functie die een continue kansverdeling karakteriseert. Voor een willekeurige variabele X wordt de kansdichtheidsfunctie van X soms geschreven als f X ( x ) $f_{X}(x)$ . De integraal van de kansdichtheidsfunctie in het interval [ a , b ] {\displaystyle [a,b]} $[a,b]$ geeft de kans dat een bepaalde willekeurige variabele met de gegeven dichtheid in het opgegeven interval ligt. Per definitie is de kansdichtheidsfunctie niet-negatief in zijn hele domein, waarop de integraal tot 1 sommeert.

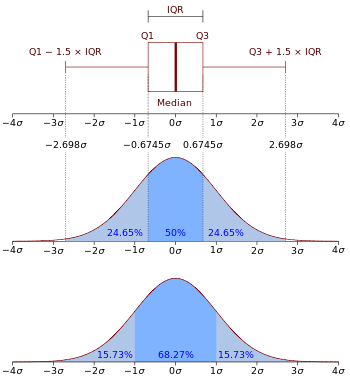
Boxplot en kansdichtheidsfunctie van een normale verdeling N(0, σ2 ) .

Waarschijnlijkheidsdichtheid versus waarschijnlijkheidsmassafunctie

De kansmassafunctie is voor een discrete kansverdeling wat de kansdichtheidsfunctie is voor een continue kansverdeling. De kansdichtheidsfunctie is nodig om te kunnen werken met continue verdelingen.

Een willekeurige variabele met een continue kansverdeling kan elke waarde binnen die verdeling aannemen. Het gooien van een dobbelsteen geeft de getallen 1 tot 6, met een waarschijnlijkheid van 1 6 {displaystyle {1}{6}}}. ${\tfrac {1}{6}}$ , maar dit is geen continue functie, want alleen de getallen 1 tot en met 6 zijn mogelijk.

Daarentegen zullen twee mensen niet dezelfde lengte of hetzelfde gewicht hebben. Met behulp van een kansdichtheidsfunctie is het mogelijk om de kans te bepalen voor mensen tussen 180 en 181 centimeter, of tussen 80 en 81 kilogram, hoewel er oneindig veel waarden tussen deze twee grenzen liggen.

Gerelateerde pagina's

Cumulatieve verdelingsfunctie

Vragen en antwoorden

V: Wat is een kansdichtheidsfunctie?

A: Een kansdichtheidsfunctie is een functie die een continue kansverdeling karakteriseert.

V: Hoe wordt de kansdichtheidsfunctie van een willekeurige variabele X geschreven?

A: De kansdichtheidsfunctie van X wordt soms geschreven als f_X(x).

Vraag: Wat stelt de integraal van de kansdichtheidsfunctie voor?

A: De integraal van de kansdichtheidsfunctie vertegenwoordigt de kans dat een gegeven willekeurige variabele met de gegeven dichtheid in een gegeven interval ligt.

V: Is de kansdichtheidsfunctie altijd niet-negatief in zijn hele domein?

Antwoord: Ja, per definitie is de kansdichtheidsfunctie niet-negatief in zijn hele domein.

V: Sommeert integreren over een interval tot 1?

A: Ja, integreren over een interval sommeert tot 1.

V: Welk type verdeling kenmerkt een waarschijnlijkheidsdichtheidsfunctie?

A: Een waarschijnlijkheidsdichtheidsfunctie kenmerkt elke continue kansverdeling.