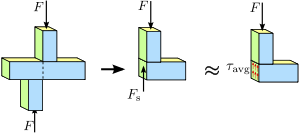Mechanische spanning
Stress is de kracht per oppervlakte-eenheid op een lichaam die de neiging heeft om het van vorm te doen veranderen.
Stress is een maat voor de interne krachten in een lichaam tussen de deeltjes. Deze interne krachten zijn een reactie op de externe krachten die op het lichaam worden uitgeoefend en die het lichaam doen scheiden, samenpersen of glijden. Externe krachten zijn ofwel oppervlaktekrachten ofwel lichaamskrachten. Stress is de gemiddelde kracht per oppervlakte-eenheid die een deeltje van een lichaam uitoefent op een aangrenzend deeltje, over een denkbeeldig oppervlak dat hen scheidt.
De formule voor uniaxiale normale stress is:
σ = F A. Een speelstijl...
waarbij σ de spanning is, F de kracht en A de oppervlakte.
In SI-eenheden wordt de kracht gemeten in newtons en de oppervlakte in vierkante meters. Dit betekent dat de spanning newtons per vierkante meter is, of N/m2. Spanning heeft echter een eigen SI-eenheid, de pascal. 1 pascal (symbool Pa) is gelijk aan 1 N/m2. In Imperiale eenheden wordt de spanning gemeten in pond per vierkante inch, wat vaak wordt afgekort tot "psi". De dimensie van de spanning is dezelfde als die van de druk.
In de continuümmechanica gedraagt het belaste vervormbare lichaam zich als een continuüm. Deze interne krachten worden dus continu verdeeld binnen het volume van het materiële lichaam. (Dit betekent dat de spanningsverdeling in het lichaam wordt uitgedrukt als een stukgewijze continue functie van ruimte en tijd). De krachten veroorzaken vervorming van de vorm van het lichaam. De vervorming kan leiden tot een permanente vormverandering of structureel falen als het materiaal niet sterk genoeg is.
Sommige modellen van continuümmechanica behandelen kracht als iets dat kan veranderen. Andere modellen kijken naar de vervorming van materie en vaste lichamen, omdat de eigenschappen van materie en vaste stoffen driedimensionaal zijn. Elke benadering kan andere resultaten opleveren. Klassieke modellen van de continuummechanica gaan uit van een gemiddelde kracht en bevatten geen goede "geometrische factoren". (De geometrie van het lichaam kan van belang zijn voor de manier waarop de spanning wordt verdeeld en hoe de energie zich opbouwt tijdens het uitoefenen van de externe kracht).
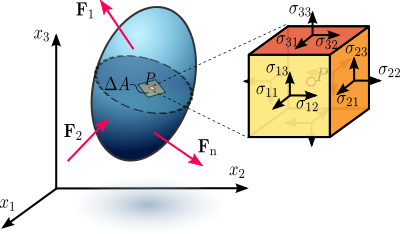
Figuur 1.1 Stress in een belastbaar vervormbaar materiaallichaam verondersteld als een continuüm.
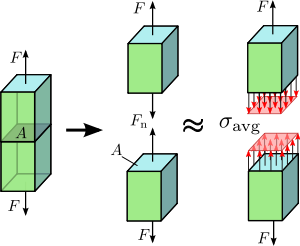
Figuur 1.2 Axiale spanning in een prismatische balk axiaal belast.
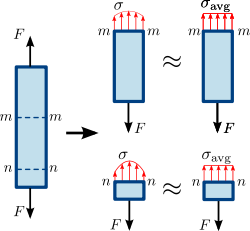
Figuur 1.3 Normale spanning in een prismatische (recht lid van uniforme doorsnede) staaf. De spanning of krachtverdeling in de dwarsdoorsnede van de staaf is niet noodzakelijkerwijs uniform. Echter, een gemiddelde normale spanning σ a v g geeft het beeld weer. }\,\! 
Figuur 1.4 Schuifspanning in een prismatische staaf. De spanning of krachtverdeling in de dwarsdoorsnede van de staaf is niet noodzakelijkerwijs uniform. Desalniettemin, een gemiddelde afschuifspanning τ a v g... }\,\! 
Schuifspanning
Meer informatie: Schuifspanning
Eenvoudige spanningen
In sommige situaties kan de spanning binnen een object worden beschreven door een enkel getal, of door een enkele vector (een getal en een richting). Drie van zulke eenvoudige stresssituaties zijn de uniaxiale normale stress, de eenvoudige schuifspanning en de isotrope normale stress.
Uniaxiale normale stress
De trekspanning (of spanning) is de spanningstoestand die leidt tot uitzetting; dat wil zeggen dat de lengte van een materiaal de neiging heeft om in de trekrichting toe te nemen. Het volume van het materiaal blijft constant. Wanneer gelijke en tegengestelde krachten op een lichaam worden uitgeoefend, dan wordt de spanning als gevolg van deze kracht trekspanning genoemd.
Daarom neemt in een uniaxiaal materiaal de lengte toe in de trekspanningsrichting en zullen de andere twee richtingen in omvang afnemen. Op de uniaxiale manier van spanning wordt de trekspanning geïnduceerd door trekkrachten. De trekspanning is het tegenovergestelde van de drukspanning.
Constructiedelen die onder directe spanning staan zijn touwen, bodemankers en -spijkers, bouten, enz. Balken die worden onderworpen aan buigmomenten kunnen zowel trekspanning als drukspanning en/of afschuifspanning bevatten.
De trekspanning kan worden verhoogd tot het bereiken van de treksterkte, namelijk de grenstoestand van de spanning.
Stress in eendimensionale lichamen
Alle echte objecten nemen de driedimensionale ruimte in beslag. Als twee dimensies echter zeer groot of zeer klein zijn in vergelijking met de andere, kan het object als eendimensionaal worden gemodelleerd. Dit vereenvoudigt de wiskundige modellering van het object. Tot de eendimensionale objecten behoren een stuk draad dat aan de uiteinden wordt geladen en van opzij wordt bekeken, en een metalen plaat die aan het gezicht wordt geladen en van dichtbij en door de dwarsdoorsnede wordt bekeken.
Gerelateerde pagina's
- Spanning
- Buigen
Vragen en antwoorden
V: Wat is stress?
A: Spanning is de kracht per oppervlakte-eenheid op een lichaam waardoor het van vorm verandert. Het is een maat voor de interne krachten in een lichaam tussen zijn deeltjes, en is de gemiddelde kracht per oppervlakte-eenheid die een deeltje van een lichaam uitoefent op een aangrenzend deeltje over een denkbeeldig oppervlak dat hen scheidt.
V: Hoe beïnvloeden externe krachten de spanning?
A: Externe krachten zijn ofwel oppervlaktekrachten ofwel lichaamskrachten, en zij veroorzaken vervorming van de vorm van het lichaam die kan leiden tot permanente vormverandering of structureel falen als het materiaal niet sterk genoeg is.
V: Wat is de formule voor eenassige normale spanning?
A: De formule voor éénassige normale spanning is σ = F/A, waarbij σ de spanning is, F de kracht en A de oppervlakte. In SI-eenheden wordt de kracht gemeten in newton en de oppervlakte in vierkante meter, wat betekent dat de spanning newton per vierkante meter (N/m2) zou zijn. Er bestaat echter een eigen SI-eenheid voor spanning, pascal (Pa) genaamd, die gelijk is aan 1 N/m2. In keizerlijke eenheden zou dit worden gemeten in pondkracht per vierkante inch (psi).
V: Wat veronderstelt de continuümmechanica over kracht?
A: Klassieke modellen van continuümmechanica gaan uit van een gemiddelde kracht en houden niet goed rekening met geometrische factoren - wat betekent dat zij geen rekening houden met hoe de geometrie beïnvloedt hoe energie wordt opgebouwd tijdens het uitoefenen van een externe kracht.
V: Hoe kunnen verschillende modellen verschillende resultaten geven bij de vervorming van materie en vaste lichamen?
A: Verschillende modellen kijken verschillend naar de vervorming van materie en vaste lichamen omdat de eigenschappen van materie en vaste lichamen driedimensionaal zijn - dus houdt elke benadering rekening met verschillende aspecten die tot verschillende resultaten kunnen leiden.
V: Hoe behandelt de continuümmechanica belaste vervormbare lichamen?
A: Continuümmechanica behandelt belaste vervormbare lichamen als continua - wat betekent dat interne krachten voortdurend worden verdeeld binnen het volume van het materiële lichaam in plaats van geconcentreerd te zijn op bepaalde punten zoals bij klassieke modellen.
Zoek in de encyclopedie