Cilinder (meetkunde) | een van de meest elementaire gebogen driedimensionale geometrische vormen
Een cilinder is een van de meest elementaire gebogen driedimensionale geometrische vormen, waarbij het oppervlak wordt gevormd door de punten op een vaste afstand van een bepaald lijnstuk, de as van de cilinder. De vorm kan worden beschouwd als een cirkelvormig prisma. Zowel het oppervlak als de vaste vorm die binnenin ontstaat, kan een cilinder worden genoemd. De oppervlakte en het volume van een cilinder zijn al sinds de oudheid bekend.
In de differentiaalmeetkunde wordt een cilinder ruimer gedefinieerd als een regeloppervlak dat wordt overspannen door een familie van parallelle lijnen met één parameter. Een cilinder waarvan de doorsnede een ellips, parabool of hyperbool is, wordt respectievelijk een elliptische, parabolische of hyperbolische cilinder genoemd.
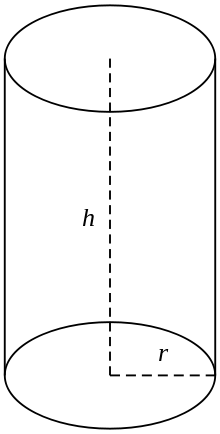
Een rechthoekige cilinder
Algemeen gebruik
In het algemeen wordt onder een cilinder verstaan een eindige doorsnede van een rechte cirkelvormige cilinder, d.w.z. de cilinder met de voortbrengende lijnen loodrecht op de bodems, met de uiteinden gesloten om twee cirkelvormige oppervlakken te vormen, zoals in de figuur (rechts). Indien de cilinder een straal r en lengte (hoogte) h heeft, dan is zijn volume gegeven door:
V = πr2 h
en de oppervlakte ervan is:
- de oppervlakte van de bovenkant (πr2 ) +
- de oppervlakte van de bodem (πr2 ) +
- de oppervlakte van de zijde (2πrh).
Daarom is de oppervlakte zonder de boven- of onderkant (lateraal gebied):
A = 2πrh.
Met de boven- en onderkant is de oppervlakte:
A = 2πr2 + 2πrh = 2πr(r + h).
Voor een gegeven volume heeft de cilinder met de kleinste oppervlakte h = 2r. Voor een gegeven oppervlakte heeft de cilinder met het grootste volume h = 2r, d.w.z. de cilinder past in een kubus (hoogte = diameter).
Volume
Een rechthoekige cilinder met een hoogte h eenheden en een basis met straal r eenheden met de coördinaatassen zo gekozen dat de oorsprong in het midden van een basis ligt en de hoogte wordt gemeten langs de positieve x-as. Een vlakke doorsnede op een afstand van x eenheden van de oorsprong heeft een oppervlakte van A(x) vierkante eenheden waarbij
of
Een volume-element, is een rechte cilinder met basisoppervlakte Awi vierkante eenheden en een dikte van Δi x eenheden. Dus als V kubieke eenheden het volume is van de rechter cilinder, door Riemann sommen,
Met behulp van cilindrische coördinaten kan het volume worden berekend door integratie over
Cilindrische doorsnede
Cilindrische doorsneden zijn de snijpunten van cilinders met vlakken. Voor een rechthoekige cilinder zijn er vier mogelijkheden. Een raakvlak aan de cilinder snijdt de cilinder in één rechte lijn. Evenwijdig aan zichzelf verplaatst, snijdt het vlak de cilinder ofwel niet, ofwel in twee evenwijdige lijnen. Alle andere vlakken snijden de cilinder in een ellips of, wanneer ze loodrecht op de as van de cilinder staan, in een cirkel.
Andere typen cilinders
Een elliptische cilinder, of cylindroïde, is een kwadratisch oppervlak, met de volgende vergelijking in cartesische coördinaten:
Deze vergelijking geldt voor een elliptische cilinder, een veralgemening van de gewone, cirkelvormige cilinder (a = b). Nog algemener is de gegeneraliseerde cilinder: de doorsnede kan een willekeurige kromme zijn.
De cilinder is een ontaarde kwadriek omdat ten minste één van de coördinaten (in dit geval z) niet in de vergelijking voorkomt.
Bij een schuine cilinder zijn het boven- en ondervlak van elkaar verwijderd.
Er zijn nog andere, meer ongebruikelijke soorten cilinders. Dit zijn de denkbeeldige elliptische cilinders:
de hyperbolische cilinder:
en de parabolische cilinder:
- ↑"MathWorld: Cylindric section".

Een elliptische cilinder

In de projectieve meetkunde is een cilinder gewoon een kegel waarvan de top op oneindig ligt, wat visueel overeenkomt met een cilinder in perspectief die een kegel naar de hemel lijkt te zijn.
Vragen en antwoorden
V: Wat is een cilinder?
A: Een cilinder is een driedimensionale geometrische vorm waarvan het oppervlak wordt gevormd door punten op een vaste afstand van een bepaald lijnstuk, bekend als de as van de cilinder. Men kan hem beschouwen als een cirkelvormig prisma en zowel het oppervlak als de vaste vorm die erin ontstaat, kan een cilinder worden genoemd.
V: Hoe lang is men al op de hoogte van de oppervlakte en het volume van cilinders?
A: De oppervlakte en het volume van cilinders zijn al sinds de oudheid bekend.
V: Wat zijn elliptische, parabolische en hyperbolische cilinders?
A: Elliptische, parabolische en hyperbolische cilinders zijn cilinders waarvan de doorsnede respectievelijk een ellips, parabool of hyperbool is.
V: Hoe wordt een cilinder gedefinieerd in de differentiaalmeetkunde?
A: In de differentiaalmeetkunde wordt een cilinder ruimer gedefinieerd als een regeloppervlak dat wordt overspannen door een familie van parallelle lijnen met één parameter.
V: Wat betekent het dat iets "geregeerd" is?
Antwoord: "Geregeld" betekent dat er op de een of andere manier rechte lijnen op zijn getekend.
V: Is er maar één type cilinder?
A: Nee, er zijn veel verschillende soorten cilinders, zoals elliptische, parabolische en hyperbolische cilinders, die allemaal een andere doorsnede hebben.
Zoek in de encyclopedie










