Elementaire algebra

Elementaire algebra is de meest elementaire vorm van algebra die aan studenten wordt onderwezen. Het is vaak een van de volgende gebieden van de wiskunde die aan studenten wordt onderwezen na het rekenen. Terwijl in het rekenen alleen getallen en operatoren zoals +, -, ×, en ÷ voorkomen; in algebra, worden variabelen (zoals a, x, y) gebruikt om voor getallen te staan. Dit is nuttig omdat:

Het laat mensen problemen over "onbekende" getallen oplossen. Dit betekent dat men leert over vergelijkingen en hoe deze op te lossen (bijvoorbeeld, "vind een getal x waarbij 3 x + 1 = 10 {\playstyle 3x+1=10} $3x+1=10$ ").
Het laat toe de regels te veralgemenen vanuit de rekenkunde. Terwijl sommige studenten begrijpen dat 3 + 4 = 4 + 3 {\playstyle 3+4=4+3} $3+4=4+3$ Het helpt om te bewijzen dat a + b = b + a {\playstyle a+b=b+a} voor alle a en b. Dit maakt algebra een goede stap om te leren over abstractie (het leren van algemene ideeën uit vele voorbeelden).
Het helpt mensen te begrijpen en functionele relaties te creëren (ook wel oorzaak en gevolg genoemd). Een voorbeeld hiervan is "als er x kaartjes worden verkocht, dan is de winst 3 x - 10 {\playstyle 3x-10} $3x-10$ dollars".

Deze drie zijn de belangrijkste onderdelen van elementaire algebra. Elementaire algebra wordt vaak gebruikt in vele andere vakken, zoals de wetenschap, het bedrijfsleven en de bouw. Abstracte algebra, een veel geavanceerder onderwerp, wordt over het algemeen laat op de universiteit onderwezen.

Eenvoudige algebra problemen

Als een vergelijking maar één getal heeft dat onbekend is, is het soms gemakkelijk op te lossen. Het onbekende getal heet "x":

2 x + 4 = 12. 2x+4=12.\,} $2x+4=12.\,$

Om een eenvoudige vergelijking met één onbekend bedrag op te lossen, tel je af, vermenigvuldig je of deel je beide zijden van de vergelijking met hetzelfde getal om het onbekende bedrag, x, aan één kant van de vergelijking te zetten. Als x op zichzelf aan één kant staat, gebruik dan de rekenkunde om het bedrag aan de andere kant van de vergelijking te bepalen. Bijvoorbeeld door 4 af te trekken van beide zijden in de vergelijking hierboven:

2 x + 4 - 4 = 12 - 4 {\\an5} $2x+4-4=12-4\,$

Het krijgen:

2 x = 8... 2x = 8... $2x=8\,$

Beide zijden delen door 2:

2 x 2 = 8 2...speelstijl... ${\frac {2x}{2}}={\frac {8}{2}}\,$

Het krijgen:

x = 4. Speelstijl x=4.\,| $x=4.\,$

Het kan helpen om deze vergelijking te zien als een zaag of een balans, wat je aan de ene kant doet, moet je aan de andere kant doen en je hoofddoel is om x op zichzelf te krijgen.

Definities

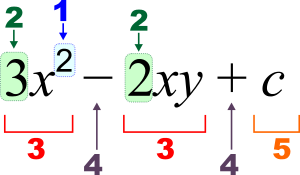
3 x 2 - 2 x y + c {\playstyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ heeft de volgende componenten:

1 : Exponent (vermogen), 2 : Coëfficiënt, 3 : term, 4 : operator, 5 : constant, x , y {\\\an8000} : $x,y$ variabelen

Vragen en antwoorden

V: Wat is elementaire algebra?

A: Elementaire algebra is de meest elementaire vorm van algebra die aan studenten wordt onderwezen. Het volgt meestal op rekenen en omvat het gebruik van variabelen (zoals a, x, y) voor getallen in vergelijkingen.

V: Wat zijn enkele toepassingen van elementaire algebra?

A: Elementaire algebra kan worden gebruikt om problemen met onbekende getallen op te lossen, regels uit de rekenkunde te veralgemenen, functionele relaties te begrijpen en te creëren, en wordt vaak gebruikt in vele andere vakken zoals wetenschap, bedrijfskunde en bouwkunde.

V: Hoe helpt elementaire algebra mensen om abstracte ideeën te begrijpen?

A: Elementaire algebra helpt mensen algemene ideeën te leren uit vele voorbeelden door te bewijzen dat a+b=b+a voor alle a en b. Hierdoor kunnen zij abstracte begrippen beter begrijpen.

V: Is abstracte algebra geavanceerder dan elementaire algebra?

A: Ja, abstracte algebra wordt over het algemeen laat op de universiteit onderwezen en is veel geavanceerder dan elementaire algebra.

V: Welke soorten vergelijkingen omvat elementaire algebra?

A: Elementaire algebra omvat vergelijkingen met variabelen (zoals a, x, y) die staan voor getallen en operatoren zoals +,-, × en ÷.
3x+1=10 {\displaystyle 3x+1=10}

V: Hoe kan inzicht in elementaire algebra helpen bij andere vakken?

A: Inzicht in elementaire algebra kan helpen bij andere vakken, zoals wetenschap, bedrijfskunde of bouwkunde, omdat het mensen in staat stelt problemen met onbekende getallen op te lossen en functionele relaties te leggen tussen verschillende variabelen.