Archimedische veelvlakken: definitie, eigenschappen en voorbeelden
Ontdek Archimedische veelvlakken: heldere definitie, unieke eigenschappen en aansprekende voorbeelden van deze regelmatige, niet‑platonische veelvlakken.
In de meetkunde is een Archimedisch veelvlak een convexe veelvlakvorm waarvan de zijvlakken bestaan uit regelmatige veelhoeken. Belangrijke kenmerken zijn:
- Elk gezicht is een regelmatige veelhoek.
- Alle hoekpunten (vertices) zijn onderling gelijk volgens de symmetrie van het veelvlak: het veelvlak is vertex-transitief — alle hoekpunten zien er hetzelfde uit.
- De vorm is noch een platonisch vast lichaam, noch een prisma, noch een antiprisma. Met andere woorden: niet alle gezichten zijn identiek (zoals bij Platons lichamen), en het is geen eenvoudige prisma- of antiprismatische bouw.
Hoeveel zijn er?
Afhankelijk van de manier van tellen bestaan er 13 of 15 Archimedische veelvlakken. De gebruikelijke telling geeft 13 verschillende types; twee daarvan, de snub cube en de snub dodecahedron, zijn chirale (handige/links-rechts) vormen waarvoor er twee spiegelbeeldvarianten bestaan die niet door rotatie congruent gemaakt kunnen worden. Tel je die spiegelbeelden apart, dan kom je op 15.
Herkomst en geschiedenis
De naam verwijst naar de Oudgriekse wiskundige Archimedes, die deze vormen waarschijnlijk in de 3e eeuw v.Chr. beschreef. De oorspronkelijke geschriften zijn verloren, maar Pappus van Alexandrië gaf in de 4e eeuw samenvattingen. Tijdens de Renaissance werden deze vormen opnieuw bestudeerd doordat kunstenaars en wiskundigen waarde hechtten aan zuivere vormen. Johannes Kepler voltooide rond 1620 veel van de classificatie en beschrijving van deze veelvlakken.
Bouwmethoden en relaties
Veel Archimedische veelvlakken kunnen worden geconstrueerd door bewerkingen op Platonische lichamen: truncatie (afsnijden van hoekpunten), rectificatie (afsnijden tot middens van edgen) of de snub-bewerking (draaiing en herschikking van vlakken). Hun symmetriegroepen zijn afleidbaar van die van de onderliggende Platonische lichamen. De vormen zijn convex en voldoen aan de Euler-relatie V − E + F = 2.
Voorbeelden en toepassingen
Bekende voorbeelden zijn onder meer het truncated icosahedron (de vorm van een voetbal of het fullereen C60, ook wel “buckyball” genoemd), de cuboctahedron, de icosidodecahedron, en meerdere truncaties en uitgebreide varianten van de vijf Platonsche lichamen. Archimedische veelvlakken komen voor in architectuur, kunst, kristallografie en scheikunde (bijvoorbeeld in de structuur van bepaalde moleculen en fullerenen).
Dualen
De duale veelvlakken van de Archimedische veelvlakken vormen een aparte familie: de Catalan-lichamen. Die zijn meestal niet regelmatig wat de gezichten betreft, maar hebben wel de symmetrieën die overeenkomen met de Archimedische vormen.
Overzicht van de 13 standaard Archimedische veelvlakken
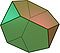
- Truncated tetrahedron
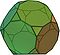
- Cuboctahedron
- Truncated cube
- Truncated octahedron
- Rhombicuboctahedron
- Truncated cuboctahedron (great rhombicuboctahedron)
- Snub cube (chiraal)
- Icosidodecahedron
- Truncated dodecahedron
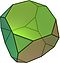
- Truncated icosahedron
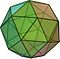
- Rhombicosidodecahedron
- Truncated icosidodecahedron (great rhombicosidodecahedron)
- Snub dodecahedron (chiraal)
Om een Archimedisch veelvlak te construeren zijn ten minste twee verschillende regelmatige veelhoeken nodig: dat onderscheidt deze lichamen van de Platonische lichamen (waar alle gezichten gelijk zijn) en van eenvoudige prisma's/antiprismata.
Samengevat: Archimedische veelvlakken zijn rijke, symmetrische en goed bestudeerde ruimtelijke figuren — geen Platonische lichamen, geen prisma's/antiprismata — met fraaie toepassingen in wetenschap en kunst.
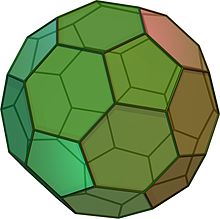
Een afgeknotte icosaëder lijkt op een voetbal. Hij is gemaakt van 12 gelijkzijdige vijfhoeken en 20 regelmatige zeshoeken. Het heeft 60 hoekpunten en 90 ribben. Het is een Archimedisch vast lichaam
Eigenschappen
- Archimedische vaste lichamen zijn gemaakt van regelmatige veelhoeken, daarom hebben alle ribben dezelfde lengte.
- Alle Archimedische vaste lichamen kunnen worden verkregen uit Platonische vaste lichamen, door de randen van het platonisch vaste lichaam te "snijden".
- Het type veelhoeken dat elkaar in een hoek ("hoekpunt") ontmoet, kenmerkt zowel het archimedische als het platonische vast lichaam
Verband met Platonische vaste lichamen
De Platonische vaste lichamen kunnen in Archimedische vaste lichamen worden veranderd door een aantal regels voor hun constructie te volgen.
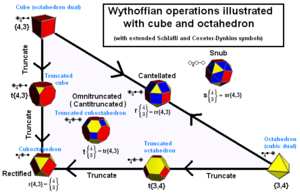
De vaste lichamen van Archimedes kunnen worden geconstrueerd als generatorposities in een caleidoscoop
Lijst van Archimedische vaste lichamen
Hier volgt een lijst van alle vaste lichamen van Archimedes
| Afbeelding | Naam | Gezichten | Type | Randen | Vertices |
|
| Afgeknotte tetraëder | 8 | 4 driehoeken 4 zeshoeken | 18 | 12 |
|
| 14 | 8 driehoeken 6 vierkanten | 24 | 12 | |
|
| Afgeknotte kubus | 14 | 8 driehoeken 6 achthoeken | 36 | 24 |
|
| 14 | 6 vierkanten 8 zeshoeken | 36 | 24 | |
|
| Rhombicuboctahedron | 26 | 8 driehoeken 18 pleinen | 48 | 24 |
|
| Afgeknotte kuboctaëder | 26 | 12 vierkanten 8 zeshoeken 6 achthoeken | 72 | 48 |
|
| Snub cube (2 gespiegelde versies) | 38 | 32 driehoeken 6 vierkanten | 60 | 24 |
|
| Icosidodecahedron | 32 | 20 driehoeken 12 vijfhoeken | 60 | 30 |
|
| Afgeknotte dodecaëder | 32 | 20 driehoeken 12 decagons | 90 | 60 |
|
| 32 | 12 vijfhoeken 20 hexagons | 90 | 60 | |
|
| Rhombicosidodecahedron | 62 | 20 driehoeken30 vierkanten12 | 120 | 60 |
|
| Afgeknotte icosidodecaëder | 62 | 30 vierkanten 20 hexagons 12 decagons | 180 | 120 |
|
| Snub dodecaëder (2 gespiegelde versies) | 92 | 80 driehoeken 12 vijfhoeken | 150 | 60 |
Vragen en antwoorden
V: Wat is een Archimedisch massief?
A: Een Archimedisch veelvlak is een convexe vorm van veelhoeken met de eigenschappen dat elk vlak een regelmatige veelhoek is, dat alle hoeken er hetzelfde uitzien en dat het geen platonisch veelvlak, prisma of antiprisma is.
V: Hoeveel Archimedische vaste lichamen zijn er?
A: Afhankelijk van hoe men ze telt, zijn er dertien of vijftien Archimedesische veelvlakken.
V: Wie heeft de Archimedische vaste lichamen ontdekt?
A: De Archimedische vaste lichamen zijn genoemd naar de Oudgriekse wiskundige Archimedes, die ze waarschijnlijk in de 3e eeuw voor Christus ontdekte.
V: Wat deed Pappus van Alexandrië met de geschriften van Archimedes?
A: Pappus van Alexandrië vatte in de 4e eeuw de geschriften van Archimedes over de vaste lichamen van Archimedes samen.
V: Waarom herontdekten kunstenaars en wiskundigen de vaste lichamen van Archimedes tijdens de Renaissance?
A: Tijdens de Renaissance waardeerden kunstenaars en wiskundigen zuivere vormen, en de vaste lichamen van Archimedes werden beschouwd als zuivere vormen.
V: Wanneer voltooide Johannes Kepler de zoektocht naar alle Archimedische vaste lichamen?
A: Johannes Kepler heeft de zoektocht naar alle Archimedische vaste lichamen waarschijnlijk rond 1620 voltooid.
V: Wat is er nodig om een Archimedisch massief te construeren?
A: Voor de constructie van een Archimedisch veelvlak zijn ten minste twee verschillende veelhoeken nodig.
Zoek in de encyclopedie