Standaardafwijking | een getal dat wordt gebruikt om aan te geven hoe de metingen voor een groep zijn verspreid van het gemiddelde
De standaardafwijking is een getal dat aangeeft hoe de metingen voor een groep uit elkaar liggen ten opzichte van het gemiddelde (gemiddelde of verwachte waarde). Een lage standaardafwijking betekent dat de meeste getallen dicht bij het gemiddelde liggen, terwijl een hoge standaardafwijking betekent dat de getallen meer verspreid liggen.
De gerapporteerde foutmarge is gewoonlijk tweemaal de standaardafwijking. Wetenschappers rapporteren gewoonlijk de standaardafwijking van getallen ten opzichte van het gemiddelde getal in experimenten. Zij besluiten vaak dat alleen verschillen groter dan twee of drie keer de standaardafwijking belangrijk zijn. De standaardafwijking is ook nuttig bij geld, waar de standaardafwijking van de verdiende rente aangeeft hoe verschillend de verdiende rente van één persoon kan zijn van het gemiddelde.
Vaak kan slechts een steekproef of een deel van een groep worden gemeten. Dan kan een getal dat dicht bij de standaardafwijking voor de hele groep ligt, worden gevonden door een iets andere vergelijking, die de standaardafwijking van de steekproef wordt genoemd en hieronder wordt uitgelegd. In dat geval wordt de standaardafwijking van de hele groep weergegeven door de Griekse letter 

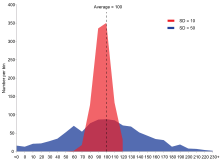
Voorbeeld van twee steekproefpopulaties met hetzelfde gemiddelde en verschillende standaardafwijkingen. Rode populatie heeft gemiddelde 100 en SD 10; blauwe populatie heeft gemiddelde 100 en SD 50.
.png)
Een plot van een normale verdeling (of bell curve). Elke gekleurde band heeft een breedte van één standaardafwijking.
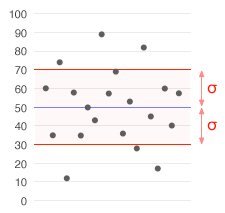
Een gegevensreeks met een gemiddelde van 50 (in blauw) en een standaardafwijking (σ) van 20.
Basisvoorbeeld
Beschouw een groep met de volgende acht getallen:
Deze acht getallen hebben een gemiddelde van 5:
Om de standaarddeviatie van de populatie te berekenen, zoekt u eerst het verschil van elk getal in de lijst met het gemiddelde. Kwadrateer vervolgens het resultaat van elk verschil:
Bereken vervolgens het gemiddelde van deze waarden (som gedeeld door het aantal getallen). Neem tenslotte de vierkantswortel:
Het antwoord is de standaarddeviatie van de populatie. De formule geldt alleen als de acht getallen waarmee we begonnen de hele groep vormen. Als zij slechts een deel van de willekeurig gekozen groep zijn, dan kunnen wij een onvertekende schatting krijgen van wat de standaardafwijking van de populatie is door te delen door 7 (dat is n - 1) in plaats van 8 (dat is n) in de onderste (noemer) van bovenstaande formule. Het antwoord is dan de (voor vertekening gecorrigeerde) standaardafwijking van de steekproef. Dit wordt de Bessel-correctie genoemd. Wij gebruiken deze correctie vaak omdat de steekproefvariantie, d.w.z. het kwadraat van de standaardafwijking van de steekproef, een onvertekende schatter is van de populatievariantie, met andere woorden, de verwachte waarde of het langetermijngemiddelde van de steekproefvariantie is gelijk aan de (werkelijke) populatievariantie. Het is echter niet zo dat de standaarddeviatie van de steekproef een onvertekende schatter is van de standaarddeviatie van de populatie.[1] Hoewel de correctie van Bessel een onvertekende schatter is van de variantie, heeft deze schatter wel een hogere gemiddelde kwadratische fout dan de vertekende schatter, of met andere woorden, de vertekende schatter (dat wil zeggen delen door n in plaats van n-1) ligt gemiddeld dichter bij de werkelijke waarde.
Meer voorbeelden
Hier is een iets moeilijker voorbeeld uit de praktijk: De gemiddelde lengte voor volwassen mannen in de Verenigde Staten is 70", met een standaardafwijking van 3". Een standaardafwijking van 3" betekent dat de meeste mannen (ongeveer 68%, uitgaande van een normale verdeling) een lengte hebben die 3" langer tot 3" korter is dan het gemiddelde (67"-73") - één standaardafwijking. Bijna alle mannen (ongeveer 95%) hebben een lengte die 6" langer tot 6" korter is dan het gemiddelde (64"-76") - twee standaardafwijkingen. Drie standaardafwijkingen omvatten alle getallen voor 99,7% van de onderzochte steekproefpopulatie. Dit geldt als de verdeling normaal (klokvormig) is.
Als de standaardafwijking nul zou zijn, dan zouden alle mannen precies 70" lang zijn. Als de standaardafwijking 20" zou zijn, dan zouden sommige mannen veel langer of veel korter zijn dan het gemiddelde, met een typisch bereik van ongeveer 50"-90".
Een ander voorbeeld: elk van de drie groepen {0, 0, 14, 14}, {0, 6, 8, 14} en {6, 6, 8, 8} heeft een gemiddelde (mean) van 7. Maar hun standaardafwijkingen zijn 7, 5, en 1. De derde groep heeft een veel kleinere standaardafwijking dan de andere twee, omdat de getallen allemaal dicht bij 7 liggen. In het algemeen vertelt de standaardafwijking ons hoe ver de rest van de getallen van het gemiddelde af ligt, en deze heeft dezelfde eenheden als de getallen zelf. Als bijvoorbeeld de groep {0, 6, 8, 14} de leeftijden is van een groep van vier broers in jaren, dan is het gemiddelde 7 jaar en de standaardafwijking 5 jaar.
De standaardafwijking kan dienen als maat voor de onzekerheid. In de wetenschap bijvoorbeeld helpt de standaardafwijking van een groep herhaalde metingen wetenschappers te weten hoe zeker ze zijn van het gemiddelde getal. Bij de beslissing of metingen van een experiment overeenkomen met een voorspelling, is de standaardafwijking van die metingen zeer belangrijk. Als het gemiddelde getal uit de experimenten te ver verwijderd is van het voorspelde getal (met de afstand gemeten in standaarddeviaties), dan is de geteste theorie misschien niet juist. Voor meer informatie, zie voorspellingsinterval.
Toepassingsvoorbeelden
Inzicht in de standaardafwijking van een reeks waarden stelt ons in staat te weten hoe groot het verschil met het "gemiddelde" is.
Weer
Neem als eenvoudig voorbeeld de gemiddelde dagelijkse hoge temperaturen voor twee steden, één in het binnenland en één bij de oceaan. Het is nuttig te begrijpen dat het bereik van de dagelijkse hoge temperaturen voor steden nabij de oceaan kleiner is dan voor steden in het binnenland. Deze twee steden kunnen elk dezelfde gemiddelde dagelijkse hoge temperatuur hebben. De standaardafwijking van de dagelijkse hoge temperatuur voor de kuststad zal echter kleiner zijn dan voor de stad in het binnenland.
Sport
Een andere manier om dit te zien is te kijken naar sportteams. In elke sport zijn er teams die in sommige dingen goed zijn en in andere niet. De teams die het hoogst genoteerd staan, vertonen niet veel verschillen in vaardigheden. Zij doen het goed in de meeste categorieën. Hoe lager de standaardafwijking van hun vaardigheden in elke categorie, hoe evenwichtiger en consistenter zij zijn. Teams met een hogere standaardafwijking zullen echter minder voorspelbaar zijn. Een team dat meestal slecht is in de meeste categorieën zal een lage standaardafwijking hebben. Een team dat meestal goed is in de meeste categorieën zal ook een lage standaarddeviatie hebben. Een team met een hoge standaardafwijking kan echter het type team zijn dat veel punten scoort (sterke aanval), maar ook het andere team veel punten laat scoren (zwakke verdediging).
Om op voorhand te weten welke teams zullen winnen, kan worden gekeken naar de standaardafwijkingen van de verschillende "statistieken" van de teams. Cijfers die afwijken van de verwachtingen kunnen sterke en zwakke punten met elkaar vergelijken om te laten zien welke redenen het belangrijkst zijn om te weten welk team zal winnen.
In de racerij wordt de tijd gemeten die een coureur nodig heeft om elke ronde rond het circuit af te leggen. Een coureur met een lage standaardafwijking van de rondetijden is consistenter dan een coureur met een hogere standaardafwijking. Deze informatie kan worden gebruikt om te begrijpen hoe een coureur de tijd die nodig is om een ronde af te leggen, kan verkorten.
Geld
In geld kan standaardafwijking het risico betekenen dat een koers stijgt of daalt (aandelen, obligaties, onroerend goed, enz.). Het kan ook het risico betekenen dat een groep koersen stijgt of daalt (actief beheerde beleggingsfondsen, indexbeleggingsfondsen of ETF's). Risico is een reden om beslissingen te nemen over wat te kopen. Risico is een getal dat mensen kunnen gebruiken om te weten hoeveel geld zij kunnen verdienen of verliezen. Naarmate het risico groter wordt, kan het rendement van een belegging hoger uitvallen dan verwacht (de "plus" standaarddeviatie). Een belegging kan echter ook meer geld verliezen dan verwacht (de "min" standaarddeviatie).
Iemand moest bijvoorbeeld kiezen tussen twee aandelen. Aandeel A had over de afgelopen 20 jaar een gemiddeld rendement van 10 procent, met een standaardafwijking van 20 procentpunten (pp). Aandeel B had de afgelopen 20 jaar een gemiddeld rendement van 12 procent, maar een hogere standaardafwijking van 30 procentpunten. Gezien het risico kan de persoon besluiten dat aandeel A de veiligere keuze is. Hoewel hij misschien niet zoveel geld verdient, zal hij waarschijnlijk ook niet veel geld verliezen. De persoon kan denken dat het 2 punten hogere gemiddelde van aandeel B de extra standaardafwijking van 10 procentpunten (groter risico of onzekerheid van het verwachte rendement) niet waard is.
Regels voor normaal verdeelde getallen
De meeste wiskundige vergelijkingen voor standaardafwijking gaan ervan uit dat de getallen normaal verdeeld zijn. Dit betekent dat de getallen op een bepaalde manier verdeeld zijn aan weerszijden van de gemiddelde waarde. De normale verdeling wordt ook wel een Gaussische verdeling genoemd, omdat deze is ontdekt door Carl Friedrich Gauss. Het wordt vaak de belcurve genoemd omdat de getallen zich zo uitspreiden dat ze de vorm van een bel op een grafiek hebben.
Getallen zijn niet normaal verdeeld als ze aan de ene of de andere kant van de gemiddelde waarde zijn gegroepeerd. Getallen kunnen verspreid zijn en toch normaal verdeeld zijn. De standaardafwijking geeft aan hoe sterk de getallen verdeeld zijn.

Donkerblauw is minder dan één standaardafwijking van het gemiddelde. Voor de normale verdeling omvat dit 68,27 procent van de getallen; terwijl twee standaardafwijkingen van het gemiddelde (middel- en donkerblauw) 95,45 procent omvatten; drie standaardafwijkingen (licht-, middel- en donkerblauw) 99,73 procent omvatten; en vier standaardafwijkingen 99,994 procent.
Verband tussen het gemiddelde en de standaardafwijking
Het gemiddelde (mean) en de standaardafwijking van een reeks gegevens worden meestal samen geschreven. Dan kan iemand begrijpen wat het gemiddelde getal is en hoe ver andere getallen in de groep zijn verspreid.
De spreiding van een groep getallen kan ook worden weergegeven door de variatiecoëfficiënt (CV), die de standaardafwijking gedeeld door het gemiddelde is. Het is een dimensieloos getal. Variatiecoëfficiënt wordt vaak vermenigvuldigd met 100% en geschreven als percentage.
Geschiedenis
De term standaardafwijking werd voor het eerst schriftelijk gebruikt door Karl Pearson in 1894, nadat hij deze in lezingen had gebruikt. Het was als vervanging van eerdere namen voor hetzelfde idee: Gauss gebruikte bijvoorbeeld gemiddelde fout.
Gerelateerde pagina's
- Nauwkeurigheid en precisie
- Steekproefgrootte
- Standaardfout
- Variantie
Vragen en antwoorden
V: Wat is standaardafwijking?
A: De standaardafwijking is een getal dat aangeeft hoe de metingen voor een groep zijn verspreid van het gemiddelde (gemiddelde of verwachte waarde).
V: Wat betekent een lage standaarddeviatie?
A: Een lage standaardafwijking betekent dat de meeste getallen dicht bij het gemiddelde liggen.
V: Wat betekent een hoge standaardafwijking?
A: Een hoge standaardafwijking betekent dat de getallen meer gespreid zijn.
V: Hoe wordt standaardafwijking in geld gebruikt?
A: In geld geeft de standaardafwijking van de verdiende rente aan hoe verschillend de verdiende rente van één persoon kan zijn van het gemiddelde.
V: Wanneer kan slechts een deel van een groep worden gemeten?
A: Vaak kan alleen een steekproef of een deel van een groep worden gemeten.
V: Hoe wordt de standaardafwijking van de hele groep weergegeven?
A: De standaardafwijking van de hele groep wordt weergegeven door de Griekse letter َ {Sigma}. .
V: Hoe wordt de standaarddeviatie van de steekproef weergegeven?
A: De standaardafwijking van de steekproef wordt weergegeven door s {displaystyle s} .
Zoek in de encyclopedie



