Chaostheorie: Uitleg, vlindereffect, voorbeelden en toepassingen
Ontdek chaostheorie, het vlindereffect, heldere voorbeelden en praktische toepassingen — begrijp hoe kleine veranderingen grote gevolgen hebben.
Chaostheorie is een tak van de wiskunde die zich bezighoudt met het gedrag van bepaalde dynamische systemen die extreem gevoelig zijn voor beginwaarden. Een heel kleine verandering in de starttoestand kan na verloop van tijd leiden tot een volledig ander verloop van het systeem. Dit maakt zulke systemen in de praktijk moeilijk of zelfs onmogelijk op lange termijn nauwkeurig te voorspellen, ondanks dat ze vaak deterministisch zijn (volgen vaste regels of formules).
Het vlindereffect en voorspelbaarheid
Een belangrijk en bekend begrip binnen de chaostheorie is het zogenaamde vlindereffect: het idee dat een kleine verstoring — metaforisch veroorzaakt door een vlinder — uiteindelijk invloed kan hebben op het weer of andere grote systemen. Daarom kunnen zelfs zeer krachtige computers, ook de grote computers het, vaak maar enkele dagen vooruit betrouwbare weersvoorspellingen leveren. Kleine meetfouten of onvolledige kennis van de begincondities groeien door de tijd heen uit tot grote afwijkingen.
Belangrijke begrippen hierbij zijn:
- Gevoeligheid voor beginwaarden (sensitivity to initial conditions): kleine verschillen in uitgangstoestand leiden tot exponentieel uiteenlopende uitkomsten.
- Lyapunov-exponent (in eenvoudige woorden): een maat voor hoe snel kleine fouten groeien; een positieve waarde wijst op chaos en beperkt de voorspelbare tijdshorizon.
- Deterministisch maar onvoorspelbaar: systemen kunnen volgens vaste wetten werken maar toch niet praktisch voorspelbaar zijn op lange termijn.
Patronen en attractoren
Sommige chaotische systemen lijken op het eerste gezicht willekeurig lijken, maar tonen vaak onderliggende structuren die niet volledig toevallig zijn. Deze structuren noemen we attractoren, en bij chaos vaak vreemde attractoren genoemd: geometrische, fractal-achtige patronen in de ruimtelijke weergave van de oplossingen. Een bekend voorbeeld uit de geschiedenis van de chaostheorie is de Lorenz-attractor, ontstaan uit eenvoudige vergelijkingen voor atmosferische convectie, die toch complexe, steeds wederkerende banen oplevert.
Voorbeelden van chaotisch gedrag
- Het weer en atmosferische stromingen — klassiek voorbeeld van een chaotisch systeem.
- Bevolkingsdynamica in ecologie (bijvoorbeeld schommelingen in populaties bij eenvoudige modelvergelijkingen zoals de logistieke kaart).
- Vloeistofstroming en turbulentie — overgang van ordelijk naar chaotisch gedrag in stromingen.
- Economische en financiële markten — sommige modellen laten chaotische bewegingen zien (hoewel echte markten ook door externe ruis worden beïnvloed).
- Biologische ritmes en hartritmestoornissen — chaos-theorie wordt gebruikt om onregelmatigheden in hart- en hersensignalen te analyseren.
Toepassingen
Hoewel chaos limitaties stelt aan lange termijnvoorspellingen, levert kennis uit de chaostheorie nuttige toepassingen op:
- Verbetering van weersmodellen en begrip van de grenzen van voorspelling — optimaal gebruik van voorspellingstijd en waarnemingen.
- Ontwerp van stabiliteits- en controlesystemen in techniek: herkennen van optreden van chaos en het terugbrengen naar gewenst gedrag (chaoscontrole).
- Medische diagnostiek: analyseren van onregelmatige signalen (bijvoorbeeld ECG) met methoden uit de chaos- en dynamische systeemtheorie.
- Veilige communicatie en cryptografie: gebruik van deterministische maar onvoorspelbare signalen voor versleuteling in sommige toepassingen.
- Ecologie en beheer: beter begrip van wanneer populaties plotseling kunnen omslaan en hoe kleine veranderingen groot effect kunnen hebben.
Quantumchaos
Quantumchaostheorie is een tak van de wetenschap die onderzoekt hoe klassieke chaotische eigenschappen zich vertalen of veranderen in de wereld van de kwantumfysica. Omdat kwantumsystemen andere regels en onzekerheden volgen, ontstaan nieuwe vragen over hoe begrip van chaos toepasbaar is op zeer kleine schalen.
Kort samengevat
- Chaostheorie bestudeert systemen die deterministisch kunnen zijn maar gevoelig voor kleine veranderingen, waardoor hun lange termijn-gedrag onvoorspelbaar wordt.
- Het vlindereffect illustreert hoe minuscule variaties aanzienlijk kunnen uitgroeien.
- Ondanks onvoorspelbaarheid biedt de theorie inzicht, meetmethoden en technieken die in veel praktische domeinen nuttig zijn.
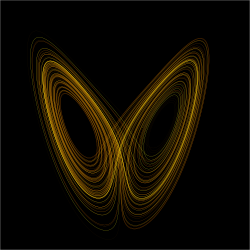
Een grafiek van een chaotische functie, de Lorenz attractor.

Als deze twee verbonden slingers in een positie zouden beginnen die ook maar een klein beetje anders zou zijn, zou de grijze lijn er heel anders uitzien.
Voorbeelden
Neem als voorbeeld een slinger die op een bepaald punt is bevestigd en vrij slingert. Door een tweede slinger aan de eerste te koppelen, wordt het systeem totaal anders. Het is heel moeilijk om weer in precies dezelfde positie te beginnen - een verandering in de uitgangspositie die zo klein is dat zij niet eens te zien is, kan er al snel toe leiden dat de slinger anders gaat slingeren dan hij eerst was.
Een zeer belangrijk onderdeel van de studie van de chaostheorie is de studie van wiskundige functies die bekend staan als fractals. Fractale functies werken als chaotische systemen: een kleine verandering in de beginwaarden kan de waarde van de functie veranderen op manieren die willekeurig lijken. Omdat ze wiskundig zijn, zijn ze gemakkelijk te bestuderen.
Verwante pagina's
- Discontinue functie
Vragen en antwoorden
V: Wat is de chaostheorie?
A: Chaostheorie is een tak van de wiskunde die systemen bestudeert die zeer gevoelig zijn, en een kleine verandering in het systeem kan ervoor zorgen dat het zich totaal anders gedraagt.
V: Waarom kunnen zelfs grote computers het weer niet nauwkeurig voorspellen?
A: Zelfs grote computers kunnen het weer niet voorspellen omdat de uitgangspositie van een chaotisch systeem, zoals het weer, zeer gevoelig is voor kleine veranderingen, en zelfs een kleine fout of verandering kan de voorspelling volledig verkeerd maken.
V: Wat is het "vlindereffect"?
A: Het "vlindereffect" is een begrip in de chaostheorie dat verwijst naar het idee dat zelfs kleine veranderingen, zoals het flapperen van de vleugels van een vlinder, een grote invloed kunnen hebben op een chaotisch systeem, zoals het weer.
V: Zijn er systemen die willekeurig lijken, maar dat eigenlijk niet zijn?
A: Ja, de chaostheorie suggereert dat sommige systemen of patronen op het eerste gezicht willekeurig lijken, maar dat niet zijn, en dat zorgvuldige observatie de chaotische patronen kan onthullen.
V: Wat is het hoofdidee van de chaostheorie?
A: Het hoofdidee van de chaostheorie is dat een klein verschil in de uitgangspositie van een proces een significante verandering in de tijd kan teweegbrengen.
V: Wat is de kwantumchaostheorie?
A: De kwantumchaostheorie is een nieuw idee in de studie van de chaostheorie dat de principes ervan toepast op de kwantumfysica.
V: Hoe beïnvloeden zeer kleine veranderingen chaotische systemen?
A: Zeer kleine veranderingen in de uitgangspositie van een chaotisch systeem kunnen een aanzienlijk verschil maken in het gedrag ervan in de loop der tijd. Dit komt omdat chaotische systemen zeer gevoelig zijn en kleine veranderingen kunnen leiden tot grote verschillen in hun gedrag.
Zoek in de encyclopedie