Kwantummechanica
De kwantummechanica verklaart hoe het universum werkt op een schaal die kleiner is dan atomen. Het wordt ook wel kwantumfysica of kwantumtheorie genoemd. Mechanica is het deel van de natuurkunde dat verklaart hoe dingen bewegen, en kwantum is het Latijnse woord voor "hoeveel". Een kwantum van energie is de kleinst mogelijke hoeveelheid (of de minst extra hoeveelheid), en de kwantummechanica beschrijft hoe die energie beweegt of op elkaar inwerkt.
Atomen werden lang beschouwd als de kleinste stukjes materie, maar de moderne wetenschap heeft aangetoond dat er nog kleinere subatomaire deeltjes bestaan, zoals protonen, neutronen en elektronen. De kwantummechanica beschrijft hoe de deeltjes waaruit atomen bestaan, werken.
De kwantummechanica vertelt ons ook hoe elektromagnetische golven (zoals licht) werken. Golf-deeltjes dualiteit betekent dat deeltjes zich gedragen als golven en golven zich gedragen als deeltjes. (Het zijn geen twee soorten dingen, ze lijken op beide: dit is hun dualiteit). Veel van de moderne natuur- en scheikunde kan worden beschreven en begrepen met behulp van de wiskundige regels van de kwantummechanica.
De wiskunde die wordt gebruikt om subatomaire deeltjes en elektromagnetische golven te bestuderen, is zeer complex omdat zij zich op zeer vreemde manieren gedragen.
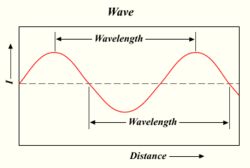
De golflengte van een lichtgolf
Golven en fotonen
Fotonen zijn deeltjes ter grootte van een punt, kleiner dan atomen. Fotonen zijn als "pakketjes" of pakketjes energie. Lichtbronnen zoals kaarsen of lasers produceren licht in stukjes die fotonen worden genoemd.
Hoe meer fotonen een lamp produceert, hoe feller het licht. Licht is een vorm van energie die zich gedraagt als de golven in water of radiogolven. De afstand tussen de top van de ene golf en de top van de volgende golf wordt een 'golflengte' genoemd. Elk foton draagt een bepaalde hoeveelheid, of 'kwantum', energie met zich mee, afhankelijk van de golflengte.
De kleur van licht hangt af van de golflengte. De kleur violet (de onderste of binnenste kleur van de regenboog) heeft een golflengte van ongeveer 400 nm ("nanometer"), ofwel 0,00004 centimeter. Fotonen met een golflengte van 10-400 nm worden ultraviolet (of UV) licht genoemd. Dit licht kan niet worden gezien door het menselijk oog. Aan de andere kant van het spectrum is rood licht ongeveer 700 nm. Infrarood licht is ongeveer 700 nm tot 300.000 nm. Menselijke ogen zijn ook niet gevoelig voor infrarood licht.
Golflengten zijn niet altijd zo klein. Radiogolven hebben langere golflengten. De golflengte van een FM-radio kan enkele meters lang zijn (stations die uitzenden op 99.5 FM zenden bijvoorbeeld radio-energie uit met een golflengte van ongeveer 3 meter, dat is ongeveer 10 voet). Elk foton heeft een bepaalde hoeveelheid energie die gerelateerd is aan zijn golflengte. Hoe korter de golflengte van een foton, hoe groter zijn energie. Een ultraviolet foton heeft bijvoorbeeld meer energie dan een infrarood foton.
Golflengte en frequentie (het aantal keren dat de golf per seconde opkomt) zijn omgekeerd evenredig, wat betekent dat een langere golflengte een lagere frequentie heeft, en omgekeerd. Als de kleur van het licht infrarood is (lager in frequentie dan rood licht), kan elk foton verwarmen wat het raakt. Dus als een sterke infraroodlamp (een warmtelamp) op een persoon wordt gericht, zal die persoon warm of zelfs heet aanvoelen, vanwege de energie die in de vele fotonen is opgeslagen. Het oppervlak van de infraroodlamp kan zelfs heet genoeg worden om iemand die hem aanraakt te verbranden. Mensen kunnen geen infrarood licht zien, maar we kunnen de straling wel voelen in de vorm van warmte. Iemand die bijvoorbeeld langs een stenen gebouw loopt dat door de zon is verwarmd, voelt de warmte van het gebouw zonder dat hij het hoeft aan te raken.
De wiskundige vergelijkingen van de kwantummechanica zijn abstract, wat betekent dat het onmogelijk is om de exacte fysische eigenschappen van een deeltje (zoals zijn positie of momentum) met zekerheid te kennen. In plaats daarvan geeft een wiskundige functie, de golffunctie genaamd, informatie over de waarschijnlijkheid waarmee een deeltje een bepaalde eigenschap heeft. De golffunctie kan u bijvoorbeeld vertellen wat de waarschijnlijkheid is dat een deeltje zich op een bepaalde plaats bevindt, maar kan u niet met zekerheid zeggen waar het zich bevindt. Vanwege deze onzekerheid en andere factoren kunt u de klassieke mechanica (de natuurkunde die beschrijft hoe grote voorwerpen bewegen) niet gebruiken om de beweging van kwantumdeeltjes te voorspellen.
Ultraviolet licht heeft een hogere frequentie dan violet licht, zodat het niet eens in het zichtbare lichtbereik valt. Elk foton in het ultraviolette bereik heeft veel energie, genoeg om de huidcellen te beschadigen en zonnebrand te veroorzaken. In feite worden de meeste vormen van zonnebrand niet veroorzaakt door warmte, maar door de hoge energie van de UV-stralen van de zon die uw huidcellen beschadigen. Nog hogere frequenties van licht (of elektromagnetische straling) kunnen dieper in het lichaam doordringen en nog meer schade veroorzaken. Röntgenstralen hebben zoveel energie dat ze diep in het menselijk lichaam kunnen doordringen en cellen kunnen doden. Mensen kunnen ultraviolet licht of röntgenstraling niet zien of voelen. Zij weten alleen dat zij onder zulk hoogfrequent licht zijn geweest wanneer zij een stralingsbrandwond oplopen. Op plaatsen waar het belangrijk is ziektekiemen te doden, worden vaak ultraviolette lampen gebruikt om bacteriën, schimmels, enz. te vernietigen. Röntgenstralen worden soms gebruikt om kankercellen te doden.
De kwantummechanica begon toen men ontdekte dat als een deeltje een bepaalde frequentie heeft, het ook een bepaalde hoeveelheid energie moet hebben. Energie is evenredig met frequentie (E ∝ f). Hoe hoger de frequentie, hoe meer energie een foton heeft, en hoe meer schade het kan aanrichten. De kwantummechanica groeide later uit om de interne structuur van atomen te verklaren. De kwantummechanica verklaart ook de manier waarop een foton met zichzelf kan interfereren, en vele andere dingen die in de klassieke natuurkunde nooit voor mogelijk werden gehouden.
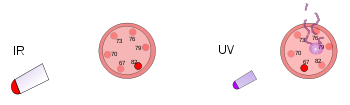
Links ligt een plastic thermometer onder een felle warmtelamp. Deze infrarode straling verwarmt de thermometer, maar beschadigt hem niet. Rechts wordt een andere plastic thermometer geraakt door ultraviolet licht met een lage intensiteit. Deze straling beschadigt de thermometer, maar verwarmt hem niet.

Zwart links is ultraviolet (hoge frequentie); zwart rechts is infrarood (lage frequentie).
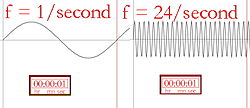
Pictografische beschrijving van de frequentie
Kwantisering
Max Planck ontdekte het verband tussen frequentie en energie. Niemand eerder had ooit gedacht dat frequentie recht evenredig is met energie (dit betekent dat als het ene verdubbelt, het andere dat ook doet). Onder de zogenaamde natuurlijke eenheden zou het getal dat de frequentie van een foton weergeeft, ook de energie ervan weergeven. De vergelijking zou dan zijn:
wat betekent dat energie gelijk is aan frequentie.
Maar zoals de natuurkunde zich ontwikkelde, was er geen natuurlijk verband tussen de eenheden die werden gebruikt om energie te meten en de eenheden die gewoonlijk werden gebruikt om tijd (en dus frequentie) te meten. Dus de formule die Planck uitwerkte om alle getallen goed te krijgen was:
of, energie is gelijk aan h maal frequentie. Deze h is een getal dat de constante van Planck wordt genoemd, naar zijn ontdekker.
De kwantummechanica is gebaseerd op de wetenschap dat een foton van een bepaalde frequentie een foton van een bepaalde hoeveelheid energie betekent. Naast die relatie kan een bepaald soort atoom alleen bepaalde frequenties van straling afgeven, dus kan het ook alleen fotonen afgeven die bepaalde hoeveelheden energie hebben.
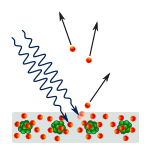
Foto-elektrisch effect: fotonen raken metaal en elektronen worden weggedrukt.
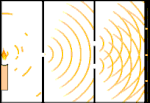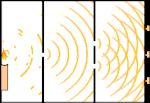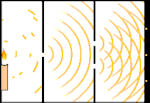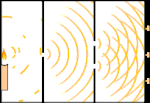
Dubbele spleet experiment: licht gaat van de lichtbron links naar franjes (gemarkeerd in de zwarte rand) rechts.
Geschiedenis
Isaac Newton dacht dat licht bestond uit zeer kleine dingen die wij nu deeltjes zouden noemen (hij noemde ze "Corpuscles"). Christiaan Huygens dacht dat licht uit golven bestond. Wetenschappers dachten dat iets niet tegelijkertijd een deeltje en een golf kan zijn.
Wetenschappers deden experimenten om erachter te komen of licht uit deeltjes of uit golven bestond. Zij ontdekten dat beide ideeën klopten - licht bestond op de een of andere manier uit zowel golven als deeltjes. Het Double-slit experiment van Thomas Young toonde aan dat licht zich als een golf moest gedragen. Het door Albert Einstein ontdekte foto-elektrisch effect bewees dat licht zich moest gedragen als deeltjes die specifieke hoeveelheden energie droegen, en dat de energieën gekoppeld waren aan hun frequenties. Dit experimentele resultaat wordt in de kwantummechanica de "golf-deeltjes dualiteit" genoemd. Later ontdekten natuurkundigen dat alles zich zowel als golf als als deeltje gedraagt, niet alleen licht. Dit effect is echter veel kleiner bij grote objecten.
Hier zijn enkele van de mensen die de basisonderdelen van de kwantummechanica hebben ontdekt: Max Planck, Albert Einstein, Satyendra Nath Bose, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, John von Neumann en Richard Feynman. Zij deden hun werk in de eerste helft van de 20e eeuw.

Van links naar rechts: Max Planck, Albert Einstein, Niels Bohr, Louis de Broglie, Max Born, Paul Dirac, Werner Heisenberg, Wolfgang Pauli, Erwin Schrödinger, Richard Feynman.
Voorbij Planck
De formules en ideeën van de kwantummechanica werden gemaakt om het licht te verklaren dat afkomstig is van gloeiend waterstof. De kwantumtheorie van het atoom moest ook verklaren waarom het elektron in zijn baan blijft, wat andere ideeën niet konden verklaren. Uit de oudere ideeën volgde dat het elektron in het centrum van het atoom zou moeten vallen omdat het aanvankelijk door zijn eigen energie in zijn baan wordt gehouden, maar het zou snel zijn energie verliezen wanneer het in zijn baan draait. (Dit is omdat de elektronen en andere geladen deeltjes gekend waren om licht uit te zenden en energie te verliezen wanneer zij snelheid veranderden of draaiden.)
Waterstoflampen werken als neonlampen, maar neonlampen hebben hun eigen unieke groep kleuren (en frequenties) van licht. Wetenschappers ontdekten dat zij alle elementen konden identificeren aan de hand van de lichtkleuren die zij produceren. Zij konden alleen niet achterhalen hoe de frequenties werden bepaald.
Toen bedacht de Zwitserse wiskundige Johann Balmer een vergelijking die aangaf wat λ (lambda, voor golflengte) zou zijn:
waarbij B een getal is dat Balmer heeft vastgesteld op 364,56 nm.
Deze vergelijking werkte alleen voor het zichtbare licht van een waterstoflamp. Maar later werd de vergelijking algemener gemaakt:
waarbij R de Rydberg-constante is, gelijk aan 0,0110 nm−1 , en n groter moet zijn dan m.
Door verschillende getallen in te voeren voor m en n, kunnen gemakkelijk frequenties worden voorspeld voor vele soorten licht (ultraviolet, zichtbaar en infrarood). Om te zien hoe dit werkt, gaat u naar Hyperphysics en gaat u voorbij het midden van de pagina naar beneden. (Gebruik H = 1 voor waterstof.)
In 1908 maakte Walter Ritz het Ritz-combinatieprincipe dat laat zien hoe bepaalde hiaten tussen frequenties zich blijven herhalen. Dit bleek enkele jaren later belangrijk voor Werner Heisenberg.
In 1905 gebruikte Albert Einstein het idee van Planck om aan te tonen dat een lichtstraal bestaat uit een stroom deeltjes die fotonen worden genoemd. De energie van elk foton hangt af van zijn frequentie. Einsteins idee is het begin van het idee in de kwantummechanica dat alle subatomaire deeltjes zoals elektronen, protonen, neutronen en andere tegelijkertijd golven en deeltjes zijn. (Zie de afbeelding van het atoom met het elektron als golven bij het atoom.) Dit leidde tot een theorie over subatomaire deeltjes en elektromagnetische golven die golf-deeltjes dualiteit wordt genoemd. Hierbij waren deeltjes en golven noch het een noch het ander, maar hadden ze bepaalde eigenschappen van beide.
In 1913 kwam Niels Bohr met het idee dat elektronen alleen bepaalde banen rond de kern van een atoom konden aannemen. Volgens de theorie van Bohr zouden de getallen m en n in bovenstaande vergelijking banen kunnen voorstellen. Volgens de theorie van Bohr kunnen elektronen beginnen in een baan m en eindigen in een baan n, of een elektron kan beginnen in een baan n en eindigen in een baan m, dus als een foton een elektron raakt, wordt de energie ervan geabsorbeerd en gaat het elektron vanwege die extra energie naar een hogere baan. Volgens de theorie van Bohr, als een elektron van een hogere baan naar een lagere baan valt, zal het energie moeten afstaan in de vorm van een foton. De energie van het foton zal gelijk zijn aan het energieverschil tussen de twee banen, en de energie van een foton zorgt ervoor dat het een bepaalde frequentie en kleur heeft. De theorie van Bohr bood een goede verklaring voor veel aspecten van subatomaire verschijnselen, maar gaf geen antwoord op de vraag waarom elk van de kleuren licht die worden geproduceerd door gloeiend waterstof (en door gloeiend neon of een ander element) een eigen helderheid heeft, en de verschillen in helderheid altijd hetzelfde zijn voor elk element.
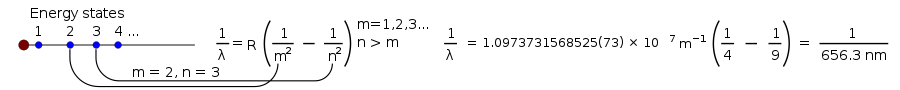
Tegen de tijd dat Niels Bohr met zijn theorie kwam, waren de meeste dingen over het door een waterstoflamp geproduceerde licht bekend, maar wetenschappers konden de helderheid van elk van de door gloeiende waterstof geproduceerde lijnen nog steeds niet verklaren.
Werner Heisenberg nam de taak op zich om de helderheid of "intensiteit" van elke lijn te verklaren. Hij kon geen eenvoudige regel gebruiken zoals die welke Balmer had bedacht. Hij moest de zeer moeilijke wiskunde van de klassieke natuurkunde gebruiken, die alles uitrekent in termen van dingen als de massa (gewicht) van een elektron, de lading (statische elektrische kracht) van een elektron, en andere kleine hoeveelheden. De klassieke natuurkunde had al antwoorden voor de helderheid van de kleurenbanden die een waterstoflamp produceert, maar de klassieke theorie zei dat er een continue regenboog moest zijn, en niet vier afzonderlijke kleurenbanden. De verklaring van Heisenberg luidt:
Er bestaat een wet die zegt welke lichtfrequenties gloeiend waterstof produceert. De wet moet uit elkaar liggende frequenties voorspellen wanneer de betrokken elektronen tussen banen dicht bij de kern (centrum) van het atoom bewegen, maar hij moet ook voorspellen dat de frequenties steeds dichter bij elkaar komen te liggen naarmate we kijken naar wat het elektron doet wanneer het verder en verder naar buiten beweegt tussen banen. Zij zal ook voorspellen dat de intensiteitsverschillen tussen de frequenties steeds dichter bij elkaar komen te liggen naarmate we verder naar buiten gaan. Waar de klassieke fysica al de juiste antwoorden geeft met één reeks vergelijkingen, moet de nieuwe fysica dezelfde antwoorden geven, maar met andere vergelijkingen.
De klassieke natuurkunde gebruikt de wiskundige methoden van Joseph Fourier om een wiskundig beeld te maken van de fysieke wereld, Het gebruikt verzamelingen gladde krommen die samengaan om één gladde kromme te maken die, in dit geval, intensiteiten geeft voor licht van alle frequenties van wat licht. Maar het klopt niet, want die gladde curve verschijnt alleen bij hogere frequenties. Bij lagere frequenties zijn er altijd geïsoleerde punten en verbindt niets de punten. Dus, om een kaart van de echte wereld te maken, moest Heisenberg een grote verandering aanbrengen. Hij moest iets doen om alleen de getallen eruit te pikken die overeenkwamen met wat men in de natuur zag. Soms zegt men dat hij deze vergelijkingen "gokte", maar hij deed geen blinde gok. Hij vond wat hij nodig had. De getallen die hij berekende zouden stippen op een grafiek zetten, maar er zou geen lijn getrokken worden tussen de stippen. En het maken van een "grafiek" van punten voor elke reeks berekeningen zou veel papier hebben verspild en niets hebben opgeleverd. Heisenberg vond een manier om de intensiteiten voor verschillende frequenties efficiënt te voorspellen en die informatie op een nuttige manier te organiseren.
Door gewoon de hierboven gegeven empirische regel te gebruiken, de regel waarmee Balmer begon en die Rydberg verbeterde, kunnen we zien hoe we een reeks getallen kunnen krijgen die Heisenberg zouden helpen het soort beeld te krijgen dat hij wilde:
De regel zegt dat wanneer het elektron van de ene baan naar de andere gaat, het energie wint of verliest, afhankelijk van de vraag of het verder van het centrum of dichterbij komt. Wij kunnen deze banen of energieniveaus dus plaatsen als kopjes langs de bovenkant en de zijkant van een rooster. Om historische redenen wordt de laagste baan n genoemd, en de volgende baan wordt n - a genoemd, dan komt n - b, enzovoort. Het is verwarrend dat men negatieve getallen gebruikte terwijl de elektronen juist energie wonnen, maar zo is het nu eenmaal.
Aangezien de Rydberg-regel ons frequenties geeft, kunnen we die regel gebruiken om getallen in te voeren, afhankelijk van waar het elektron naartoe gaat. Als het elektron begint bij n en eindigt bij n, dan is het nergens naartoe gegaan, dus heeft het geen energie gewonnen en geen energie verloren. De frequentie is dus 0. Als het elektron begint bij n-a en eindigt bij n, dan is het van een hogere baan naar een lagere baan gedaald. Dan verliest het energie, en de energie die het verliest wordt zichtbaar als een foton. Het foton heeft een bepaalde hoeveelheid energie, e, en die is gerelateerd aan een bepaalde frequentie f door de vergelijking e = h f. We weten dus dat een bepaalde verandering van baan een bepaalde lichtfrequentie, f, oplevert. Als het elektron begint bij n en eindigt bij n - a, betekent dit dat het van een lagere baan naar een hogere baan is gegaan. Dat gebeurt alleen wanneer een foton met een bepaalde frequentie en energie van buitenaf komt, door het elektron wordt geabsorbeerd en het zijn energie geeft, en dat zorgt ervoor dat het elektron naar een hogere baan gaat. Dus, om alles logisch te houden, schrijven we die frequentie als een negatief getal. Er was een foton met een bepaalde frequentie en die is nu weggenomen.
We kunnen dus een rooster als dit maken, waarbij f(a←b) de frequentie betekent die optreedt wanneer een elektron van energietoestand (baan) b naar energietoestand a gaat (Nogmaals, de reeksen zien er achterstevoren uit, maar zo werden ze oorspronkelijk geschreven):
Raster van f
| Elektronenstaten | n | n-a | n-b | n-c | .... | |
| n | f(n←n) | f(n←n-a) | f(n←n-b) | f(n←n-c) | ..... | |
| n-a | f(n-a←n) | f(n-a←n-a) | f(n-a←n-b) | f(n-a←n-c) | ..... | |
| n-b | f(n-b←n) | f(n-b←n-a) | f(n-b←n-b) | f(n-b←n-c) | ..... | |
| transitie.... | ..... | ..... | ..... | ..... |
Heisenberg heeft de roosters niet zo gemaakt. Hij deed alleen de wiskunde waarmee hij de intensiteiten kreeg die hij zocht. Maar daarvoor moest hij twee amplitudes (de hoogte van een golf) met elkaar vermenigvuldigen om de intensiteit te berekenen. (In de klassieke natuurkunde is intensiteit gelijk aan amplitude in het kwadraat.) Hij maakte een vreemde vergelijking om dit probleem op te lossen, schreef de rest van zijn artikel uit, overhandigde het aan zijn baas en ging op vakantie. Dr. Born keek naar zijn grappige vergelijking en het leek een beetje gek. Hij moet zich hebben afgevraagd: "Waarom heeft Heisenberg mij dit rare ding gegeven? Waarom moet hij het zo doen?" Toen realiseerde hij zich dat hij keek naar een blauwdruk voor iets dat hij al heel goed kende. Hij was gewend om het rooster of de tabel die we konden schrijven door bijvoorbeeld alle wiskunde voor frequenties te doen, een matrix te noemen. En de vreemde vergelijking van Heisenberg was een regel om twee van die matrices met elkaar te vermenigvuldigen. Max Born was een zeer, zeer goede wiskundige. Hij wist dat, aangezien de twee matrices (rasters) die met elkaar werden vermenigvuldigd verschillende dingen vertegenwoordigden (zoals positie (x,y,z) en momentum (mv), bijvoorbeeld), je bij vermenigvuldiging van de eerste matrix met de tweede een antwoord kreeg en bij vermenigvuldiging van de tweede matrix met de eerste matrix een ander antwoord. Ook al had hij geen verstand van matrixwiskunde, Heisenberg zag dit "verschillende antwoorden" probleem al en hij had er last van. Maar Dr. Born was zo'n goede wiskundige dat hij zag dat het verschil tussen de eerste matrixvermenigvuldiging en de tweede matrixvermenigvuldiging altijd te maken had met de constante van Planck, h, vermenigvuldigd met de vierkantswortel van negatief één, i. Dus binnen een paar dagen na Heisenbergs ontdekking hadden ze al de basiswiskunde voor wat Heisenberg graag het "onbepaaldheidsprincipe" noemde. Met "onbepaaldheid" bedoelde Heisenberg dat iets als een elektron niet vastligt totdat het vastligt. Het is een beetje als een kwal die altijd rondkruipt en niet "op één plaats" kan zijn tenzij je hem doodt. Later kregen mensen de gewoonte om het "Heisenbergs onzekerheidsprincipe" te noemen, waardoor veel mensen de fout maakten te denken dat elektronen en dat soort dingen echt "ergens" zijn, maar dat we er alleen in ons eigen hoofd onzeker over zijn. Dat idee is verkeerd. Het is niet waar Heisenberg het over had. Moeite hebben met het meten van iets is een probleem, maar het is niet het probleem waar Heisenberg het over had.
Heisenbergs idee is erg moeilijk te begrijpen, maar we kunnen het duidelijker maken met een voorbeeld. Eerst zullen we deze rasters "matrices" gaan noemen, omdat we het straks over matrixvermenigvuldiging moeten hebben.
Stel dat we beginnen met twee soorten metingen, positie (q) en momentum (p). In 1925 schreef Heisenberg een vergelijking als deze:

Hij wist het niet, maar deze vergelijking geeft een blauwdruk voor het uitschrijven van twee matrices (roosters) en het vermenigvuldigen ervan. De regels voor het vermenigvuldigen van de ene matrix met de andere zijn een beetje rommelig, maar hier zijn de twee matrices volgens de blauwdruk, en dan hun product:
Matrix van p
| Elektronenstaten | n-a | n-b | n-c | .... | |
| n | p(n←n-a) | p(n←n-b) | p(n←n-c) | ..... | |
| n-a | p(n-a←n-a) | p(n-a←n-b) | p(n-a←n-c) | ..... | |
| n-b | p(n-b←n-a) | p(n-b←n-b) | p(n-b←n-c) | ..... | |
| transitie.... | ..... | ..... | ..... | ..... |
Matrix van q
| Elektronenstaten | n-b | n-c | n-d | .... | |
| n-a | q(n-a←n-b) | q(n-a←n-c) | q(n-a←n-d) | ..... | |
| n-b | q(n-b←n-b) | q(n-b←n-c) | q(n-b←n-d) | ..... | |
| n-c | q(n-c←n-b) | q(n-c←n-c) | q(n-c←n-d) | ..... | |
| transitie.... | ..... | ..... | ..... | ..... |
De matrix voor het product van de bovenstaande twee matrices zoals gespecificeerd door de relevante vergelijking in Heisenberg's 1925 paper is:
| Elektronenstaten | n-b | n-c | n-d | ..... |
| n | A | ..... | ..... | ..... |
| n-a | ..... | B | ..... | ..... |
| n-b | ..... | ..... | C | ..... |
Waar:
A=p(n←n-a)*q(n-a←n-b)+p(n←n-b)*q(n-b←n-b)+p(n←n-c)*q(n-c←n-b)+.....
B=p(n-a←n-a)*q(n-a←n-c)+p(n-a←n-b)*q(n-b←n-c)+p(n-a←n-c)*q(n-c←n-c)+.....
C=p(n-b←n-a)*q(n-a←n-d)+p(n-b←n-b)*q(n-b←n-d)+p(n-b←n-c)*q(n-d←n-d)+.....
enzovoort.
Als de matrices zouden worden omgekeerd, zou dit de volgende waarden opleveren:
A=q(n←n-a)*p(n-a←n-b)+q(n←n-b)*p(n-b←n-b)+q(n←n-c)*p(n-c←n-b)+.....
B=q(n-a←n-a)*p(n-a←n-c)+q(n-a←n-b)*p(n-b←n-c)+q(n-a←n-c)*p(n-c←n-c)+.....
C=q(n-b←n-a)*p(n-a←n-d)+q(n-b←n-b)*p(n-b←n-d)+q(n-b←n-c)*p(n-d←n-d)+.....
enzovoort.
Merk op hoe het veranderen van de volgorde van vermenigvuldiging stap voor stap de getallen verandert die daadwerkelijk worden vermenigvuldigd.

Zichtbaar licht van gloeiende waterstof. (Golflengten in nanometer.)
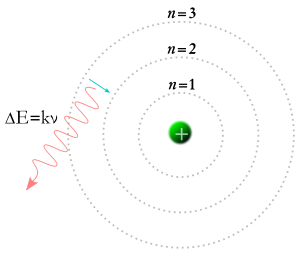
Een elektron valt in een lagere baan en er ontstaat een foton.
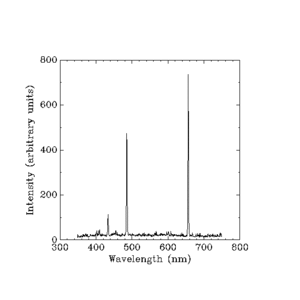
Uitgespreide intensiteiten in willekeurige eenheden
Voorbij Heisenberg
Het werk van Werner Heisenberg leek een impasse te doorbreken. Al snel kwamen er vele andere manieren om dingen te verklaren van mensen als Louis de Broglie, Max Born, Paul Dirac, Wolfgang Pauli en Erwin Schrödinger. Het werk van elk van deze natuurkundigen is zijn eigen verhaal. De wiskunde van Heisenberg en eerdere mensen is niet erg moeilijk te begrijpen, maar de vergelijkingen werden al snel erg ingewikkeld naarmate natuurkundigen zich meer verdiepten in de atomaire wereld.
Verdere mysteries
In de begindagen van de kwantummechanica suggereerde Albert Einstein dat als de kwantummechanica juist was, er sprake zou zijn van "spooky action at a distance". Het bleek dat de kwantummechanica gelijk had, en dat wat Einstein had gebruikt als reden om de kwantummechanica te verwerpen ook echt gebeurde. Dit soort "spookachtige verbinding" tussen bepaalde kwantumgebeurtenissen wordt nu "kwantumverstrengeling" genoemd.
Wanneer een experiment twee dingen (fotonen, elektronen, enz.) samenbrengt, moeten zij een gemeenschappelijke beschrijving in de kwantummechanica delen. Wanneer zij later worden gescheiden, behouden zij dezelfde kwantummechanische beschrijving of "toestand". In het diagram is de ene eigenschap (bv. "opwaartse" spin) in rood getekend, en de andere (bv. "neerwaartse" spin) in blauw. De paarse band betekent dat wanneer bijvoorbeeld twee elektronen worden samengevoegd, het paar beide eigenschappen deelt. Beide elektronen kunnen dus zowel up spin als down spin vertonen. Als ze later worden gescheiden, waarbij één op aarde blijft en één naar een planeet van de ster Alpha Centauri gaat, hebben ze nog steeds beide spins. Met andere woorden, elk van hen kan "besluiten" om zich te tonen als een spin-up elektron of een spin-down elektron. Maar als iemand later de andere meet, moet deze "besluiten" om de tegengestelde spin aan te tonen.
Einstein betoogde dat het over zo'n grote afstand te gek was om te denken dat het dwingen van één elektron om zijn spin te tonen er op de een of andere manier voor zou zorgen dat het andere elektron een tegenovergestelde eigenschap zou vertonen. Hij zei dat de twee elektronen altijd al spin-up of spin-down moeten zijn geweest, maar dat de kwantummechanica niet kon voorspellen welke eigenschap elk elektron had. Het niet kunnen voorspellen, slechts het kunnen bekijken van één van hen met het juiste experiment, betekende dat de kwantummechanica iets belangrijks niet kon verklaren. Daarom, zei Einstein, had de kwantummechanica een groot gat. De kwantummechanica was onvolledig.
Later bleek uit experimenten dat Einstein het bij het verkeerde eind had.
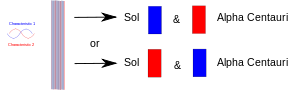
Twee verstrengelde deeltjes worden gescheiden: één op aarde en één meegenomen naar een verre planeet. Door een van hen te meten moet het "beslissen" welke rol het aanneemt, en het andere moet dan de andere rol aannemen telkens wanneer (daarna) het wordt gemeten.
Heisenberg onzekerheidsprincipe
In 1925 beschreef Werner Heisenberg het Onzekerheidsprincipe, dat zegt dat hoe meer we weten over waar een deeltje zich bevindt, hoe minder we kunnen weten over hoe snel het gaat en in welke richting. Met andere woorden, hoe meer we weten over de snelheid en de richting van iets kleins, hoe minder we kunnen weten over de positie ervan. Natuurkundigen hebben het in dergelijke discussies meestal over het momentum in plaats van over de snelheid. Momentum is gewoon de snelheid van iets in een bepaalde richting maal zijn massa.
De reden achter het onzekerheidsprincipe van Heisenberg zegt dat we nooit zowel de plaats als het momentum van een deeltje kunnen kennen. Omdat licht een overvloedig deeltje is, wordt het gebruikt om andere deeltjes te meten. De enige manier om het te meten is de lichtgolf af te kaatsen op het deeltje en de resultaten te registreren. Als een lichtstraal met hoge energie, of hoge frequentie, wordt gebruikt, kunnen we precies zeggen waar het zich bevindt, maar niet hoe snel het ging. Dit komt doordat het foton met hoge energie energie overdraagt op het deeltje en de snelheid van het deeltje verandert. Als we een foton met lage energie gebruiken, kunnen we zeggen hoe snel het gaat, maar niet waar het is. Dat komt omdat wij licht met een langere golflengte gebruiken. De langere golflengte betekent dat het deeltje zich overal langs het traject van de golf kan bevinden.
Het principe zegt ook dat er veel meetparen zijn waarvan we niet beide kunnen weten over een deeltje (een heel klein ding), hoe hard we ook proberen. Hoe meer we te weten komen over één van zo'n paar, hoe minder we kunnen weten over het andere.
Zelfs Albert Einstein had moeite met zo'n bizar concept en zei in een bekend debat: "God dobbelt niet". Hierop antwoordde de Deense natuurkundige Niels Bohr beroemd: "Einstein, vertel God niet wat hij moet doen".
Toepassingen van kwantummechanica
Elektronen omringen de kern van elk atoom. Chemische bindingen verbinden atomen tot moleculen. Een chemische binding verbindt twee atomen wanneer elektronen tussen die atomen worden gedeeld. Kwantummechanica is dus de fysica van de chemische binding en van de chemie. Kwantummechanica helpt ons te begrijpen hoe moleculen worden gemaakt, en wat hun eigenschappen zijn.
Kwantummechanica kan ons ook helpen grote dingen te begrijpen, zoals sterren en zelfs het hele heelal. Kwantummechanica is een zeer belangrijk onderdeel van de theorie over hoe het heelal begon, de zogenaamde oerknal.
Alles van materie wordt aangetrokken door andere materie vanwege een fundamentele kracht die zwaartekracht heet. Einsteins theorie die de zwaartekracht verklaart, heet de algemene relativiteitstheorie. Een probleem in de moderne natuurkunde is dat sommige conclusies van de kwantummechanica niet lijken overeen te komen met de algemene relativiteitstheorie.
Kwantummechanica is het deel van de natuurkunde dat kan verklaren waarom alle elektronische technologie werkt zoals ze werkt. Zo verklaart de kwantummechanica hoe computers werken, omdat computers elektronische machines zijn. Maar de ontwerpers van de vroege computerhardware van rond 1950 of 1960 hoefden niet na te denken over kwantummechanica. De ontwerpers van radio's en televisies in die tijd dachten ook niet na over kwantummechanica. Voor het ontwerp van de krachtigere geïntegreerde schakelingen en computergeheugentechnologieën van de laatste jaren is echter wel kwantummechanica nodig.
Kwantummechanica heeft ook technologieën mogelijk gemaakt zoals:
Waarom kwantummechanica moeilijk te leren is
Kwantummechanica is om verschillende redenen een uitdagend onderwerp:
- Kwantummechanica verklaart dingen op heel andere manieren dan wat wij als kind over de wereld leren.
- Voor het begrijpen van kwantummechanica is meer wiskunde nodig dan algebra en eenvoudige calculus. Het vereist ook matrixalgebra, complexe getallen, kansrekening en partiële differentiaalvergelijkingen.
- Natuurkundigen weten niet zeker wat sommige vergelijkingen van de kwantummechanica ons vertellen over de echte wereld.
- Kwantummechanica suggereert dat atomen en subatomaire deeltjes zich op vreemde manieren gedragen, totaal anders dan alles wat wij in ons dagelijks leven zien.
- Kwantummechanica beschrijft dingen die extreem klein zijn, zodat we sommige ervan niet kunnen zien zonder speciale apparatuur, en veel ervan helemaal niet kunnen zien.
De kwantummechanica beschrijft de natuur op een andere manier dan wij gewoonlijk over wetenschap denken. Het vertelt ons hoe waarschijnlijk het is dat sommige dingen zullen gebeuren, in plaats van ons te vertellen dat ze zeker zullen gebeuren.
Een voorbeeld is het dubbelspletenexperiment van Young. Als we afzonderlijke fotonen (afzonderlijke eenheden licht) van een laser op een vel fotografische film schieten, zien we een enkele lichtvlek op de ontwikkelde film. Als we een metalen plaat ertussen leggen en twee zeer smalle spleten in de plaat maken, en we vuren veel fotonen op de metalen plaat, en die moeten door de spleten, dan zien we iets opmerkelijks. Over het hele vel ontwikkelde film zien we een reeks heldere en donkere banden. Wij kunnen met behulp van wiskunde precies vertellen waar de heldere banden zullen zijn en hoe helder het licht was dat ze maakte, dat wil zeggen, wij kunnen van tevoren vertellen hoeveel fotonen op elke band zullen vallen. Maar als we het proces vertragen en kijken waar elk foton op het scherm terechtkomt, kunnen we nooit van tevoren zeggen waar het volgende foton zal opduiken. Wij weten wel zeker dat de kans het grootst is dat een foton op de middelste heldere band terechtkomt, en dat de kans steeds kleiner wordt dat een foton op banden verder van het middelpunt terechtkomt. We weten dus zeker dat de banden in het centrum het helderst zijn en verder weg steeds zwakker worden. Maar we weten nooit zeker welk foton in welke band terechtkomt.
Een van de vreemde conclusies van de kwantummechanica theorie is het "Schrödinger's kat" effect. Over bepaalde eigenschappen van een deeltje, zoals hun positie, bewegingssnelheid, bewegingsrichting en "spin", kan pas worden gesproken als iets ze meet (een foton dat op een elektron afketst, zou bijvoorbeeld gelden als een meting van zijn positie). Vóór de meting bevindt het deeltje zich in een "superpositie van toestanden", waarin zijn eigenschappen vele waarden tegelijk hebben. Schrödinger zei dat de kwantummechanica leek te zeggen dat als iets (zoals het leven of de dood van een kat) werd bepaald door een kwantumgebeurtenis, de toestand ervan zou worden bepaald door de toestand die voortvloeide uit de kwantumgebeurtenis, maar alleen op het moment dat iemand naar de toestand van de kwantumgebeurtenis keek. In de tijd voordat naar de toestand van de kwantumgebeurtenis wordt gekeken, worden misschien "de levende en de dode kat (vergeef me de uitdrukking) in gelijke delen gemengd of uitgesmeerd".
Gereduceerde constante van Planck
Men gebruikt vaak het symbool ℏ 

Voorbeeld
Het deeltje in een 1-dimensionale put is het eenvoudigste voorbeeld dat aantoont dat de energie van een deeltje alleen specifieke waarden kan hebben. Men zegt dat de energie "gekwantificeerd" is. De put heeft nul potentiële energie binnen een bereik en heeft oneindig veel potentiële energie overal buiten dat bereik. Voor het eendimensionale geval in de richting 
Met behulp van differentiaalvergelijkingen kunnen we uitrekenen dat ψ
of als

De wanden van de doos betekenen dat de golffunctie een speciale vorm moet hebben. De golffunctie van het deeltje moet nul zijn wanneer de wanden oneindig lang zijn. Bij elke wand:
Beschouw x = 0
- sin 0 = 0, cos 0 = 1. Om te voldoen aan ψ
de cos term verwijderd worden. Dus D = 0
Beschouw nu:
- bij
ψ
- Als
dan is ψ
voor alle x. Deze oplossing is niet bruikbaar.
- daarom moet
waar zijn, wat ons het volgende oplevert
We kunnen zien dat 
Gerelateerde pagina's
- Elektromagnetische golf
- Elektron
- Foton
- Kwantumverstrengeling
- Kwantumcomputer
- Kwantumtoestand
- Schrödingervergelijking
Meer lezen
- Cox, Brian; & Forshaw, Jeff (2011). Het Kwantum Universum: Everything That Can Happen Does Happen. Allen Lane. ISBN 978-1-84614-432-5
Vragen en antwoorden
V: Wat is kwantummechanica?
A: Kwantummechanica is een tak van de natuurkunde die verklaart hoe het universum werkt op een schaal kleiner dan atomen. Het staat ook bekend als kwantumfysica of kwantumtheorie.
V: Wat betekent de term "kwantum"?
A: De term "kwantum" komt uit het Latijn en betekent "hoeveel". Een kwantum van energie is de kleinst mogelijke hoeveelheid (of de minst extra hoeveelheid), en de kwantummechanica beschrijft hoe die energie beweegt of op elkaar inwerkt.
V: Wat zijn subatomaire deeltjes?
A: Subatomaire deeltjes zijn deeltjes waaruit atomen bestaan, zoals protonen, neutronen en elektronen. Ze zijn nog kleiner dan atomen.
V: Hoe beschrijft de kwantummechanica hoe deze deeltjes werken?
A: De kwantummechanica biedt wiskundige regels om subatomaire deeltjes en elektromagnetische golven te bestuderen en zo hun gedrag en onderlinge interacties te begrijpen.
V: Wat is golf-deeltje dualiteit?
A: Golf-deeltjes dualiteit verwijst naar het feit dat zowel deeltjes als golven zich als elkaar kunnen gedragen - het zijn niet twee afzonderlijke entiteiten, maar eerder iets als beide gecombineerd in één fenomeen.
V: Hoe kan de moderne fysica worden beschreven met behulp van de kwantummechanica?
A: De moderne fysica en chemie kunnen worden verklaard door de wiskundige regels van de kwantummechanica erop toe te passen.
Zoek in de encyclopedie









