Exponentiële functie | functie die steeds sneller groeit
In de wiskunde is de exponentiële functie een functie die steeds sneller groeit. Het is de functie 
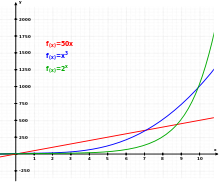
Drie verschillende functies: Lineair (rood), kubisch (blauw) en exponentieel (groen).
Eigenschappen
Omdat exponentiële functies exponentia gebruiken, volgen zij dezelfde exponentregels. Dus,

Dit volgt uit de regel dat 
De natuurlijke logaritme is de inverse bewerking van een exponentiële functie, waarbij:
De exponentiële functie voldoet aan een interessante en belangrijke eigenschap in de differentiaalrekening:
Dit betekent dat de helling van de exponentiële functie de exponentiële functie zelf is, en bijgevolg een helling van 1 heeft bij 
Toepassingen
De algemene exponentiële functie, waarbij de basis niet noodzakelijkerwijs 
Een voorbeeld van een exponentiële functie in het echte leven is de rente op een bank. Als iemand £100 stort op een rekening die elke maand 3% rente krijgt, dan zou het saldo elke maand (in de veronderstelling dat het geld onaangeroerd blijft) als volgt zijn:
| Maand | Balans | Maand | Balans |
| Januari | £100.00 | Juli | £119.41 |
| Februari | £103.00 | Augustus | £122.99 |
| Maart | £106.09 | September | £126.68 |
| April | £109.27 | Oktober | £130.48 |
| Mei | £112.55 | November | £134.39 |
| Juni | £115.93 | December | £138.42 |
Merk hier op hoe het extra geld uit rente elke maand toeneemt, in die zin dat hoe groter het oorspronkelijke saldo, hoe meer rente de persoon krijgt.
Hieronder staan twee wiskundige voorbeelden van exponentiële functies (met basis a).
| a=2
| a=3
|
Verband met de wiskundige constante e
Ook al kan de basis (
Het getal e is belangrijk voor elke exponentiële functie. Een bank betaalt bijvoorbeeld elke dag 0,01 procent rente. Iemand neemt zijn rentegeld en stopt het in een doos. Na 10.000 dagen (ongeveer 30 jaar) heeft hij 2 keer zoveel geld als waarmee hij begon. Een andere persoon neemt zijn rentegeld en stopt het terug in de bank. Omdat de bank hem nu rente betaalt over zijn rente, is de hoeveelheid geld een exponentiële functie.
In feite heeft hij na 10.000 dagen niet 2 keer zoveel geld als waarmee hij begon, maar wel 2,718145 keer zoveel geld als waarmee hij begon. Dit getal ligt heel dicht bij het getal e. Als de bank vaker rente betaalt, zodat het bedrag dat elke keer wordt betaald minder is, dan zal het getal dichter bij het getal e liggen.
Iemand kan ook naar de afbeelding kijken om te zien waarom het getal e belangrijk is voor exponentiële functies. De afbeelding bevat drie verschillende krommen. De curve met de zwarte punten is een exponentiële functie met een basis iets kleiner dan e. De curve met de korte zwarte lijnen is een exponentiële functie met een basis iets groter dan e. De blauwe curve is een exponentiële functie met een basis precies gelijk aan e. De rode lijn is een raaklijn aan de blauwe curve. Zij raakt de blauwe kromme op één punt zonder deze te kruisen. Men kan zien dat de rode curve de x-as kruist, de lijn die van links naar rechts gaat bij -1. Dit geldt alleen voor de blauwe curve. Dit is de reden dat de exponentiële functie met als basis e bijzonder is.
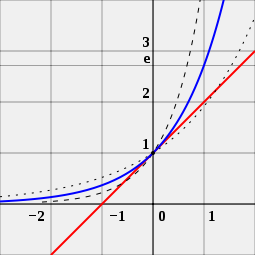
e is het unieke getal a, zodanig dat de waarde van de afgeleide van de exponentiële functie f (x) = ax (blauwe kromme) in het punt x = 0 precies 1 is. Ter vergelijking worden de functies 2x (gestippelde curve) en 4x (gestippelde curve) getoond; zij raken niet aan de lijn met helling 1 (rood).
Gerelateerde pagina's
Vragen en antwoorden
V: Wat is de exponentiële functie?
A: De exponentiële functie is een wiskundige functie die steeds sneller groeit.
V: Hoe wordt de exponentiële functie wiskundig uitgedrukt?
A: De exponentiële functie wordt wiskundig uitgedrukt als exp(x) = e^x, waarbij e de constante van Euler is.
V: Wat stelt de constante van Euler voor?
A: De constante van Euler staat voor een irrationeel getal dat ongeveer 2,71828 is.
V: Is de exponentiële functie altijd stijgend?
A: Ja, de exponentiële functie neemt altijd in waarde toe als x toeneemt.
V: Is er een grens aan hoe snel de exponentiële functie kan groeien?
A: Nee, er is geen limiet aan hoe snel de exponentiële functie kan groeien, omdat deze bij grotere waarden van x blijft toenemen.
V: Hoe kunnen wij de constante van Euler berekenen?
A: Wij kunnen de constante van Euler berekenen met numerieke methoden zoals Taylorreeksen of voortgezette breuken.
V: Welke andere toepassingen kent de exponentiële functie naast wiskunde?
A: De exponentiële functie heeft vele toepassingen buiten de wiskunde, waaronder natuurkunde, scheikunde, biologie, economie en techniek.
Zoek in de encyclopedie


