Differentiaalrekening | de studie van het vinden van de veranderingssnelheid van een variabele

Achtergrond

In tegenstelling tot een getal zoals 5 of 200, kan een variabele zijn waarde veranderen. Afstand en tijd zijn bijvoorbeeld variabelen. Bij een Olympische hardloopwedstrijd gaat de afstand vanaf de startlijn omhoog naarmate de persoon loopt. Ondertussen meet een stopwatch of klok de tijd die omhoog gaat. Wij kunnen de gemiddelde snelheid van de loper meten door de afgelegde afstand te delen door de tijd. Maar dit zegt niet met welke snelheid de persoon precies 1,5 seconde in de race liep. Als we de afstand op 1 seconde hadden en de afstand op 2 seconden, zouden we nog steeds slechts een gemiddelde hebben, hoewel het waarschijnlijk correcter zou zijn dan het gemiddelde voor de hele race.

Totdat de calculus werd uitgevonden, was de enige manier om dit uit te rekenen de tijd in steeds kleinere stukjes te knippen, zodat de gemiddelde snelheid over de kleinere tijd steeds dichter bij de werkelijke snelheid op precies 1,5 seconden zou komen. Dit was een zeer lang en moeilijk proces, en moest telkens worden gedaan als men iets wilde uitrekenen. Het is zeker veel moeilijker voor een bestuurder om de snelheid van een auto te achterhalen door alleen de kilometerteller (afstandsmeter) en de klok te gebruiken - zonder snelheidsmeter.

Een zeer vergelijkbaar probleem is het vinden van de helling (hoe steil deze is) op een willekeurig punt van een kromme. De helling van een rechte lijn is gemakkelijk uit te rekenen - het is gewoon hoeveel hij omhoog gaat (y of verticaal) gedeeld door hoeveel hij overdwars gaat (x of horizontaal). Als een lijn evenwijdig is aan de x-as, dan is de helling nul. Als een rechte lijn gaat door (x,y) = (2,10) en (4,18), dan gaat de lijn 8 omhoog en 2 over, dus de helling is 8 gedeeld door 2, wat 4 is.

Op een "kromme" is de helling echter variabel (heeft verschillende waarden op verschillende punten), omdat de lijn buigt. Maar als de kromme in zeer, zeer kleine stukjes zou worden gesneden, zou de kromme in het punt er bijna uitzien als een zeer korte rechte lijn. Dus om de helling te berekenen, kan een rechte lijn worden getrokken door het punt met dezelfde helling als de kromme in dat punt. Als dit precies goed wordt gedaan, zal de rechte lijn dezelfde helling hebben als de kromme, en wordt deze een raaklijn genoemd. Maar er is geen manier om te weten (zonder berekening) of de raaklijn precies goed is, en onze ogen zijn niet nauwkeurig genoeg om zeker te weten of hij precies is of er gewoon heel dicht bij ligt.

Wat Newton en Leibniz vonden was een manier om de helling (of de snelheid in het voorbeeld van de afstand) exact uit te rekenen, met behulp van eenvoudige en logische regels. Zij verdeelden de kromme in een oneindig aantal zeer kleine stukjes. Zij kozen vervolgens punten aan weerszijden van het punt waarin zij geïnteresseerd waren en berekenden raaklijnen bij elk punt. Naarmate de punten dichter bij elkaar kwamen naar het punt waarin zij geïnteresseerd waren, naderde de helling een bepaalde waarde naarmate de raaklijnen de werkelijke helling van de kromme naderden. Zij zeiden dat deze specifieke waarde die zij benaderden de werkelijke helling was.

 
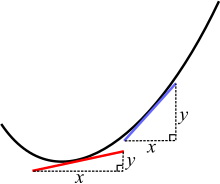
Op een kromme hebben twee verschillende punten verschillende hellingen. De rode en blauwe lijnen zijn raaklijnen aan de kromme.  

Hoe het werkt

Laten we zeggen dat we een functie hebben y = f(x). f is een afkorting voor functie, dus deze vergelijking betekent "y is een functie van x". Dit vertelt ons dat hoe hoog y op de verticale as staat, afhangt van wat x (de horizontale as) op dat moment is. Bijvoorbeeld, met de vergelijking y = x² weten we dat als x 1 is, y 1 zal zijn; als x 3 is, y 9 zal zijn; als x 20 is, y 400 zal zijn.

Kies een punt A op de kromme, en noem zijn horizontale positie x. Kies dan een ander punt B op de kromme dat iets verder ligt dan A, en noem zijn horizontale positie x + h. Het maakt niet uit hoeveel h is; het is een heel klein getal.

Dus als we van punt A naar punt B gaan, is de verticale positie van f(x) naar f(x + h) gegaan, en de horizontale positie van x naar x + h. Onthoud dat de helling is hoeveel hij omhoog gaat gedeeld door hoeveel hij overgaat. Dus de helling is:

f ( x + h ) - f ( x ) h {frac {f(x+h)-f(x)}{h}}.

Als u B steeds dichter bij A brengt - wat betekent dat h steeds dichter bij 0 komt - dan komen we dichter bij de vraag wat de helling is in het punt A.

lim h → 0 f ( x + h ) - f ( x ) h {{displaystyle}lim _{hrightarrow 0}{frac {f(x+h)-f(x)}{h}}.

Laten we nu teruggaan naar y = x². De helling hiervan kan als volgt worden bepaald:

= lim h → 0 f ( x + h ) - f ( x ) h = lim h → 0 ( x + h ) 2 - ( x ) 2 h {displaystyle {begin{aligned}&==lim _{hrightarrow 0}{frac {f(x+h)-f(x)}{h}}&=lim _{hrightarrow 0}{frac {(x+h)^{2}-(x)^{2}{h}}}end{aligned}}}.

Door toepassing van het binomiaal theorema dat onder andere stelt dat ( x + y ) 2 = x 2 + 2 x y + y 2 {{displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}} kunnen we de uitdrukking reduceren tot:

= lim h → 0 x 2 + 2 x h + h 2 - x 2 h = lim h → 0 2 x h + h 2 h = lim h → 0 2 x + h = 2 x {displaystyle {begin{aligned}&==lim _{hrightarrow 0}{{frac {x^{2}+2xh+h^{2}-x^{2}}{h}}&=lim _{hrightarrow 0}{{frac {2xh+h^{2}}{h}}&=lim _{hrightarrow 0}2x+h}&={frac {}}2x{aligned}}}.

We weten dus zonder raaklijnen te hoeven tekenen dat op elk punt van de kromme f(x) = x², de afgeleide f'(x) (gemarkeerd met een apostrof) 2x zal zijn. Dit proces van het berekenen van een helling met behulp van limieten heet differentiëren, of het vinden van de afgeleide.

Leibniz kwam tot hetzelfde resultaat, maar noemde h "dx", wat betekent "een kleine hoeveelheid x". De resulterende verandering in f(x) noemde hij "dy", wat "een heel klein beetje y" betekent. De notatie van Leibniz wordt in meer boeken gebruikt omdat deze gemakkelijk te begrijpen is, wanneer de vergelijkingen ingewikkelder worden. In de notatie van Leibniz:

d y d x = f ′ ( x ) {displaystyle {frac {dy}{dx}}=f'(x)}

 
Een plaatje dat laat zien wat x en x + h betekenen op de kromme.  

Regels

Met behulp van het bovenstaande systeem hebben wiskundigen regels opgesteld die altijd werken, ongeacht welke functie wordt bekeken. (Opmerking: hier zijn u en v beide functies van x ).

Voorwaarde	Functie	Afgeleide	Voorbeeld	Afgeleide
Een getal op zich	y = a {displaystyle y=a}	d y d x = 0 {displaystyle {frac {dy}{dx}}=0}	y = 3 {displaystyle y=3}	0 {displaystyle 0}
Een rechte lijn	y = m x + c {displaystyle y=mx+c}	d y d x = m {frac {dy}{dx}}=m}	y = 3 x + 5 {displaystyle y=3x+5}	3 {displaystyle 3}
x tot de macht van een getal	x a {{a}}	d y d x = a x a - 1 {displaystyle {frac {dy}{dx}}=ax^{a-1}}	x 12 {{12}}	12 x 11 {Displaystyle 12x^{11}}
Een getal vermenigvuldigd met een functie	y = c ⋅ u {displaystyle y=ccdot u}	d y d x = c d u d x {displaystyle {frac {dy}{dx}}=c{frac {du}{dx}}}	y = 3 ( x 2 + x ) {\displaystyle y=3(x^{2}+x)}	3 ( 2 x + 1 ) {\displaystyle 3(2x+1)}
Een functie plus een andere functie	y = u + v {displaystyle y=u+v}	d y d x = d u d x + d v d x {{displaystyle {frac {dy}{dx}}={frac {du}{dx}}+{frac {dv}{dx}}}	y = 3 x 2 + x {\displaystyle y=3x^{2}+{{sqrt {x}}}	6 x + 1 2 x {\frac {1}{2{sqrt {x}}}}}
Een functie min een andere functie	y = u - v {displaystyle y=u-v}	d y d x = d u d x - d v d x {displaystyle {frac {dy}{dx}}={frac {du}{dx}}-{frac {dv}{dx}}}	y = 3 x 2 - x {\displaystyle y=3x^{2}-{\sqrt {x}}}	6 x - 1 2 x {\frac {1}{2{sqrt {x}}}}}
Productregel  Een functie vermenigvuldigd met een andere functie	y = u ⋅ v {displaystyle y=u}	d y d x = d u d x v + u d v d x {{displaystyle {frac {dy}{dx}}={frac {du}{dx}}v+u{frac {dv}{dx}}}}	y = ( x 2 + x + 2 ) ( 3 x - 1 ) {\displaystyle y=(x^{2}+x+2)(3x-1)}	( 3 x - 1 ) ( 2 x + 1 ) + 3 ( x 2 + x + 2 ) {{displaystyle (3x-1)(2x+1)+3(x^{2}+x+2)}
Quotiëntregel  Een functie gedeeld door een andere functie	y = u v {{displaystyle y={frac {u}{v}}}	d y d x = d u d x v - u d v d x v 2 {\displaystyle {frac {dy}{dx}}={{frac {du}{dx}}v-u{{frac {dv}{dx}}}{v^{2}}}}	y = x 2 + 2 x - 1 {\displaystyle y={frac {x^{2}+2}{x-1}}}	2 x ( x - 1 ) - ( x 2 + 2 ) ( x - 1 ) 2 {frac {2x(x-1)-(x^{2}+2)}{(x-1)^{2}}}}
Kettingregel  Gebruikt voor samengestelde functies	y = u ∘ v {displaystyle y=u}	d y d x = d y d u ⋅ d u d x {displaystyle {dy}{dx}}={frac {dy}{du}}cdot {frac {du}{dx}}}	y = 2 x - 1 {displaystyle y={{sqrt {2x-1}}}	2 2 x - 1 = 1 2 x - 1 {displaystyle {frac {2}{2{sqrt {2x-1}}}}={frac {1}{sqrt {2x-1}}}}
Een exponentiële functie	y = e x {{}}y=e^{x}}}	d y d x = e x {frac {dy}{dx}}=e^{x}}	y = e x {{}}y=e^{x}}}	e x {frac {}{}}e^{x}}

 

Gerelateerde pagina's

• Afgeleide (wiskunde)
• Differentiële operator
• Gewone differentiaalvergelijking
• Wiskundige analyse