Gumbel verdeling
De Gumbel-verdeling is een kansverdeling van extreme waarden.
In de kansrekening en de statistiek wordt de Gumbel-verdeling gebruikt om de verdeling van het maximum (of het minimum) van een aantal steekproeven van verschillende verdelingen te modelleren.
Een dergelijke verdeling kan worden gebruikt om de verdeling van het maximumniveau van een rivier in een bepaald jaar weer te geven als er een lijst van maximumwaarden voor de afgelopen tien jaar bestaat. Het is ook nuttig om de kans op een extreme aardbeving, overstroming of andere natuurramp te voorspellen.
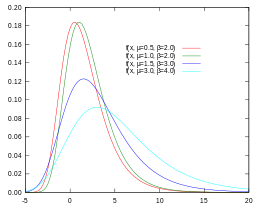
Gumbel kansverdelingsfunctie (PDF)
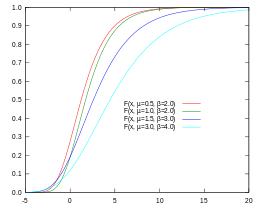
Gumbel cumulatieve verdelingsfunctie (CDF)
Eigenschappen
De Gumbel-verdeling is een continue kansverdeling. Gumbel-verdelingen zijn een familie van verdelingen met dezelfde algemene vorm. Deze verdelingen verschillen in hun plaats- en schaalparameters: het gemiddelde ("gemiddelde") van de verdeling bepaalt de plaats, en de standaardafwijking ("variabiliteit") bepaalt de schaal.
Men herkent de Gumbel kansdichtheidsfunctie (PDF) en de Gumbel cumulatieve verdelingsfunctie (CDF).
In de PDF wordt de waarschijnlijkheid P van een waarde V tussen de grenzen A en B, kortweg geschreven als P(A<V<B), gevonden door het gebied onder de PDF-curve tussen A en B.
| Voorbeeld van waarschijnlijkheid in de PDF |
| In de figuur van de normale kansdichtheidsfunctie moeten de waarden op de horizontale as respectievelijk luiden: μ-3σ, μ-2σ, μ-1σ, μ+1σ, μ+2σ, en μ+3σ. μ = gemiddelde, σ = standaardafwijking. |
In tegenstelling tot de normale verdeling is de Gumbel-PDF a-symmetrisch en scheef naar rechts.
CDF
In de CDF wordt de kans dat een waarde V kleiner is dan A direct gevonden als de CDF-waarde bij A:
P ( V ≤ A ) = C D F ( A ) {P(V ≤ A)=CDF(A)}
| Voorbeeld van waarschijnlijkheid in de CDF |
| In de Gumbel CDF-figuur geeft de rode curve aan dat de kans dat V kleiner is dan 5 0,9 (of 90%) is, terwijl die kans voor de donkerblauwe lijn 0,7 of 70% is. |

De normale waarschijnlijkheidsdichtheidsfunctie (PDF) is symmetrisch.
Wiskunde
De CDF
De wiskundige uitdrukking van de CDF is:
C D F ( A ) = e - e - ( A - μ ) / β , {Displaystyle CDF(A)=e^{-e^{-(A -mu )/\beta },}.
waarin μ de modus is (de waarde waar de kansdichtheidsfunctie zijn piek bereikt), e een wiskundige constante, ongeveer 2,718, en β een waarde die verband houdt met de standaardafwijking (σ) :
β = σ 6 / π , {\beta = \sigma {sqrt {6}} / π , }
waarbij π het Griekse symbool voor Pi is, waarvan de waarde dicht bij 22/7 of 3,142 ligt, en het symbool {{displaystyle}}
Modus en mediaan
De modus μ kan worden gevonden uit de mediaan M, zijnde de waarde van A waarbij CDF(A)=0,5, en β:
μ = M + β ln ( ln 2 ) , {Displaystyle \mu =M+\beta \ln \left(\ln 2\right),}.
waarbij ln de natuurlijke logaritme is.
Gemiddelde
Het gemiddelde, E(x), gegeven door:
E ( x ) = μ + c β , {displaystyle {E} (x)= μ + c β , }
waarbij c

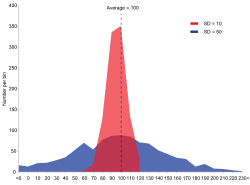
Er zijn twee gegevensreeksen: rood en blauw. Beide hebben hetzelfde gemiddelde: 100, maar de blauwe groep heeft een grotere standaardafwijking (SD=σ=50) dan de rode groep (SD=σ=10).
Schatting
In een gegevensreeks kunnen de parameters modus (μ) en β worden geschat uit het gemiddelde, de mediaan en de standaardafwijking. De berekening van de laatste drie grootheden wordt uitgelegd in de respectieve Wiki-pagina's. Vervolgens kunnen met behulp van de in het vorige hoofdstuk gegeven formules de factoren μ en β worden berekend. Zo kan de CDF van de bij de gegevens behorende Gumbel-verdeling worden bepaald en kan de waarschijnlijkheid van interessante gegevenswaarden worden gevonden.

Cumulatieve Gumbel-verdeling van de maximale eendaagse regenval in oktober met behulp van CumFreq
Toepassing
In de hydrologie wordt de Gumbel-verdeling gebruikt voor het analyseren van variabelen als maandelijkse en jaarlijkse maximumwaarden van dagelijkse neerslag en rivierafvoer, en ook voor het beschrijven van droogteperioden.
De blauwe afbeelding illustreert een voorbeeld van de aanpassing van de Gumbel-verdeling aan de gerangschikte maximale eendaagse regenval in oktober, waarbij ook de 90%-betrouwbaarheidsgordel op basis van de binomiale verdeling wordt getoond.
Vragen en antwoorden
V: Wat is de Gumbel-verdeling?
A: De Gumbel-verdeling is een kansverdeling van extreme waarden.
V: Waarvoor wordt de Gumbel-verdeling gebruikt?
A: De Gumbel-verdeling wordt gebruikt om de verdeling van het maximum (of minimum) van een aantal steekproeven van verschillende verdelingen te modelleren.
V: Hoe kan de Gumbel-verdeling gebruikt worden bij het voorspellen van natuurrampen?
A: De Gumbel-verdeling is nuttig bij het voorspellen van de kans dat een extreme aardbeving, overstroming of andere natuurramp zal plaatsvinden.
V: Wat is een voorbeeld van het gebruik van de Gumbel-verdeling om een gebeurtenis uit het verleden weer te geven?
A: De Gumbel-verdeling zou gebruikt kunnen worden om de verdeling van het maximumniveau van een rivier in een bepaald jaar weer te geven als er een lijst met maximumwaarden van de afgelopen tien jaar was.
V: Is de Gumbel-verdeling alleen nuttig bij het voorspellen van natuurrampen?
A: Nee, de Gumbel-verdeling kan gebruikt worden om de verdeling van extreme waarden in elke situatie te modelleren.
V: Kan de Gumbel-verdeling worden gebruikt om de minimumwaarde van een reeks steekproeven te modelleren?
A: Ja, de Gumbel-verdeling kan worden gebruikt om de verdeling van zowel het maximum als het minimum van een verzameling steekproeven te modelleren.
V: Is de Gumbel-verdeling een veelgebruikte verdeling in de kansrekening en statistiek?
A: Ja, de Gumbel-verdeling is een veelgebruikte verdeling in de kansrekening en statistiek, vooral voor het modelleren van extreme waarden.
Zoek in de encyclopedie



