Logaritmische schaal
Een logaritmische schaal is een schaal die wordt gebruikt wanneer er een groot scala aan hoeveelheden is. Veelgebruikte toepassingen zijn onder andere aardbevingssterkte, geluidssterkte, lichtintensiteit en pH van oplossingen.
Het is gebaseerd op orden van grootte, in plaats van een standaard lineaire schaal. De waarde van elk merkteken op de schaal is de waarde bij het vorige merkteken vermenigvuldigd met een constante.
Logaritmische schalen worden ook gebruikt in rekenlinialen voor het vermenigvuldigen of delen van getallen door het optellen of aftrekken van lengtes op de schalen.
De logaritmische schaal kan nuttig zijn wanneer de gegevens een groot bereik van waarden bestrijken - het logaritme reduceert dit tot een beter beheersbaar bereik.
Sommige van onze zintuigen werken op een logaritmische manier (het vermenigvuldigen van de werkelijke ingangssterkte voegt een constante toe aan de waargenomen signaalsterkte, zie: Stevens' machtswet). Dat maakt logaritmische schalen voor deze ingangshoeveelheden bijzonder geschikt. Met name ons gehoor neemt gelijke veelvouden van frequenties als gelijke verschillen in toonhoogte waar.
Op de meeste logaritmische schalen komen kleine veelvouden (of verhoudingen) van de onderliggende hoeveelheid overeen met kleine (mogelijk negatieve) waarden van de logaritmische maat.
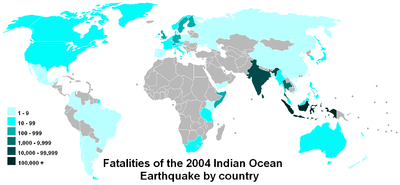
Een logboek schaal maakt het gemakkelijk om waarden te vergelijken die een groot bereik bestrijken, zoals in deze kaart
De twee logaritmische schalen van een rekenliniaal
Voorbeelden
Bekende voorbeelden van dergelijke schalen zijn:
- Richter magnitudeschaal en momentmagnitudeschaal (MMS) voor sterkte van aardbevingen en beweging in de aarde.
- bel en decibel en neper voor akoestisch vermogen (luidheid) en elektrisch vermogen;
- het tellen van f-stops voor ratio's van de fotografische belichting;
- de beoordeling van lage waarschijnlijkheden met het aantal 'negens' in de decimale uitbreiding van de kans dat ze niet gebeuren: een systeem dat bijvoorbeeld met een kans van 10-5 faalt, is 99,999% betrouwbaar: "vijf negens".
- Entropie in de thermodynamica.
- Informatie in de informatietheorie.
- Deeltjesgrootteverdeelcurven van de bodem
Sommige logaritmische schalen zijn zo ontworpen dat grote waarden (of verhoudingen) van de onderliggende hoeveelheid overeenkomen met kleine waarden van de logaritmische maat. Voorbeelden van dergelijke schalen zijn:
- pH voor de zuurgraad;
- stellaire magnitudeschaal voor de helderheid van sterren;
Een logaritmische schaal is ook een grafische schaal op één of beide zijden van een grafiek waarbij een getal x op een afstand c-log(x) van het met het getal 1 gemarkeerde punt is afgedrukt. Een rekenliniaal heeft logaritmische schalen, en nomogrammen maken vaak gebruik van logaritmische schalen. Op een logaritmische schaal wordt een gelijk verschil in orde van grootte weergegeven door een gelijke afstand. Het meetkundig gemiddelde van twee getallen ligt halverwege de getallen.
Logaritmisch grafiekpapier was vóór de komst van de computergrafiek een wetenschappelijk basisinstrument. Plots op papier met één logschaal kunnen exponentiële wetten laten zien, en op log-log-papieren machtswetten, als rechte lijnen (zie semilogische grafiek, log-log-grafiek).
Vragen en antwoorden
V: Wat is een logaritmische schaal?
A: Een logaritmische schaal is een schaal die gebruikt wordt bij grote hoeveelheden.
V: Wat zijn enkele voorbeelden van dingen die op een logaritmische schaal gemeten kunnen worden?
A: De sterkte van aardbevingen, de luidheid van geluid, de intensiteit van licht, de verspreidingssnelheid van epidemieën en de pH van oplossingen kunnen allemaal op een logaritmische schaal gemeten worden.
V: Waarin verschilt een logaritmische schaal van een standaard lineaire schaal?
A: Een logaritmische schaal is gebaseerd op orden van grootte, in plaats van een standaard lineaire schaal. De waarde van elk merkteken op de schaal is de waarde bij het vorige merkteken vermenigvuldigd met een constante.
V: Wat is het voordeel van het gebruik van een logaritmische schaal?
A: De logaritmische schaal kan een groot bereik aan waarden reduceren tot een beter hanteerbaar bereik, wat handig kan zijn bij gegevens die een groot bereik aan waarden hebben.
V: Wat is de machtswet van Stevens en hoe houdt deze wet verband met logaritmische schalen?
A: De machtswet van Stevens beschrijft hoe sommige van onze zintuigen logaritmisch werken, waarbij het vermenigvuldigen van de werkelijke ingangssterkte een constante toevoegt aan de waargenomen signaalsterkte. Dit maakt logaritmische schalen voor deze ingangsgrootheden bijzonder geschikt.
V: Waarom is een logaritmische schaal bijzonder nuttig voor het meten van de luidheid van geluid?
A: Ons gehoor neemt gelijke veelvouden van frequenties waar als gelijke verschillen in toonhoogte, dus een logaritmische schaal kan deze relatie tussen geluidsfrequentie en waargenomen luidheid nauwkeurig weergeven.
V: Wat is de relatie tussen kleine veelvouden van de onderliggende grootheid en de logaritmische maat op de meeste logaritmische schalen?
A: Op de meeste logaritmische schalen komen kleine veelvouden (of ratio's) van de onderliggende grootheid overeen met kleine (mogelijk negatieve) waarden van de logaritmische maat.
Zoek in de encyclopedie